1 概率论基础
本福特定律(第一数字定律):在实际生活中得出的一组数据中,以1为首位数字出现的概率约为总数的三成。
条件概率
全概率公式
贝叶斯公式
给定某系统的若干样本,计算该系统的参数,即:
P(θ):先验概率,没有数据支持下,θ发生的概率
P(θ|X) :后验概率,在数据x支持下θ发生的概率
P(X|θ):给定某参数θ的概率分布,似然函数
2 常见概率分布
|
分布 |
参数 |
数学期望 |
方差 |
|
两点分布 |
0<p<1 |
p |
p(1-p) |
|
二项分布 |
n>=1,0<p<1 |
np |
np(1-p) |
|
泊松分布 |
γ>0 |
γ |
γ |
|
均匀分布 |
a<b |
(a+b)/2 |
(b-a)2/12 |
|
指数分布 |
θ>0 |
θ |
θ2 |
|
正态分布 |
μ, σ>0 |
μ |
σ2 |
3 统计量
3.1 期望
离散型:
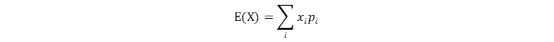
连续型:
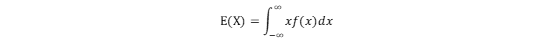
期望的性质:
无条件成立关系式:
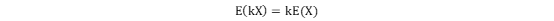
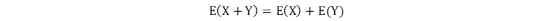
若X和Y相互独立:E(XY)=E(X)E(Y),反之不成立,只能说明X和Y不相关
3.2 方差
定义:Var(X)=E{[X-E(X)]2}=E(X2)-E2(X)
方差的性质:
无条件成立关系式:Var(c)=0
Var(X+c)=Var(X)
Var(kX)=k2Var(X)
若X和Y相互独立:Var(X+Y)=Var(X)+Var(Y)
3.3 协方差
定义:Cov(X,Y)=E{[X-E(X)][Y-E(Y)]}
性质:
Cov(X,Y)=Cov(Y,X)
Cov(aX+b,cY+d)=acCov(X,Y)
Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)
Cov(X,Y)=E(XY)-E(X)E(Y)
3.4 相关系数
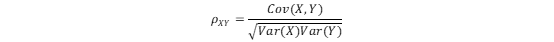
4 独立
给定A和B是两个事件,若有P(AB)=P(A)P(B),则称事件A和B相互独立。
5 大数定律
设随机变量X1,X2,…Xn互相独立,并且具有相同的期望μ和方差σ2。作前n个随机变量的平均Yn,则对于任意正数ε,有:
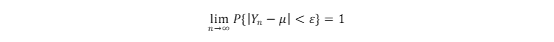
6 中心极限定理
设随机变量X1,X2,…Xn互相独立,服从同一分布,并且具有相同的期望μ和方差σ2,则随机变量:
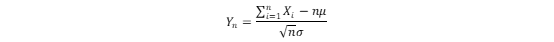
的分布收敛到标准正态分布。