一、问题描述

输入一组整数，求出这个整数数组最大和的连续子串。例如，整数数组为{4, -2, 59, -45, 4}，最大和的连续子串为{4, -2, 59}，最大和为61。需要注意的是要求子串连续，另外，子串的长度可以是1.

这个也是曾经出过的一道面试提，最早是浙大的一道考研算法设计题。

二、问题分析

第一种方法。最简单的思路就是用两层循环来解决问题。外面一层是从1到整数数组的长度，里面的那层循环是当前的位置加1一直到整数数组的结束，里面的循环来算所有的和。换句话说就是，内层循环每次从i+1开始到字符数组结束的和，这些和是numbers[i]+numbers[i+1]，numbers[i]+numbers[i+1]+numbers[i+2]，...，numbers[i]+...+numbers[length(numbers)]中找到最大的那个。外层循环则是找到全局最大的那个。这个方法比较好想，只给出伪代码，这个的时间复杂度为：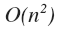

下面是伪代码：

for i = 0 to length(numbers)
   current = numbers[i]
   for j = i + 1 to length(numbers)
      current += numbers[j]
      if(current_max < current)
         current_max = current
    end
    if(max < current_max)
    max = current_max
end

第二种思路可以设置一个变量current_max来保存当前作出的最大和，用一个变量max来保存全局的最大和。当加到一个负数时，当前和会减少，但是，是不是会不会改变全局最大和还需要看后面的一个元素。而如果当前的current_max变为负数了，说明如果再用这个数加后面的数只会使和变小，所以把current_max赋值为0，但是需要额外考虑的就是数组全为负数的情况。用这种方法可以把时间复杂度降到O(n)。

第三种思路可以考虑动态规划的方法，但是用动态规划解决问题的思路我还没有弄的太明白，等弄明白后在补充到这里。

三、程序实现

#include <stdio.h>
#include <stdlib.h>

#define MAX(a, b) ((a)>(b)?(a):(b))

int main(int argc, char const *argv[])
{
	int n,
		i,
		current_max,
		max;
	int* numbers;

	printf("Please input the integer n(n > 0):\n");
	while(EOF != (scanf("%d", &n)))
	{
		numbers = (int*)malloc(n * sizeof(int));
		i = 0;

		while(i++ < n)
			scanf("%d", &numbers[i - 1]);

		printf("The computing numbers are : %d", numbers[0]);
		for(i = 1; i < n; i++)
			printf(",%d", numbers[i]);
		printf("\n");

		current_max = numbers[0];
		max = current_max;

		for(i = 1; i < n; i++)
		{
			current_max += numbers[i];
			max = MAX(max, current_max);
			max = MAX(max, numbers[i]);

			if(0 > current_max)
			{
				if((i + 1) != (n - 1))
					current_max = 0;
				else
					current_max = numbers[i];
			}
		}

		printf("the restult is : %d\n", max);

		free(numbers);

		printf("Please input the integer n(n > 0):\n");
	}

	return 0;
}

看计算时的那个for循环，我的思路是先进行相加在考虑是否改变current_max和max，还有一种思路是考虑利用上一次current_max的值来判断对current_max操作，即求和或者赋值为当前数组元素的值，之后在设置全局最大值max(见参考文献1)，这里给出这种情况求和的伪代码：

max=numbers[0];       
current_max=0;  
for(i=0;i<n;i++)  
{  
    if(current_max>=0)   
        current_max+=numbers[i];  
    else     
        current_max=numbers[i];  
    if(current_max>max)  
        max=current_max;  
}