EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计。
使用EM算法的原因
首先举李航老师《统计学习方法》中的例子来说明为什么要用EM算法估计含有隐变量的概率模型参数。
假设有三枚硬币,分别记作A, B, C。这些硬币正面出现的概率分别是$\pi,p,q$。进行如下掷硬币试验:先掷硬币A,根据其结果选出硬币B或C,正面选硬币B,反面边硬币C;然后掷选出的硬币,掷硬币的结果出现正面记作1,反面记作0;独立地重复$n$次试验,观测结果为$\{y_1,y_2,...,y_n\}$。问三硬币出现正面的概率。
三硬币模型(也就是第二枚硬币正反面的概率)可以写作
$ \begin{aligned} &P(y|\pi,p,q) \\ =&\sum\limits_z P(y,z|\pi,p,q)\\ =&\sum\limits_z P(y|z,\pi,p,q)P(z|\pi,p,q)\\ =&\pi p^y(1-p)^{1-y}+(1-\pi)q^y(1-q)^{1-y} \end{aligned} $
其中$z$表示硬币A的结果,也就是前面说的隐变量。通常我们直接使用极大似然估计,即最大化似然函数
$ \begin{aligned} &\max\limits_{\pi,p,q}\prod\limits_{i=1}^n P(y_i|\pi,p,q) \\ =&\max\limits_{\pi,p,q}\prod\limits_{i=1}^n[\pi p^{y_i}(1-p)^{1-y_i}+(1-\pi)q^{y_i}(1-q)^{1-y_i}]\\ =&\max\limits_{\pi,p,q}\sum\limits_{i=1}^n\log[\pi p^{y_i}(1-p)^{1-y_i}+(1-\pi)q^{y_i}(1-q)^{1-y_i}]\\ =&\max\limits_{\pi,p,q}L(\pi,p,q) \end{aligned} $
分别对$\pi,p,q$求偏导并等于0,求解线性方程组来估计这三个参数。但是,由于它是带有隐变量的,在获取最终的随机变量之前有一个分支选择的过程,导致这个$\log$的内部是加和的形式,计算导数十分困难,而待求解的方程组不是线性方程组。当复杂度一高,解这种方程组几乎成为不可能的事。以下推导EM算法,它以迭代的方式来求解这些参数,应该也算一种贪心吧。
算法导出与理解
对于参数为$\theta$且含有隐变量$Z$的概率模型,进行$n$次抽样。假设随机变量$Y$的观察值为$\mathcal{Y} = \{y_1,y_2,...,y_n\}$,隐变量$Z$的$m$个可能的取值为$\mathcal{Z}=\{z_1,z_2,...,z_m\}$。
写出似然函数:
$ \begin{aligned} L(\theta) &= \sum\limits_{Y\in\mathcal{Y}}\log P(Y|\theta)\\ &=\sum\limits_{Y\in\mathcal{Y}}\log \sum\limits_{Z\in \mathcal{Z}} P(Y,Z|\theta)\\ \end{aligned} $
EM算法首先初始化参数$\theta = \theta^0$,然后每一步迭代都会使似然函数增大,即$L(\theta^{k+1})\ge L(\theta^k)$。如何做到不断变大呢?考虑迭代前的似然函数(为了方便不用$\theta^{k+1}$):
$ \begin{gather} \begin{aligned} L(\theta)=&\sum\limits_{Y\in \mathcal{Y}} \log\sum\limits_{Z\in \mathcal{Z}} P(Y,Z|\theta)\\ =&\sum\limits_{Y\in \mathcal{Y}} \log\sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta^k)\frac{P(Y,Z|\theta)}{P(Z|Y,\theta^k)}\\ \end{aligned} \label{} \end{gather} $
至于上式的第二个等式为什么取出$P(Z|Y,\theta^k)$而不是别的,正向的原因我想不出来,马后炮原因在后面记录。
考虑其中的求和
$ \sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta^k)=1$
且由于$\log$函数是凹函数,因此由Jenson不等式得
$ \begin{gather} \begin{aligned} L(\theta) \ge&\sum\limits_{Y\in \mathcal{Y}}\sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta^k)\log\frac{P(Y,Z|\theta)}{P(Z|Y,\theta^k)}\\ =&B(\theta,\theta^k) \end{aligned}\label{} \end{gather} $
当$\theta = \theta^k$时,有
$ \begin{gather} \begin{aligned} L(\theta^k) \ge& B(\theta^k,\theta^k)\\ =&\sum\limits_{Y\in \mathcal{Y}}\sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta^k)\log\frac{P(Y,Z|\theta^k)}{P(Z|Y,\theta^k)}\\ =&\sum\limits_{Y\in \mathcal{Y}}\sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta^k)\log P(Y|\theta^k)\\ =&\sum\limits_{Y\in \mathcal{Y}}\log P(Y|\theta^k)\\ =&L(\theta^k)\\ \end{aligned} \label{} \end{gather} $
也就是在这时,$(2)$式取等,即$L(\theta^k) = B(\theta^k,\theta^k)$。取
$ \begin{gather} \theta^*=\text{arg}\max\limits_{\theta}B(\theta,\theta^k)\label{} \end{gather} $
可得不等式
$L(\theta^*)\ge B(\theta^*,\theta^k)\ge B(\theta^k,\theta^k) = L(\theta^k)$
所以,我们只要优化$(4)$式,让$\theta^{k+1} = \theta^*$,即可保证每次迭代的非递减势头,有$L(\theta^{k+1})\ge L(\theta^k)$。而由于似然函数是概率乘积的对数,一定有$L(\theta) < 0$,所以迭代有上界并且会收敛。以下是《统计学习方法》中EM算法一次迭代的示意图:
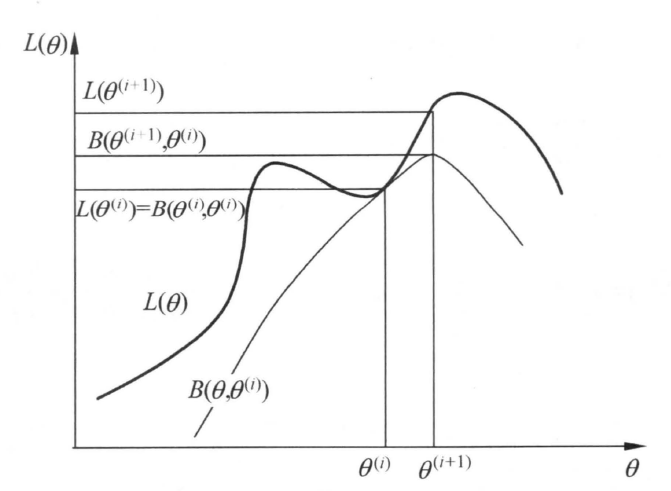
进一步简化$(4)$式,去掉优化无关项:
$ \begin{aligned} \theta^*=&\text{arg}\max\limits_{\theta}B(\theta,\theta^k) \\ =&\text{arg}\max\limits_{\theta}\sum\limits_{Y\in \mathcal{Y}}\sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta^k)\log\frac{P(Y,Z|\theta)}{P(Z|Y,\theta^k)} \\ =&\text{arg}\max\limits_{\theta}\sum\limits_{Y\in \mathcal{Y}}\sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta^k)\log P(Y,Z|\theta) \\ =&\text{arg}\max\limits_{\theta}Q(\theta,\theta^k) \\ \end{aligned} $
$Q$函数使用导数求极值的方程与没有隐变量的方程类似,容易求解。
综上,EM算法的流程为:
1. 设置$\theta^0$的初值。EM算法对初值是敏感的,不同初值迭代出来的结果可能不同。
2. 更新$\theta^k = \text{arg}\max\limits_{\theta}Q(\theta,\theta^{k-1})$。理解上来说,通常将这一步分为计算$Q$与极大化$Q$两步,即求期望E与求极大M,但在代码中并不会将它们分出来,因此这里浓缩为一步。另外,如果这个优化很难计算的话,因为有不等式的保证,直接取$\theta^k$为某个$\hat{\theta}$,只要有$Q(\hat{\theta},\theta^{k-1})\ge Q(\theta^{k-1},\theta^{k-1})$即可。
3. 比较$\theta^k$与$\theta^{k-1}$的差异,比如求它们的差的二范数,若小于一定阈值就结束迭代,否则重复步骤2。
下面记录一下我对$(1)$式取出$P(Z|Y,\theta^k)$而不取别的$P$的理解:
经过以上的推导,我认为这是为了给不等式取等创造条件。如果不能确定$L(\theta^k)$与$Q(\theta^k,\theta^k)$能否取等,那么取$Q$的最大值$Q(\theta^*,\theta^k)$时,尽管有$Q(\theta^*,\theta^k)\ge Q(\theta^k,\theta^k)$,但并不能保证$L(\theta^*)\ge L(\theta^k)$,迭代的不减性质就就没了。
我这里暂且把它看做一种巧合,是研究EM算法的大佬,碰巧想用Jenson不等式来迭代而构造出来的一种做法。本人段位还太弱,无法正向理解其中的缘故,只能以这种方式来揣度大佬的思路了。知乎大佬发的EM算法九层理解(点击链接),我当前只能到第3层,有时间一定要拜读一下深度学习之父的著作。
高斯混合模型的应用
迭代式推导
假设高斯混合模型混合了$m$个高斯分布,参数为$\theta = (\alpha_1,\theta_1,\alpha_2,\theta_2,...,\alpha_m,\theta_m),\theta_i=(\mu_i,\sigma_i)$则整个概率分布为:
$\displaystyle P(y|\theta) = \sum\limits_{i=1}^m\alpha_i \phi(y|\theta_i) = \sum\limits_{i=1}^m\frac{\alpha_i }{\sqrt{2\pi}\sigma_i}\exp\left(-\frac{(y-\mu_i)^2}{2\sigma_i^2}\right),\;\text{where}\;\sum\limits_{j=1}^m\alpha_j = 1$
对混合分布抽样$n$次得到$\{y_1,...,y_n\}$,则在第$k+1$次迭代,待优化式为:
$\begin{gather}\begin{aligned} &\max\limits_{\theta}Q(\theta,\theta^k) \\ =&\max\limits_{\theta}\sum\limits_{Y\in \mathcal{Y}}\sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta^k)\log P(Y,Z|\theta) \\ =&\max\limits_{\theta}\sum\limits_{Y\in \mathcal{Y}}\sum\limits_{Z\in \mathcal{Z}} \frac{P(Z,Y|\theta^k)}{P(Y|\theta^k)}\log P(Y,Z|\theta) \\ =&\max\limits_{\theta}\sum\limits_{i=1}^n\sum\limits_{j=1}^m \frac{\alpha_j^k\phi(y_i|\theta_j^k)} {\sum\limits_{l=1}^m \alpha_l^k\phi(y_i|\theta_l^k)} \log \left[\alpha_j\phi(y_i|\theta_j)\right] \\ =&\max\limits_{\theta}\sum\limits_{i=1}^n\sum\limits_{j=1}^m \frac{\alpha_j^k\phi(y_i|\theta_j^k)} {\sum\limits_{l=1}^m \alpha_l^k\phi(y_i|\theta_l^k)} \log \left[ \frac{\alpha_j}{\sqrt{2\pi}\sigma_j}\exp\left(-\frac{(y_i-\mu_j)^2}{2\sigma_j^2}\right) \right]\\ =&\max\limits_{\theta}\sum\limits_{j=1}^m \sum\limits_{i=1}^n \frac{\alpha_j^k\phi(y_i|\theta_j^k)} {\sum\limits_{l=1}^m \alpha_l^k\phi(y_i|\theta_l^k)} \left[ \log \alpha_j - \log \sigma_j-\frac{(y_i-\mu_j)^2}{2\sigma_j^2} \right]\\ \end{aligned} \label{}\end{gather}$
计算α
定义
$\displaystyle n_j = \sum\limits_{i=1}^n \frac{\alpha_j^k\phi(y_i|\theta_j^k)} {\sum\limits_{l=1}^m \alpha_l^k\phi(y_i|\theta_l^k)}$
则对于$\alpha$,优化式为
$\begin{gather} \begin{aligned} \max\limits_{\alpha}\sum\limits_{j=1}^m n_j \log \alpha_j \end{aligned} \label{}\end{gather}$
又因为$\sum\limits_{j=1}^m \alpha_j=1$,所以只需优化$m-1$个参数,上式变为:
$ \max\limits_\alpha \left[ \begin{matrix} n_1&n_2&\cdots &n_{m-1}&n_{m}\\ \end{matrix} \right] \cdot \left[ \begin{matrix} \log\alpha_1\\ \log\alpha_2\\ \vdots\\ \log\alpha_{m-1}\\ \log(1-\alpha_1-\cdots-\alpha_{m-1})\\ \end{matrix} \right] $
对每个$\alpha_j$求导并等于0,得到线性方程组:
$\left[\begin{matrix}n_1+n_m&n_1&n_1&\cdots&n_1\\n_2&n_2+n_m&n_2&\cdots&n_2\\n_3&n_3&n_3+n_m&\cdots&n_3\\&&&\vdots&\\n_{m-1}&n_{m-1}&n_{m-1}&\cdots&n_{m-1}+n_m\\\end{matrix}\right]\cdot\left[\begin{matrix}\alpha_1\\\alpha_2\\\alpha_3\\\vdots\\\alpha_{m-1}\\\end{matrix}\right]=\left[\begin{matrix}n_1\\n_2\\n_3\\\vdots\\n_{m-1}\\\end{matrix}\right]$
求解这个爪形线性方程组,得到
$\left[\begin{matrix}\sum_{j=1}^mn_j/n_1&0&0&\cdots&0\\-n_2/n_1&1&0&\cdots&0\\-n_3/n_1&0&1&\cdots&0\\&&&\vdots&\\-n_{m-1}/n_1&0&0&\cdots&1\\\end{matrix}\right]\cdot\left[\begin{matrix}\alpha_1\\\alpha_2\\\alpha_3\\\vdots\\\alpha_{m-1}\\\end{matrix}\right]=\left[\begin{matrix}1\\0\\0\\\vdots\\0\\\end{matrix}\right]$
因为
$\displaystyle \sum\limits_{j=1}^m n_j = \sum\limits_{j=1}^m\sum\limits_{i=1}^n \frac{\alpha_j^k\phi(y_i|\theta_j^k)} {\sum\limits_{l=1}^m \alpha_l^k\phi(y_i|\theta_l^k)}=\sum\limits_{i=1}^n \sum\limits_{j=1}^m \frac{\alpha_j^k\phi(y_i|\theta_j^k)} {\sum\limits_{l=1}^m \alpha_l^k\phi(y_i|\theta_l^k)} =\sum\limits_{i=1}^n 1 = n$
解得
$\displaystyle\alpha_j = \frac{n_j}{n} = \frac{1}{n}\sum\limits_{i=1}^n \frac{\alpha_j^k\phi(y_i|\theta_j^k)} {\sum\limits_{l=1}^m \alpha_l^k\phi(y_i|\theta_l^k)}$
计算σ与μ
与$\alpha$不同,它的方程组是所有$\alpha_j$之间联立的;而$\sigma,\mu$的方程组则是$\sigma_j$与$\mu_j$之间联立的。定义
$\displaystyle p_{ji} = \frac{\alpha_j^k\phi(y_i|\theta_j^k)} {\sum\limits_{l=1}^m \alpha_l^k\phi(y_i|\theta_l^k)}$
则对于$\sigma_j,\mu_j$,优化式为(比较$(6),(7)$式的区别)
$\begin{gather}\displaystyle\min\limits_{\sigma_j,\mu_j}\sum\limits_{i=1}^n p_{ji} \left(\log \sigma_j+\frac{(y_i-\mu_j)^2}{2\sigma_j^2} \right)\label{}\end{gather}$
对上式求导等于0,解得
$ \begin{aligned} &\mu_j = \frac{\sum\limits_{i=1}^np_{ji}y_i}{\sum\limits_{i=1}^np_{ji}} = \frac{\sum\limits_{i=1}^np_{ji}y_i}{n_j} = \frac{\sum\limits_{i=1}^np_{ji}y_i}{n\alpha_j}\\ &\sigma^2_j = \frac{\sum\limits_{i=1}^np_{ji}(y_i-\mu_j)^2}{\sum\limits_{i=1}^np_{ji}} = \frac{\sum\limits_{i=1}^np_{ji}(y_i-\mu_j)^2}{n_j} = \frac{\sum\limits_{i=1}^np_{ji}(y_i-\mu_j)^2}{n\alpha_j} \end{aligned} $
代码实现
对于概率密度为$P(x) = −2x+2,x\in (0,1)$的随机变量,以下代码实现GMM对这一概率密度的的拟合。共10000个抽样,GMM混合了100个高斯分布。
#%%定义参数、函数、抽样
import numpy as np
import matplotlib.pyplot as plt
dis_num = 100 #用于拟合的分布数量
sample_num = 10000 #用于拟合的分布数量
alphas = np.random.rand(dis_num)
alphas /= np.sum(alphas)
mus = np.random.rand(dis_num)
sigmas = np.random.rand(dis_num)**2#方差,不是标准差
samples = 1-(1-np.random.rand(sample_num))**0.5 #样本
C_pi = (2*np.pi)**0.5
dis_val = np.zeros([sample_num,dis_num]) #每个样本在每个分布成员上都有值,形成一个sample_num*dis_num的矩阵
pij = np.zeros([sample_num,dis_num]) #pij矩阵
def calc_dis_val(sample,alpha,mu,sigma,c_pi):
return alpha*np.exp(-(sample[:,np.newaxis]-mu)**2/(2*sigma))/(c_pi*sigma**0.5)
def calc_pij(dis_v):
return dis_v / dis_v.sum(axis = 1)[:,np.newaxis]
#%%优化
for i in range(1000):
print(i)
dis_val = calc_dis_val(samples,alphas,mus,sigmas,C_pi)
pij = calc_pij(dis_val)
nj = pij.sum(axis = 0)
alphas_before = alphas
alphas = nj / sample_num
mus = (pij*samples[:,np.newaxis]).sum(axis=0)/nj
sigmas = (pij*(samples[:,np.newaxis] - mus)**2 ).sum(axis=0)/nj
a = np.linalg.norm(alphas_before - alphas)
print(a)
if a< 0.001:
break
#%%绘图
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
def get_dis_val(x,alpha,sigma,mu,c_pi):
y = np.zeros([len(x)])
for a,s,m in zip(alpha,sigma,mu):
y += a*np.exp(-(x-m)**2/(2*s))/(c_pi*s**0.5)
return y
def paint(alpha,sigma,mu,c_pi,samples):
x = np.linspace(-1,2,500)
y = get_dis_val(x,alpha,sigma,mu,c_pi)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(samples,density = True,label = '抽样分布')
ax.plot(x,y,label = "拟合的概率密度")
ax.legend(loc = 'best')
plt.show()
paint(alphas,sigmas,mus,C_pi,samples)以下是拟合结果图,有点像是核函数估计,但是完全不同:
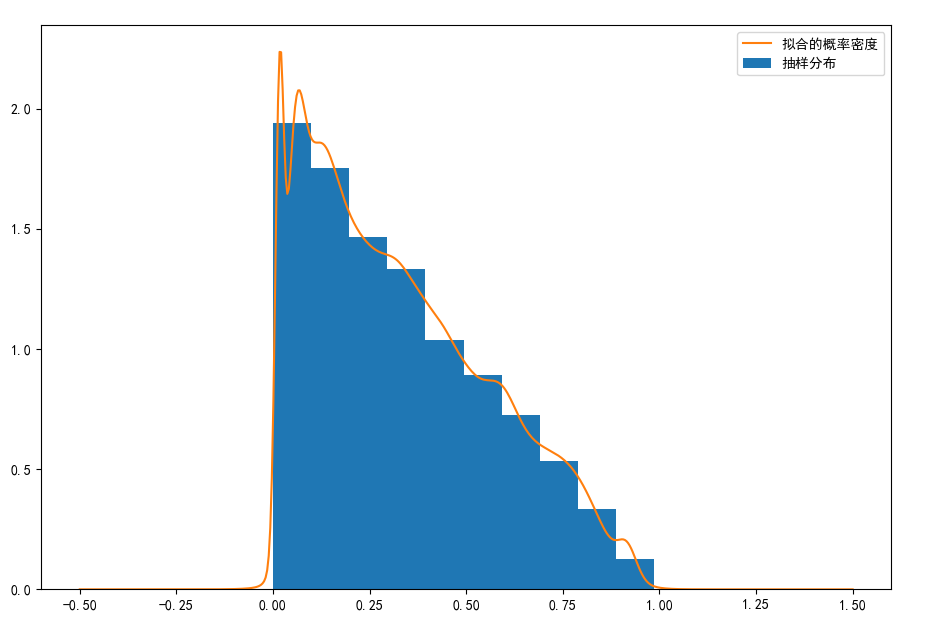
EM算法的推广
EM算法的推广是对EM算法的另一种解释,最终的结论是一样的,它可以使我们对EM算法的理解更加深入。它也解释了我在$(1)$式下方提出的疑问:为什么取出$P(Z|Y,\theta^k)$而不是别的。
定义$F$函数,即所谓Free energy自由能(自由能具体是啥先不研究了):
$ \begin{aligned} F(\tilde{P},\theta) &= E_{\tilde{P}}(\log P(Y,Z|\theta)) + H(\tilde{P})\\ &= \sum\limits_{Z\in \mathcal{Z}} \tilde{P}(Z)\log P(Y,Z|\theta) - \sum\limits_{Z\in \mathcal{Z}} \tilde{P}(Z)\log \tilde{P}(Z)\\ \end{aligned} $
其中$\tilde{P}$是$Z$的某个概率分布(不一定是单独的分布,可能是在某个条件下的分布),$E_{\tilde{P}}$表示分布$\tilde{P}$下的期望,$H$表示信息熵。
我们计算一下,对于固定的$\theta$,什么样的$\tilde{P}$会使$F(\tilde{P},\theta) $最大。也就是找到一个函数$\tilde{P}_{\theta}$,使$F$极大,写成优化的形式就是(这里是找函数而不是找参数哦,理解上可能要用到泛函分析的内容):
$ \begin{aligned} &\max\limits_{\tilde{P}} \sum\limits_{Z\in \mathcal{Z}} \tilde{P}(Z)\log P(Y,Z|\theta) - \sum\limits_{Z\in \mathcal{Z}} \tilde{P}(Z)\log \tilde{P}(Z)\\ &\;\text{s.t.}\; \sum\limits_{Z\in \mathcal{Z}}\tilde{P}(Z) = 1 \end{aligned} $
拉格朗日函数(拉格朗日对偶性,点击链接)为:
$ \begin{aligned} L = \sum\limits_{Z\in \mathcal{Z}} \tilde{P}(Z)\log P(Y,Z|\theta) - \sum\limits_{Z\in \mathcal{Z}} \tilde{P}(Z)\log \tilde{P}(Z)+ \lambda\left(1-\sum\limits_{Z\in \mathcal{Z}}\tilde{P}(Z)\right) \end{aligned} $
因为每个$\tilde{P}(Z)$之间都是求和,没有其它其它诸如乘积的操作,所以可以直接令$L$对某个$\tilde{P}(Z)$求导等于$0$来计算极值:
$ \begin{aligned} \frac{\partial L}{\partial \tilde{P}(Z)} = \log P(Y,Z|\theta) - \log \tilde{P}(Z) -1 -\lambda = 0 \end{aligned} $
于是可以推出:
$ \begin{aligned} P(Y,Z|\theta) = e^{1+\lambda}\tilde{P}(Z) \end{aligned} $
又由约束$\sum\limits_{Z\in \mathcal{Z}}\tilde{P}(Z) = 1$:
$P(Y|\theta) = e^{1+\lambda}$
于是得到
$\begin{gather}\tilde{P}_{\theta}(Z) = P(Z|Y,\theta)\label{}\end{gather}$
代回$F(\tilde{P},\theta)$,得到
$ \begin{aligned} F(\tilde{P}_\theta,\theta) &= \sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta)\log P(Y,Z|\theta) - \sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta)\log P(Z|Y,\theta)\\ &= \sum\limits_{Z\in \mathcal{Z}} P(Z|Y,\theta)\log \frac{P(Y,Z|\theta)}{P(Z|Y,\theta)}\\ &= \log P(Y|\theta)\\ \end{aligned} $
也就是说,对$F$关于$\tilde{P}$进行最大化后,$F$就是待求分布的对数似然;然后再关于$\theta$最大化,也就算得了最终要估计的参数$\hat{\theta}$。所以,EM算法也可以解释为$F$的极大-极大算法。优化结果$(8)$式也解释了我之前在$(1)$式下方的提问。
那么,怎么使用$F$函数进行估计呢?还是要用迭代来算,迭代方式是和前面介绍的一样的(懒得记录了,统计学习方法上直接看吧)。实际上,$F$函数的方法只是提供了EM算法的另一种解释,具体方法上并没有提升之处。
来源:oschina
链接:https://my.oschina.net/u/4258325/blog/4319088