- 练习题
- P5017 摆渡车
- P4910 【帕秋莉的手环】
- P4933 大师
- P1439 【模板】最长公共子序列
- P5858 「SWTR-03」Golden Sword
- P5664 Emiya 家今天的饭
- P1973 [NOI2011]NOI 嘉年华
- P1270 “访问”美术馆
- P2577 [ZJOI2005]午餐
- P2501 [HAOI2006]数字序列
- P4158 [SCOI2009]粉刷匠
- P1295 [TJOI2011]书架
- P1052 过河
- P2051 [AHOI2009]中国象棋
- CF79D Password
- P1040 加分二叉树
- P1273 有线电视网
- P3287 [SCOI2014]方伯伯的玉米田
- 学到了什么
去世选手请求重生。
练习题
P5017 摆渡车
算法一
设 \(f_i\) 在 \(i\) 时间发车,发车时等待的时间和的最小值。则显然有:
对于每个 \(f_i\),当在 \(i\) 时刻时发第一班车,\(f_i\)最大,则其初始值为:
为保证载上所有人,最后一班车需在 \([t_{max}, t_{max}+m)\)内发车,则:
前缀和优化,设 :
对于上式中的 \(\sum\limits_{j < t_k \le i}{i-t_k}\),有:
替换状态转移方程。
优化转移方程,对于状态转移方程:
显然,若 \(j\le i-2m\),则在 \(j+m\) 时刻可多发一班车,不影响在 \(i\) 时刻发车,且答案不会变劣。
即:停车时间 \(i- (j+m) < m\)。
故转移方程可替换为:
减去无用状态。
若 \(cnt_i=cnt_{i-m}\),说明时间段 \([i-m,i]\)内没有需要坐车的人。
则在 \(i-m\) 时刻发车,在 \(i\) 时刻不发车,不会使答案变劣,\(f_i\) 是一个无用状态。
则可将状态转移方程改为:
当满足 \(t_i = t_{i-1}+m\) 时,有用的位置最多,为 \(nm\) 个。
复杂度 \(O(nm^2 + t)\),期望得分 \(100\text{pts}\)。
算法二
由算法一,停车时间 \(i- (j+m) < m\)。
车往返一次时间 \(m\),则人等车时间 \(< 2m\)。
设 \(f_{i,j}\) 表示第 \(i\) 个人,等待时间为 \(j\),且前 \(i\) 个人已到达的时间最小值。
初始值 \(f_{1,i} = i\)。
分类讨论:
- 若 \(t_{i+1} \le t_{i+1} + j\),则第 \(i+1\) 个人可和 第 \(i\) 个人坐同一辆车走。
第 \(i+1\) 个人的等待时间 \(k = t_i+j-t_{i+1}\)
状态转移方程式为:
- 否则,枚举第 \(i+1\) 个人的等待时间 \(k\)。
\[k\in [\max(0, t_i + j + m - t_{i+1}), 2m) \]状态转移方程式同上,为:\[f_{i+1,k} = \min (f_{i+1}, k, f_{i,j} + k) \]
复杂度 \(O(nm^2)\),期望得分 \(100\text{pts}\)。
P4910 【帕秋莉的手环】
题目要求:
给定一个长度为 \(n\) 的环,填入 金色或绿色。
不能有两个相邻的绿色。
多组数据, \(T\le 10, n\le 10^{18}\)
矩阵加速模板。
设 \(f_{i,0/1}\) 为当前填到第 \(i\) 位,第一个位置为 金色/绿色 的合法方案数。
分成第一个位置为 绿/金讨论:
- 第一个位置为绿色时,\(f_{1,0} = 0,f_{1,1} = 1\)。
由于不能有两个相邻的绿色,则结尾珠子必为金色。
其对答案的贡献为 \(f_{n,0}\) - 第一个位置为金色时,\(f_{1,0} = 1, f_{1,1} = 0\)。
此时结尾珠子颜色任意。
其对答案的贡献为 \(f_{n,0} + f_{n,1}\)
状态转移方程:
\(f_{i,0} = f_{i-1,0} + f_{i-1,1}\)
\(f_{i,1} = f_{i-1,0}\)
复杂度 \(O(Tn)\),期望得分 \(\text{60pts}\)。
上式显然可矩阵加速,转移矩阵如下:
复杂度 \(O(T\log n)\),期望得分 \(\text{100pts}\)。
代码 P4910 【帕秋莉的手环】 - Luckyblock
P4933 大师
题目要求:
给定一长度为 \(n\) 的序列 \(h\)。
求方向为从左到右的,等差数列个数。
\(n\le 10^3, h_{max} \le 2 \times 10^4\)
显然的线性DP。
设 \(f_{i,j}\) 表示 最后一项是\(h_i\),公差为 \(j\) 的等差数列的个数。
转移到 \(i\) 时,枚举前一个元素 \(k\),公差 \(j\) 即为 \(h_i - h_k\)。
最后一项是 \(h_k\),公差为 \(j\) 的等差数列的个数为 \(f_{k,j}\)。

如图,在其末尾添加一新元素,则显然有 \(f_{i,j} = f_{k,j} +1\)。
可能存在多个公差为 \(j\) 的位置 \(k\),则有状态转移方程式:
需要枚举当前位置 和 前一个位置。
复杂度 \(O(n^2)\),稳过。
公差为负数怎么办?
- 为所有计算出的公差加上一个偏移量。
- 正着反着做两次DP,并将两次的贡献求和。
一种空间换时间,一种时间换空间。
代码中使用了时间换空间的做法。
P1439 【模板】最长公共子序列
题目要求:
给定 \(1,2,\dots n\) 的两个排列 \(a,b\),求其最长公共子序列。
\(n\le 10^5\)
算法一
有一个极其显然的做法。
设 \(f_{i,j}\) 为,\(a\) 中匹配到第\(i\) 位,\(b\) 中匹配到第 \(j\) 位时,最长公共子序列的长度。
讨论 \(a_i\) 与 \(b_j\) 是否相等,则有:
\(f_{i,j} = \begin{cases}f_{i-1,j-1} +1 & a_i=b_j\\\max ({f_{i,j-1}, f_{i-1,j}}) & \text{otherwise}\end{cases}\)
复杂度 \(O(n^2)\),期望得分 \(50\text{pts}\)。
算法二
上述算法已无法再优化,考虑奇技淫巧。
排列中不存在重复元素,考虑建立一一映射关系。
令 \(pos_{a_i} = i\),使 \(a_i \Rightarrow i, b_i \Rightarrow pos_{b_i}\)。
即发生如下的转化:
显然映射后的 LCS 的长度不会受影响。
由于 \(a_i\) 单调递增,则 LCS 也单调递增。
换言之,\(b\) 中所有单调递增子序列,均是一公共子序列。
问题转化为,求 \(b\) 最长的单调递增子序列的长度。
即经典的 LIS 问题。
使用 \(O(n\log n)\) 算法求解即可,期望得分 \(\text{100pts}\)。
代码 P1439 【模板】最长公共子序列 - Luckyblock
P5858 「SWTR-03」Golden Sword
题目要求:
给定 \(n\) 个物品,编号为 \(a_1\sim a_n\)。
现需要将其按顺序放到容量为 \(w\) 的箱子里。
每放入一个物品前,可以从箱子中取出 \(s\) 个物品。
定义 第 \(i\) 个物品的价值为,将其放入箱子后,箱中物品数 \(\times a_i\),求最大价值和。
\(1\le s\le w\le n \le 5.5\times 10^3, 0\le \mid a\mid \le 10^9\)
发现一些奇妙性质。
- 已经放入箱子的物品本质相同,对之后放入物品的贡献都为 \(1\)。
- 欲使加入新物品后,箱子内物品数为 \(j\),可在物品数为 \(j-1\) 直接加入,或删去 \(\le s\) 个物品。
但两种方法对答案的贡献等价。
则有非常显然的做法。
设 \(f_{i,j}\) 表示,放到第 \(i\) 个物品,箱子里有 \(j\) 个元素的最大价值和。
转移时只与 \(i-1\) 有关,则 \(i\) 维可以滚动数组滚掉,保证空间复杂度。
需每次都将 \(f_{now}\) 初始化为负无穷。
注意循环边界的细节。
for (int i = 1; i <= n; ++ i, now ^= 1) {
memset(f[now], 128, sizeof(f[now]));
for (int j = 1; j <= min(i, w); ++ j) {
for (int k = j - 1; k <= min(i, min(j + s - 1, w)); ++ k) {
f[now][j] = max(f[now][j], f[now ^ 1][k] + (ll) j * a[i]);
}
}
}
时间复杂度上限 \(O(n^3)\),在 \(s=w=n\) 时复杂度最高。
在随机数据下能骗到 \(\text{85pts}\)。
被 \(\text{Subtask 4}\) 卡掉了咋办啊?
观察代码:
for (int j = 1; j <= min(i, w); ++ j)
for (int k = j - 1; k <= min(i, min(j + s - 1, w)); ++ k)
发现 \(k\) 的范围区间,随 \(j\) 的增加,单调右移,考虑单调队列优化。
优化掉一重循环,省去了枚举 \(k\) 的复杂度。
复杂度 \(O(n^2)\),期望得分 \(\text{100pts}\)
代码 P5858 「SWTR-03」Golden Sword - Luckyblock
P5664 Emiya 家今天的饭
赛场上硬刚64pts 2.5h,最后样例没过。
没时间写爆搜,交了一份自己也不知道在干什么的代码,获得了 8pts 的好成绩。
留下了极大的心理阴影。
消除恐惧的最好方法,就是直面恐惧。
加油,奥利给!
题目要求:
给定一 \(n\times m\) 的矩阵 \(a\)。
从矩阵中取出一个集合,满足下列要求:
- 非空。
- 每一行只能选择一个元素。
- 属于同一列的元素数 \(\le \left\lfloor\frac{n}{2}\right\rfloor\)。
一个集合的价值定义为所有元素的乘积。
求所有满足条件的 集合的权值 之和,答案对 \(998244353\) 取模。
\(1\le n\le 100, 1\le m \le 2000, 0\le a_{i,j} \le 998244353\)。
考虑容斥,容易想到,合法集合权值和 = 总权值和 - 不合法集合权值和。
对于总权值和:
每一行可以选择 1 个元素,或者不选。
选择 1 个元素时,其对乘积的贡献为 \(a_{i,j}\),不选时贡献为 1。
最后减去空集的情况(其贡献为 1),则总权值和为:
对于不合法集合权值和:
由条件 3 可知,不合法集合中,只存在一个不合法列,使集合中位于该列的元素数 \(> \left\lfloor\frac{k}{2}\right\rfloor\)。
考虑通过枚举固定这一列。
判断某一集合是否合法,只需已知 位于该列的元素数,和位于其他列的元素数,求差值即可。
令枚举固定的一列为 \(now\),则可设计状态:\(f_{i,j,k}\) 表示:前 \(i\) 行中,\(now\) 列中 选择了 \(j\) 个,其他列中选择了 \(k\) 个的权值和。
令 \(s_{i,now} = \sum\limits_{j=1}^{m}a_{i,j} - a_{i,now}\),表示一行中非 \(now\) 行的元素之和。
则有显然的转移方程:
复杂度 \(O(n^3m)\),期望得分 \(84\text{pts}\)。
考虑优化:
由上述算法,判断集合是否合法,仅需知道 被枚举列和 其他列元素数的差值。
分别记录两种元素的个数是没有必要的。
考虑直接记录差值。
算法四转移方程中 \(f_{i-1,j-1,k}\rightarrow f_{i-1,j,k}\) 和 \(f_{i-1,j,k-1}\rightarrow f_{i-1,j,k}\),可看做差值的 增大 / 减小。
同样令固定的一列为 \(now\),可设计新状态,令 \(f_{i,j}\) 表示,前 \(i\) 行中, \(now\) 列中 选择个数 与 其他列个数差值为 \(j\) 时的权值和。
令 \(s_{i,now} = \sum\limits_{j=1}^{m}a_{i,j} - a_{i,now}\),表示一行中非 \(now\) 行的元素之和。
则有状态转移方程:
复杂度 \(O(n^2m)\),期望得分 \(100\text{pts}\)。
代码 P5664 Emiya 家今天的饭 - Luckyblock
P1973 [NOI2011]NOI 嘉年华
参考: stO FlashHu 的题解 Orz
蒟蒻尽量把悟到的信息都放了上来。
比较啰嗦,望见谅。
题意简述:
给定 \(n\) 个事件,第 \(i\) 个事件从 \(S_i\)时刻开始,持续 \(T_i\) 时刻。
可将它们分到两个地点中的一个,或者放弃。
同一地点事件可同时发生,两个事件不可同时发生在不同地点。
求
- 无限制时,事件数较小的地点 的事件数。
- 不放弃第 \(i\) 个事件时,事件数较小的地点 的事件数。
\(1\le n \le 200, 0\le S_i\le10^9,1\le T_i\le 10^9\)。
先离散化,下文中出现的 “时间” 均指离散化后的值。
显然,离散化后时间的最大值 \(\le 2n\)。
把事件看做线段,地点看做集合。
从 \(S_i\)时刻开始,持续 \(T_i\) 时刻的事件记为 \([s_i,t_i]\)。
有一个很显然的结论:
对于一个分配方案,若存在某被丢弃的事件,可加入到集合中。
将其加入,答案不会变劣。
由上,若向某一集合中添加了一条线段 \([L,R]\),则所有包含于 \([L,R]\) 的线段,都一定会被添加到该集合中。
则可考虑将一个区间内的完整线段合并,
设 \(cnt_{i,j}\) 表示区间 \([i,j]\) 内的完整线段数。
暴力 \(O(n^3)\) 预处理即可。
先搞掉子任务一。
要求:事件数较小的地点 的事件数。
数据范围不大,考虑枚举一边的事件数,并求另一边的最大值,两边取 \(\min\) 即为所求。
设 \(pre_{i,j}\) 表示,枚举到时间 \(i\),一边线段数为 \(j\) 时,另一边线段数的最大值。
转移时枚举断点 \(k\),则有:
两种情况分别代表将 \([k,i]\) 添加到两边的情况。
转移的总复杂度为 \(O(n^3)\)。
令 \(m\) 为时间的最大值,显然答案为 \(\max\limits_{j=1}^{n}\{\min(pre_{m,j},j)\}\)。
来搞子任务二。
\(pre_{i,j}\),即为 \(1\sim i\) 中,一边线段数为 \(j\) 时,另一边线段数的最大值。
再处理一个 \(suf_{i,j}\),表示 \(i\sim m\) 中,一边线段数为 \(j\) 时,另一边线段数的最大值。
转移方程与 \(pre_{i,j}\) 类似,即为:
此时属于 \([s_i,t_i]\) 的线段,必包含在其中同一边,但\(s_i\) 之前和 \(t_i\) 之后选择的线段数 均未知。
同子任务一的思路,考虑枚举线段数,并求另一集合线段数的最大值,两边取 \(\min\) 即为所求。
设 \(f_{l,r}\) 为保证一边必选 \([l,r]\) 中线段时,最优的答案。
枚举 \(x\) 为这边中属于 \([1,l-1]\) 的线段数, \(y\) 为 \([r+1,m]\) 中的线段数。
这一边线段总数即为 \(x + cnt_{i,j} + y\)。
另一边选择的最大个数,显然为 \(pre_{l,x} + suf_{r,y}\)。
则有状态转移方程:
所以答案就是 \(f_{s_i,t_i}\) 吗?回答是否定的。
还有一种特殊情况:
当 \([s_i,t_i]\) 被一属于同一集合的某线段包含,即存在包含询问区间的线段时,上述 \(pre_{l,x} + suf_{r,y}\) 的计算方法就不合适了。
考虑枚举这样的线段,以包含所有特殊情况。
显然,第 \(i\) 个事件必选的答案即为:\(\max\limits_{l=1}^{s_i}\max\limits_{l=t_i}^{m}f_{l,r}\)。
这样就必须预处理出所有 \(f_{i,j}\),其复杂度达到 \(O(n^4)\),会被卡掉。
考虑一波优化。
显然, \(pre_{l,x}\) 随 \(x\) 的增加而减小,\(suf_{r,y}\) 随 \(y\) 的增加而减小。
当一边选的多了,另一边选择的余地自然少。
观察上面的式子,答案即最大的 \(\min(x + cnt_{l,r} + y,\ pre_{l,x} + suf_{r,y})\),考虑如何最大化它的值。
当 \(x\) 固定时,\(x + cnt_{l,r}\) 与 \(pre_{l,x}\) 均不变。
正序枚举 \(y\),\(suf_{r,x}\) 递减。此时 有\((x + cnt_{l,r} + y)\uparrow\) 而 \((pre_{l,x} + suf_{r,y})\downarrow\)。
讨论一波,显然有下图形式:
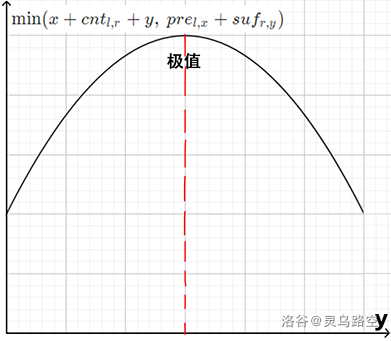
它是一关于 \(y\) 的单峰函数。在峰值左侧有 \(x + cnt_{l,r} + y< pre_{l,x} + suf_{r,y}\),函数递增。右侧则相反。
当 \(x\) 增加时,\(x + cnt_{l,r}\) 增加,\(pre_{l,x}\) 减小。单峰函数的极值会在 \(y\) 更小时取到,有:
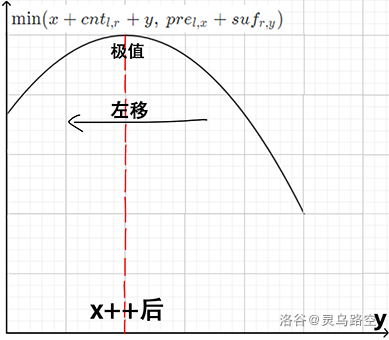
发现 在 \(x\) 增加时,令答案更优的 \(y\) 单调递减。
则可在正序枚举 \(x\) 的同时,设立一指针指向 最优的 \(y\),单调左移即可。
省去一层循环,复杂度 \(O(n^3)\),期望得分 \(100\text{pts}\)。
调了很久发现是离散化挂掉了
代码 P1973 [NOI2011]NOI 嘉年华 - Luckyblock
P1270 “访问”美术馆
先扒茬扒茬性质:
- 到达一个房间的路径只有一条,显然屋子呈一树形结构,且只有到达叶节点才有贡献。
- 没有给出具体房间个数,但总时间 \(T \le 600s\),可知节点数较少。
- 在警察赶来之前 逃走,则花费时间 \(< T\)
先 dfs 建树,考虑树形 DP。
令 \(f_{u,i}\) 表示,在根节点为 \(u\) 的子树中,取得 \(i\) 幅画并回到 节点 \(u\) 的最小时间花费。
变成了一个树形背包问题。
暴力求解即可,边界为 \(f_{u,0} = 0\),有:
对于叶节点,有:
注意转移时不可直接更新 \(f_{u,i}\),会造成以新换新。
倒序枚举 \(i\),使 \(f_{root,i}<T\) 的第一个 \(i\) 即为答案。
由于是二叉树,复杂度为 \(O(n^3)\) 级别,期望得分 \(100\text{pts}\)。
发现是优美的二叉树,做树形背包小题大做了。
可直接枚举 左右儿子中选择的数量来更新答案。
有:
复杂度 \(O(n^3)\) 级别,期望得分 \(100\text{pts}\)。
P2577 [ZJOI2005]午餐
设第 \(i\) 个人打饭时间,吃饭时间分别为 \(a_i\) 与 \(b_i\),前 \(i\) 个人打饭时间总和为 \(sum_i\)。
先考虑只排一队的情况,对于一给定的队列完成的时间,有:
答案即为 最小的完成时间。
对于两个相邻的人, \(i\) 与 \(i+1\),若 \(b_{i+1} > b_i\)
- 当 \(i+1\) 在后面时,两者完成时间分别为 \(sum_i + b_i, sum_i+a_{i+1}+b_{i+1}\)。
显然有 \(sum_i+a_{i+1}+b_{i+1}> sum_i + b_i\)。 - 当 \(i+1\) 在前面时,完成时间分别为 \(sum_i+b_{i+1}, sum_{i} + a_i+b_i\)。
显然有 \(sum_i+a_{i+1}+b_{i+1} > \max\{sum_i+b_{i+1}, sum_{i} + a_i+b_i\}\)。
欲使 \(\max\limits_{i=1}^{n}\{sum_i+b_i\}\) 尽可能小,显然使 \(i+1\) 排在前面更优。
感性理解,吃饭慢的放在前面一定更优。
则可先将 \(n\) 个人按照吃饭时间降序排序。
逐个加入队列的人变成有序的了。
考虑线性 DP 求解此题。
发现有两边,不好设状态。
考虑 P1973 的思路,枚举一边的答案,并求另一边答案的最小值,两边取 \(max\) 即为所求。
设 \(f_{i,j,k}\) 表示 \(1\sim i\) 中,窗口一最后一个人为 \(j\),完成时间为 \(k\) 时,窗口二的完成时间。
然后发现无法转移,因为最后一个人不一定 最晚吃完。
陷入思考...

手搓的心心.png
发现窗口二的队列,必定为窗口一的补集。
设当前第 \(i\) 个人加入队列,令窗口一队列打饭时间总和为 \(j\),则窗口二打饭时间总和为 \(sum_i - j\)。
若已知 \(j\),可计算第 \(i\) 个人加入窗口一/二的完成时间。
考虑枚举窗口一打饭时间总和 \(j\),来更新答案。
设 \(f_{i,j}\) 表示,前 \(i\) 个人加入队列,窗口一队列打饭时间总和为 \(j\)时,两窗口的最小完成时间。
考虑第 \(i\) 个人排到窗口一/二:
- 排到窗口一,\(f_{i,j} = \max\{j + b_i,\ f_{i-1,j-a_i}\}\)。
\(j + b_i\) 为新加入窗口一的人的完成时间。
\(f_{i-1,j-a_i}\) 为:不加此人时,窗口一的完成时间 与 窗口二的完成时间 的最小值,用于更新答案,不会导致漏解。 - 排到窗口二,\(f_{i,j} = \max\{f_{i-1,j},\ sum_i-j+b_i\}\)。
\(sum_i-j+b_i\) 为新加入窗口二的人的完成时间。
\(f_{i-1,j}\) 也为不加此人时,窗口一的完成时间 与 窗口二的完成时间 的最小值。
上述两种情况取最小值即可。
复杂度 \(O(nT)\) (\(T\) 为最大时间),期望得分 \(100\text{pts}\)。
代码 P2577 [ZJOI2005]午餐 - Luckyblock
P2501 [HAOI2006]数字序列
太妙了,学到虚脱.
题意简述
给定一长度为 \(n\) 的数列 \(a\),可将 \(a_i\) 改为任意整数 \(k\),代价为 \(\mid a_i -k\mid\)。
求使数列变为单调严格上升序列,最少需要改变的个数。
及改变数最少时,最小的代价和。
\(1\le n\le 3.5\times 10^4, 1\le a_i\le 10^5\)。
先搞掉第一问。
需要改变最少,则需保留得尽可能多。
考虑保留两个数的条件,对于 \(a_i,a_j(i < j)\),若可保留,说明 \(a_i < a_j\) 且改变 \([i+1,j-1]\) 内的数,可使序列 \([i,j]\) 严格上升。
如数列 \(1, 4, 5, 3\) (无歧义),虽然满足 \(1<3\),但它们中间的两个数无论改成多少,都无法满足单增性质。
显然保留 \(a_i,a_j\) 的条件为:\(a_j-a_i \ge j-i\)。
移项,得 \(a_j - j \ge a_i - i\)。
发现保留 \(a_i\) 的条件为 \(a_i-i\) 单调不降。
设 \(b_i = a_i - i\)。
使用经典 \(O(n\log n)\) 的方法,求数列 \(b\) 的最长不下降子序列长度,即为答案。
来搞第二问。
发现使 \(a_i\) 单调上升的代价,等价于使 \(b_i\) 单调不降的代价。
有个结论:
对于区间 \([l,r]\),使其单调不降,则存在分界点 \(k\),使 \(b_i = b_l(i\le k), b_j = b_r (j>k)\),此时代价最小。
如何证明这个听起来很扯皮的结论?
考虑做第一问时,顺便维护一下每个数的从哪里转移而来。
设转移前驱为 \(pre_i\)。
显然,\(pre_i\) 为满足 \(b_i \ge b_{pre_i}\) 的,且使子序列最长的位置。
则不存在 \(pre_i<j<i\),使 \(b_j\le b_i\),否则 \(pre_i = j\) 显然更优。
考虑 \(pre_i\) 和 \(b_i\) 之间的数 \(b_j\),一定满足 \(b_j < b_{pre_i}\) 或 \(b_j>b_i\),它们一定要被修改。
设 \(b_j\) 修改后为 \(c_j\),显然 \(c_j\) 单调不降,且 \(b_{pre_i} \le c_j\le b_i\)。
则有下图形式: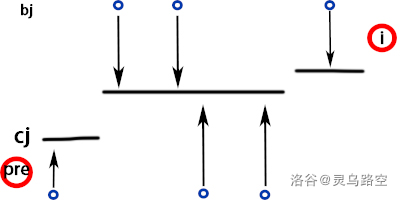
上图给出了一种修改的方案,考虑能否调整方案,使答案更优。
分类讨论:
对于一段被改为 \(c\) 的连续区间 \([l,r]\):
- 若 \(b_j < b_{pre_i}\) 的数量大于 \(b_j > b_{pre_i}\) 的数量,则 \(c\) 越小,代价越小。
又要保证单调不降,则 \(c = c_{l-1}\) 时最优。 - 若 数量相反,分析过程同上,\(c = c_{r+1}\) 时最优。
- 若 数量相等,\(c\) 可取任意值。
则可对此方案进行调整: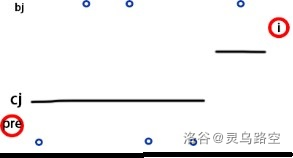
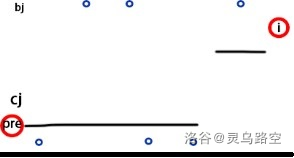
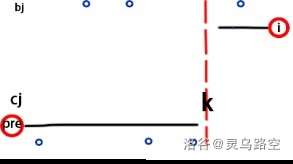
发现满足结论形式。
则对于任意不满足结论的方案,均可进行调整,使代价更小,最终必定调整至结论中的形式。
令 \(g_i\) 表示,最后一位是 \(b_i\) 时单调不降的代价。
枚举满足条件的前驱 \(pre\),转移 \(b_i\),
枚举的前缀满足:
- \(pre_i < i, b_{pre}\le b_i\)。
- 以\(b_{pre}\)结尾的 最长不降子序列长度 = 以 \(b_i\) 结尾的 - 1。
之后枚举分界 \(k\),求得最小的代价。
有:
后面那一大堆 \(\sum\) 可以用前缀后缀和优化。
复杂度 \(O(n^2)\) 级别?但数据随机,\([pre_i,i]\) 的长度较小,可以跑过去。
代码中用 vector 记录长度为 \(i\) 的最长不降子序列的结尾,再通过判断确定转移前缀。
\(from\) 表示转移前缀,\(pre\) 表示前缀和。
注意不开 long long 爆零两行泪。
代码 P2501 [HAOI2006]数字序列 - Luckyblock
P4158 [SCOI2009]粉刷匠
?这波算是大暴力草了过去
题意简述
给定一 \(N\times M\) 的空白矩阵,以及每个格子的目标颜色(为只能为红 / 蓝)。
每次可选择一行上连续的一段,涂上一种颜色。
每个格子最多只能被粉刷一次。
可涂色 \(T\) 次,求最多正确粉刷的个数。
\(1\le N,M\le 500,0\le T\le 2500\)。
注意 每个格子最多只能被粉刷一次。
由于这个性质,一个格子不会被多次更改颜色。
无后效性,可考虑线性 DP。
一开始没注意到,往区间 DP 往上莽了一阵
先考虑一行的情况:
把红色格子当作 0,蓝色看成 1。
显然一段连续同色区段,可以一次涂完。
考虑将连续同色区段合并,如下图形式:
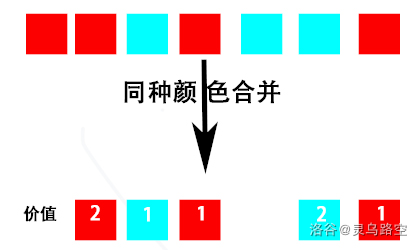
发现合并后的一行变成 0/1 交替的形式。
上一个格子与这一个目标状态一定不同。
以下提到格子,均指合并后的格子。
考虑新加入一个格子 \(i\),对花费的影响。
由上,影响新格子的,只有最后一个格子的状态。
- 当上一个格子刷错时,可顺便刷对新格子,花费不变。
- 当上一个格子刷对时,要想刷对新格子,必须多花费一次。
- 当上一个格子刷对时,刷错新格子,总花费不变。
- 当上一个格子刷错时,刷错新格子,必须多花费一次。
格子刷错对答案无贡献,刷对时对答案贡献为 \(val_i\)
设 \(f_{i,j,k, 0/1}\) 表示,第 \(i\) 行,在 \(1\sim j\) 中刷 \(k\) 次,第 \(j\) 个格子刷 错/对时,能刷对的最多格子数。
设 \(val_{i,j}\) 为格子 \((i,j)\) 的权值,显然有:
合并后每行格子长度变小,复杂度上限 \(O(nmT)\)。
显然,第 \(i\) 行刷 \(j\) 次后,能刷对的最多格子数为:
每行只能做一次贡献,涂色总次数为 \(T\),自此变成了一个分组背包问题。
数据范围较小,可暴力 \(O(nT^2)\) 实现。
直接暴力显然显然过不去,加个小剪枝,使每行涂色数 \(\le\) 格子数即可。
代码中数组 \(val\) 有两种含义,注意重新赋值时含义的变化。
代码 P4158 [SCOI2009]粉刷匠 - Luckyblock
P1295 [TJOI2011]书架
双倍经验 P1848 [USACO12OPEN]Bookshelf G。
这边有 dalao 的神仙题解。
?我一开始为什么要写二维 DP
题意简述
给出一个长度为 \(n\) 的序列 \(h\)。
将 \(h\) 分成若干段,满足每段数字之和都不超过 \(m\)。
最小化每段的最大值之和。
\(1\le n\le 10^5, 1\le h_i\le 10^9\)
有个非常显然的 DP :
设 \(f_i\) 表示,已经分好 \(i\) 个数字的最小代价。
转移时枚举这一段的开头 \(k\),将 \([k,i]\) 作为新的一段,则有:
暴力 DP 复杂度 \(O(n^2)\),期望得分 \(30\text{pts}\)。
实际上能水 \(50\text{pts}\)(大雾
考虑优化。
显然,对于一个给定的 \(i\),当 \(k\) 单增时,\(\max\limits_{j=k}^{i}h_j\) 单调不增,\(f_{k-1}\) 单调不降。
当枚举到 \(i\) 时,\(f_{k-1}\) 不会再改变,考虑 \(h_i\) 对 \(\max\limits_{j=k}^{i}h_j\) 的影响。
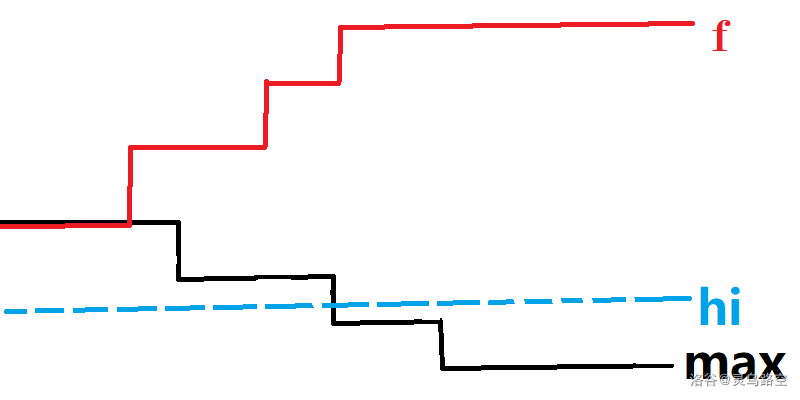
如图,设 \(i\) 左侧第一个满足 \(h > h_i\) 的位置为 \(pre_i\),显然 \(\max\limits_{j=k}^{i}h_j(k> pre_i)\) 都会变为 \(h_i\)。
\(\max\limits_{j=k}^{i}h_j\) 可用支持区间赋值的数据结构进行维护,转移 \(f_i\) 时,需要进行区间查询。
考虑线段树。
线段树维护位置 \(k\) 的 \(f_{k-1}\) 和 \(f_k+\max\limits_{j=k}^{i} h_j\)。
当枚举到一个新的 \(h_i\) 时:
- 单点修改,更新位置 \(k=i\) 时的 \(f_{k-1}\)。
- 根据 \(h_i\) 更新区间 \([pre_{i}+1,i]\) 的 \(f_k+\max\limits_{j=k+1}^{i} h_j\)。
- 二分得到 第一个不满足 \(\sum\limits_{k}^{i}h_i\le m\) 的位置 \(l\),则 \(k\in [l+1,i]\)。
- 查询 \([l+1,i]\) 中最小的 \(f_{k-1} + \max\limits_{j=k}^{i}h_j\)。
复杂度 \(O(n\log n)\),期望得分 \(100\text{pts}\)。
代码 P1295 [TJOI2011]书架 - Luckyblock
P1052 过河
题意简述
给定一数轴,标号 \(0\sim L\)。
从 \(0\) 出发,每次可向右移动 \(S\sim T\) 个单位。
数轴上有 \(M\) 个点,求移动到数轴外,经过的最少的点数。
\(1\le M\le 100,\ 1 \le L\le 10^9, 1\le S\le T\le 10\)。
算法一
我会暴力!
设 \(f_i\) 表示,到达 \(i\) 时,经过的最少的点数。
令 \(a_i\) 表示位置为 \(i\) 的点的数量,则有:
\(S,T\) 较小,可看做常数,复杂度 \(O(L)\) 级别。
期望得分 \(30\text{pts}\)。
算法二
发现 \(M \le 100\),但 \(L\le 10^9\)。
数轴上有大段的空白区域没有点存在,这些位置对答案无贡献。
而算法一中仍然在这些位置进行了转移,浪费了大量时间。
当 \(S < T\) 时:
发现有很多移动距离,都可以凑出来。
这个问题类似 Noip2017 D1T1 小凯的疑惑。
如 \(S=5, T=6\) 时,最大的凑不出来的距离为 \(19\),比 \(19\) 更大的距离均可凑出来。
考虑两个距离过大的点。
显然,从左边的点出发,最大的凑不出来的距离 右侧的位置(包括右侧的点),均可通过凑距离到达。
而两个点之间的位置 对答案无贡献。
在不影响 可到达性的同时,可考虑将两点距离缩小。
缩小到仍出现 上述任意点可到达的情况,不影响答案。
以下有两种缩法:
- \(2520\) 缩,由于 \(\operatorname{lcm}(1\sim 10) = 2520\),距离为 \(2520\) 时,必然出现上述情况。
- \(71\) 缩, \(9,10\) 凑不出来的最大距离为 \(9 \times 10 - 9 - 10 = 71\),则距离 \(71\) 是出现上述情况的最小值。
题解中神仙们给了缩距离的详细证明 Luogu题解。
复杂度 \(O(kM)\) (\(k\) 为缩成的距离),期望得分 \(100\text{pts}\)。
WA 成 80 了。
发现算法二并不适用于 \(S=T\) 的情况。
\(S=T\) 时,移动路径已知,先后经过 \(S,2S,...,kS\) 这些点。
则 位置为 \(S\) 的倍数的点的数量 即为答案。
P2051 [AHOI2009]中国象棋
题意简述
给定一张 \(N\times M\) 的棋盘。
求每一行,每一列棋子数 \(<3\) 的方案数。
\(1\le N,M \le 100\)。
合法的一行最多只有 \(2\) 个棋子,且只能放在棋子数 \(<2\) 的列上。
当枚举到第 \(i\) 行时,棋子数相等的两列是等价的,棋子的位置并没有影响。
考虑枚举 每种棋子数的列数,及这 \(2\) 个棋子的位置进行转移。
设 \(f_{i,j,k}\) 表示,前 \(i\) 行,有 \(j\) 列有 \(1\) 个棋子,\(k\) 列有两个棋子,合法的方案数。
显然有 \(m-j-k\) 列没有棋子。
考虑放棋子的个数:
- 不放时,贡献为 \(f_{i-1,j,k}\)。
- 放一个时:
- 放到没有棋子的一列,会使棋子为 \(1\) 的列数 + 1。
有 \(m-(j-1)-k\) 行没有棋子,则有这些种放置方案。
则贡献为 \(f_{i-1,j-1,k}\times (m-(j-1)-k)\)。 - 放到棋子数为 \(1\) 的一列,会使棋子为 \(1\) 的列数 - 1,会使棋子为 \(2\) 的列数 + 1。
有 \(j+1\) 种放置方案,则贡献为 \(f_{i-1,j+1,k-1}\times (j+1)\)。
- 放到没有棋子的一列,会使棋子为 \(1\) 的列数 + 1。
- 放两个时:
- 都放到没有棋子的列,贡献为 \(f_{i-1,j-2,k}\times C((m-(j-2)-k),2)\)。
- 都放在有 \(1\) 个棋子的列,贡献为 \(f_{i-1,j+2,k-2} \times C(j+2,2)\)。
- 一个放在有棋子的一列,一个放在有 \(1\) 个棋子的一列。
此时棋子数为 \(1\) 的列数不变。
贡献为 \(f_{i-1,j,k-1} \times j \times (m-(j-1)-k)\)。
贡献求和,即为 \(f_{i,j,k}\) 的值。
代码 P2051 [AHOI2009]中国象棋 - Luckyblock
CF79D Password
双倍经验 P3943 星空。
将此题代码交过去可直接 AC,但 P3943 数据较弱,没有卡掉错误的背包解法。
完全背包解法错误原因 详见 题解 P3943 【星空】 - Epworth 的博客。
给定一长度为 \(n\) 的 \(0\) 串,给定 \(k\) 个 位置。
给出 \(m\) 个长度 \(b_i\),每次可选择一段长度为 \(b_i\) 的子序列取反。
求使 \(k\) 个位置变为 \(1\) ,其他位置仍为 \(0\) 的最小步数。
\(1\le n\le 10^4,\ 1\le m\le 100,\ 1\le b_i\le n,\ k\le 10\)。
发现题目等价于 一开始只有 \(k\) 个位置开着灯,使所有灯都关上的最小步数。
设关灯为 \(0\),开灯为 \(1\),以下均按照上述等价情况展开。
看到区间修改,考虑差分。
但此题为区间取反,一般的作差差分无法使用,考虑异或差分。
令 \(b_i = a_i\ \text{xor}\ a_{i+1}\),对于样例 1,有:
| 差分前 | \(\ \ 1 1 1 0 1 1 1 1 1 0\) |
|---|---|
| 差分后 | \(10011000010\) |
在差分后数组前添加一个 \(0\) 位置。
手玩后发现,差分后必然有偶数个 \(1\) 出现。
此时若进行区间取反,只会使区间两端位置改变,中间不变。
若将原序列中 \(1\sim 3\) 取反,则有:
| 差分前 | \(\ \ 0 0 0 0 1 1 1 1 1 0\) |
|---|---|
| 差分后 | \(00001000010\) |
发现只有 \(0,3\) 两个位置的 \(1\) 被改变。
则问题转化为:
给定一有 \(2k\) 个位置为 \(1\) 的 01 串。
每次可选择一对距离为 \(b_i\) 的位置,将其取反。
求将其变为 \(0\) 串的最小步数。
分类讨论,进行下一步转化:
- 将一对 \(0\) 取反,显然会使答案更劣,不可能发生。
- 将一个 \(0\) 一个 \(1\) 取反,可看做原有的 \(1\) 移动至 \(0\) 的位置。
- 将一对 \(1\) 取反,可看做一个 \(1\) 移动到另一个的位置,两个 \(1\) 碰撞变成 \(0\)。
一定会发生偶数次 两个 \(1\) 碰撞的情况。
考虑每次使两个 \(1\) 碰撞的最小代价。
若已知两个 \(1\) 的位置为 \(u,v\),使其碰撞的代价即 使用 \(b_i\) 和 \(-b_i\) 凑出 \(v - u\) 的步数。
显然可以 bfs 预处理出碰撞每对 \(1\) 的花费。
问题转化为:
给定 \(2k\) 个物品,每次可取出一对物品。
取出每对物品的花费已知,求全取出的最小花费。
由于 \(k\le 10\),显然可以压缩 \(k\) 个物品选/不选的状态。
接下来就是个很简单的状压了。
每次枚举两个不在集合中的物品 加入集合转移即可。
代码 CF79D Password - Luckyblock
P1040 加分二叉树
一个 \(n\) 个节点的二叉树的中序遍历为 \(1,2,\dots n\)。,每个节点都有一个分数 \(w_i\)。
定义一颗子树的加分为:根的左子树的加分 \(\times\) 根的右子树的加分 \(+\) 根的分数,空子树的加分为 \(1\)。
求二叉树的最高加分,及此时的前序遍历。
\(n\le 30, w_i < 100\)。
有个中序遍历的性质:
中序遍历可看做 “拍扁序”,
其每一个子序列 都表示 树联通的一部分。
显然 每一个子序列都满足最优子结构性质。
可求出其最优组成结构,接到其他部分上。
考虑 DP。
设 \(f_{l,r}\) 表示子序列 \([l,r]\) 构成的树的最大加分。
对于空子树的情况,初始化 \(f_{i,i-1} = 1\)。
考虑枚举根 \(k\) 进行转移,则有:
可通过 区间 DP / 记忆化搜索实现。
由于要输出前序遍历,考虑维护 \(root_{l,r}\) 表示最大加分时 \([l,r]\) 的根。
在更新 \(f_{l,r}\) 时顺便维护,输出时递归输出即可。
P1273 有线电视网
题意简述
给定一棵根节点为 \(1\),节点数为 \(n\) 的树,边有边权。
有 \(m\) 个叶节点,叶节点有点权。
选择一棵以 \(1\) 为根的子树,使选择的边权值 \(\le\) 点权值。
最大化选择的叶节点的数量。
\(1\le m<n \le 3000\)。
显然可以树形 DP,考虑状态设计。
设状态记录 选择的叶节点的个数时,无法处理边权值 \(\le\) 点权值的限制。
移项有:点权值 \(-\) 边权值 \(\ge 0\),考虑记录 点权值 \(-\) 边权值的大小。
设 \(f_{i,j}\) 表示,以 \(i\) 为根的子树中选择了 \(j\) 个叶节点时,点权值 \(-\) 边权值最大值。
显然,答案为满足 \(f_{1,j} \ge 0\) 的 \(j\) 的最大值。
有转移方程:
表示从 \(v\) 的子树中取出 \(k\) 个子节点加入 \(u\) 的子树中,同时计算 \(u,v\) 边权的贡献。
\(size_v\) 为 子树 \(v\) 中叶节点的个数。
可将从 \(v\) 中取出 \(1,2,\dots k\) 个叶节点的贡献,看做 \(k\) 个体积分别为 \(1\sim k\) 的,不同的物品。
\(v\) 只能做一次贡献,是一个显然的分组背包问题。
为防止重复贡献,枚举 \(j\) 时应倒序枚举。
P3287 [SCOI2014]方伯伯的玉米田
题意简述
给定一长度为 \(n\) 的序列 \(a\),可进行最多 \(k\) 次区间 \(+1\) 操作。
求操作后的最长不下降子序列长度。
\(1<n<10000, 1< k\le 500, 1\le a_i \le 5000\)。
先猜个结论:所有修改操作的右端点一定为 \(n\)。
设修改区间为 \([l,r]\),显然修改区间内部 元素相对大小不变。
左侧元素不变,\([1,l-1]\) 的 不下降子序列 不变。
则区间增高后,\([1,r]\) 的 最长不下降子序列 长度 只会增不会减。
而 右侧元素不变,区间增高后,可能无法接到 \([l,r]\) 元素的后面,会导致 最长不下降子序列 减小。
为保证答案最优,则应使 \(r = n\)。
有了这个结论就可以暴力转移了。
设 \(f_{i,j}\) 表示,以位置 \(i\) 结尾,\(i\) 已经被 \(j\) 个区间覆盖时,\([1, n]\) 中最长不下降子序列长度,则有:
复杂度 \(O(n^2k^2)\),期望得分 \(0\text{pts}\)。
考虑优化。
观察状态转移方程,发现 \(f_{k,l}\) 是满足 \(1\le k<i,\ 0\le l\le j,\ a_k+l \le a_i+j\) 的一个三维前缀最大值。
\(i\) 维可以通过枚举消除,问题变为二维前缀最大值问题。
考虑二维树状数组优化。
修改状态,设 \(f_{j,k}\) 为 \(1\sim i-1\) 中,被不超过 \(j\) 个修改区间覆盖,结尾 \(\le k\) 的最长不下降子序列的长度。
直接用树状数组维护 \(f\) 即可。
注意 \(j\) 可以为 \(0\),树状数组的 \(j\) 维整体右移一位, \(j+1\) 实际上表示使用了 \(j\) 次修改。
由于通过枚举消除了 \(i\),为防止重复更新,套用01背包的思想,\(j\) 需要从大到小枚举。
复杂度 \(O(nk\log n\log k)\),期望得分 \(100\text{pts}\)。
神仙提出的单 \(\log\) 写法:
观察状态的含义:
\(f_{j,k}\) 为 \(1\sim i-1\) 中,被不超过 \(j\) 个修改区间覆盖,结尾 \(\le k\) 的最长不下降子序列的长度。
发现 \(j\) 固定时,\(f_{j,k}\) 随 \(k\) 增加,只增不减。
发现 \(k\) 固定时,\(f_{j,k}\) 随 \(j\) 增加,只增不减。
则树状数组中 \(x\le j,y\le k\) 的最大值,一定会在第 \(j\) 行/ 第 \(k\) 列取到。
考虑建立 \(2\) 个 \(n\) 行的一维树状数组,分别维护每行/每列的 \(f\) 值,更新时更新 整行/整列 有下图形式:
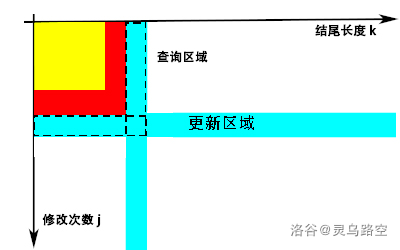
复杂度 \(O(nk\log n)\),期望得分 \(100\text{pts}\)。
代码 P3287 [SCOI2014]方伯伯的玉米田 - Luckyblock
学到了什么
- 修改枚举边界。 P5017 摆渡车
- 删去无用的决策,包括不合法,较劣等情况。 P5017 摆渡车
- 转移时只受相对大小的影响,可考虑记录差值。 P4933 大师,P5664 Emiya 家今天的饭
- 观察单调性,使用单调队列进行优化P5858 「SWTR-03」Golden Sword,P1973 [NOI2011]NOI 嘉年华 还可用于减去无用状态 P3287 [SCOI2014]方伯伯的玉米田。
- 如果数据范围较小或 有特殊性质,可考虑直接暴力枚举进行转移。P5664 Emiya 家今天的饭,P1973 [NOI2011]NOI 嘉年华,P2051 [AHOI2009]中国象棋。二叉树转移时可直接枚举左右儿子。 P1270 “访问”美术馆
- 对一类排序问题可先考虑两个元素的关系,再进行推广。 P2577 [ZJOI2005]午餐
- 注意补集转换。P2577 [ZJOI2005]午餐
- 考虑同类元素贡献合并。P4158 [SCOI2009]粉刷匠
- 不满足单调性可考虑线段树维护。P1295 [TJOI2011]书架
- 区间修改考虑差分。 CF79D Password
- 中序遍历 = 拍扁序。 其每一个子序列 都表示 树联通的一部分。P1040 加分二叉树
- 防止重复更新,考虑倒序枚举。P1273 有线电视网,P3287 [SCOI2014]方伯伯的玉米田
- 形式优美时,可直接用数据结构维护 DP 数组。P3287 [SCOI2014]方伯伯的玉米田
来源:oschina
链接:https://my.oschina.net/u/4267539/blog/4387331