德国数学家David Hilbert在1891年构造了一种曲线,首先把一个正方形等分成四个小正方形,依次从西北角的正方形中心出发往南到西南正方形中心,再往东到东南角的正方形中心,再往北到东北角正方形中心,这是一次迭代;如果对四个小正方形继续上述过程,往下划分,反复进行,最终就得到一条可以填满整个正方形的曲线,这就是Hibert曲线。其生成过程如图1所示。
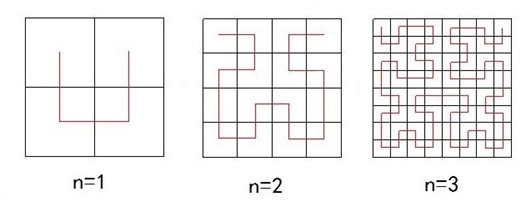
图1 Hilbert曲线的生成
Hilbert曲线可以采用递归过程实现,在递归处理时,连接中点的方式有4种,如图2所示。
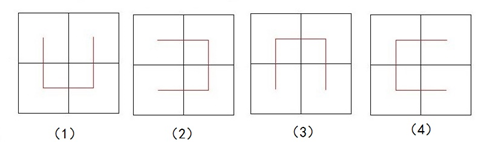
图2 连接中心点的4种方式
设正方形左上角的顶点坐标为(x1,y1),右下角顶点坐标为(x2,y2)。若将方式(3)的正方形左上角坐标置为(x2,y2),右下角坐标置为(x1,y1),则方式(3)等同于方式(1),相当于旋转180°;同理,方式(4)等同于方式(2)。因此,4种连接中心点的方式可以看成(1)和(2)两种。
两种连线方式的连线走向及下一次扩展的方式如图3所示。

图3 两种连线方式走向及扩展
其中,方式(1)的四个中心点坐标分别为:
①(x1+dx/4,y1+dy/4) ②(x1+dx/4, y1+3*dy/4)
③ (x1+3*dx/4, y1+3*dy/4) ④(x1+3*dx/4,y1+dy/4) (dx=x2-1,dy=y2-y1)
方式(2)的四个中心点坐标分别为:
①(x1+dx/4,y1+dy/4) ②(x1+3*dx/4,y1+dy/4)
③ (x1+3*dx/4, y1+3*dy/4) ④(x1+dx/4, y1+3*dy/4)
为此,引入一个标识变量s,s=1表示方式(1),s=-1表示方式(2),这样两种方式的中心点坐标可以统一表示为:
①(x1+dx/4,y1+dy/4) ②(x1+(2-s)*dx/4, y1+(2+s)*dy/4)
③(x1+3*dx/4, y1+3*dy/4) ④(x1+(2+s)*dx/4,y1+(2-s)*dy/4)
递归扩展时,方式(1)中4个小正方形的扩展方式分别是:方式(2)、方式(1)、方式(1)和方式(4)(注意:给定两个顶点坐标顺序调整后等同于方式(2));方式(2)中4个小正方形的扩展方式分别是:方式(1)、方式(2)、方式(2)和方式(3)。
编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>Hilbert曲线</title>
</head>
<body>
<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var depth=5;
ctx.lineWidth = 2;
ctx.strokeStyle = "red";
ctx.beginPath();
ctx.moveTo(50+400/Math.pow(2,depth+1),50+400/Math.pow(2,depth+1));
drawShapes(depth,1,50,50,450,450);
ctx.stroke();
function drawShapes(n,s,x1,y1,x2,y2)
{
dx = x2 - x1,
dy = y2 - y1;
if (n>1)
{
if(s>0)
{
drawShapes(n-1,-1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,1,x1,(y1+y2)/2,(x1+x2)/2,y2);
drawShapes(n-1,1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,-1,x2,(y1+y2)/2,(x1+x2)/2,y1);
}
else
{
drawShapes(n-1,1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,y1,x2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,1,(x1+x2)/2,y2,x1,(y1+y2)/2);
}
}
if (n==1)
{
ctx.lineTo(x1+dx/4,y1+dy/4);
ctx.lineTo(x1+(2-s)*dx/4, y1+(2+s)*dy/4);
ctx.lineTo(x1+3*dx/4, y1+3*dy/4);
ctx.lineTo(x1+(2+s)*dx/4,y1+(2-s)*dy/4);
}
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出如图4所示的Hilbert曲线。

图4 递归深度maxdepth =5的Hilbert曲线
上面的程序需要推出方式(一)和方式(二)的坐标统一形式,还需注意方式(3)和方式(4)与方式(一)和方式(二)的同一性。
由于Hilbert曲线可以看成是4种方式进行组合,因此可以直接对4种方式编写递归过程。编写如下的HTML文件。
<!DOCTYPE html>
<head>
<title>Hilbert曲线</title>
</head>
<body>
<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
ctx.lineWidth = 2;
ctx.strokeStyle = "red";
ctx.beginPath();
var depth=5; // 递归深度
var h=400/Math.pow(2,depth);
var x = 50+h;
var y = 50+h;
ctx.moveTo(x,y);
One(depth);
ctx.stroke();
function One(n) // 方式(1)的递归调用
{
if(n > 0)
{
Two(n-1);
ctx.lineTo(x, y+h); y+=h;
One(n-1);
ctx.lineTo(x+h, y); x+=h;
One(n-1);
ctx.lineTo(x, y-h); y-=h;
Four(n-1);
}
}
function Two(n) // 方式(2)的递归调用
{
if(n > 0)
{
One(n-1);
ctx.lineTo(x+h, y); x+=h;
Two(n-1);
ctx.lineTo(x, y+h); y+=h;
Two(n-1);
ctx.lineTo(x-h, y); x-=h;
Three(n-1);
}
}
function Three(n) // 方式(3)的递归调用
{
if(n > 0)
{
Four(n-1);
ctx.lineTo(x, y-h); y-=h;
Three(n-1);
ctx.lineTo(x-h, y); x-=h;
Three(n-1);
ctx.lineTo(x, y+h); y+=h;
Two(n-1);
}
}
function Four(n) // 方式(4)的递归调用
{
if(n > 0)
{
Three(n-1);
ctx.lineTo(x-h,y); x-=h;
Four(n-1);
ctx.lineTo(x, y-h); y-=h;
Four(n-1);
ctx.lineTo(x+h, y); x+=h;
One(n-1);
}
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出如图5所示的Hilbert曲线。

图5 调用One(depth)时绘制的图形
将程序中的调用语句“One(depth)”改写成“Two(depth)”,则在浏览器窗口中绘制出如图6所示的Hilbert曲线。这个图形可以看成是图5向左旋转90°得到的。实际上,由图2可知,将方式(一)的图形向左旋转90°得到的就是方式(二)的图形。

图6 调用Two(depth)时绘制的图形
将程序中调用语句“One(depth)”改写成“Three(depth)”,同时修改初始坐标为
“var x = 450-h; var y = 450-h;”,则在浏览器窗口中绘制出如图7所示的Hilbert曲线。

图7 调用THree(depth)时绘制的图形
将程序中调用语句“One(depth)”改写成“Four(depth);”,同时修改初始坐标为
“var x = 450-h; var y = 450-h;”,则在浏览器窗口中绘制出如图8所示的Hilbert曲线。

图8 调用Four(depth)时绘制的图形
将Hilbert曲线的生成过程进行动画展示,编写如下的HTML代码。
<!DOCTYPE>
<html>
<head>
<title>Hilbert曲线</title>
</head>
<body>
<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;"></canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var depth=1;
function drawShapes(n,s,x1,y1,x2,y2)
{
dx = x2 - x1,
dy = y2 - y1;
if (n>1)
{
if(s>0)
{
drawShapes(n-1,-1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,1,x1,(y1+y2)/2,(x1+x2)/2,y2);
drawShapes(n-1,1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,-1,x2,(y1+y2)/2,(x1+x2)/2,y1);
}
else
{
drawShapes(n-1,1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,y1,x2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,1,(x1+x2)/2,y2,x1,(y1+y2)/2);
}
}
if (n==1)
{
ctx.lineTo(x1+dx/4,y1+dy/4);
ctx.lineTo(x1+(2-s)*dx/4, y1+(2+s)*dy/4);
ctx.lineTo(x1+3*dx/4, y1+3*dy/4);
ctx.lineTo(x1+(2+s)*dx/4,y1+(2-s)*dy/4);
}
}
function go()
{
ctx.clearRect(0,0,canvas.width,canvas.height);
ctx.lineWidth = 2;
ctx.strokeStyle = "red";
ctx.beginPath();
ctx.moveTo(50+400/Math.pow(2,depth+1),50+400/Math.pow(2,depth+1));
drawShapes(depth,1,50,50,450,450);
ctx.stroke();
depth++;
if (depth>6)
{
depth=1;
}
}
window.setInterval('go()', 1000);
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中呈现出如图9所示的Hilbert曲线动态生成效果。

图9 Hilbert曲线动态生成
来源:oschina
链接:https://my.oschina.net/u/4269975/blog/4338333