数据结构与算法之美_38_分治算法：谈一谈大规模计算框架MapReduce中的分治思想

MapReduce 是 Google 大数据处理的三驾马车之一，另外两个是 GFS 和 Bigtable。它在倒排索引、PageRank 计算、网页分析等搜索引擎相关的计数中都有大量的应用。

MapReduce 的本质就是分治算法。

如何理解分治算法？

分支算法（divide and conquer）的核心思想就是，分而治之，也就是将原问题划分成 n 个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，然后在合并其结果，就得到原问题的解了。

这个定义看起来有点类似递归的定义。关于分支与递归的区别，分支算法是一种处理问题的思想，递归是一种编程技巧。实际上，分治算法一般都比较适合用帝归来实现的。

分治算法的递归实现中，每一层递归都会涉及这样三个操作：

分解：将原问题分解成一系列子问题；
解决：递归地求解各个子问题，若子问题足够小，则直接求解；
合并：将子问题的结果合并成原问题。

分治算法能解决的问题，一般需要满足下面这几个条件：

原问题与分解成的小问题有相同的模式；
原问题分解成的子问题可以独立求解，子问题之间没有相关性，这一点是分治算法跟动态规划的明显区别；
具有分解终止条件，也就是说，当问题足够小时，可以直接求解；
可以将子问题合并成原问题，而这个合并操作的复杂度不能太高，否则就起不到减小算法总体复杂度的效果了。

分支算法应用举例分析

我们通过用分治算法来解决我们在学习排序的时候涉及的一个问题，加深你对分治算法的理解。

排序算法中的数据有有序度、逆序度的概念。我们用有序度来表示一组数据的有序程度，用逆序度来表示一组数据的无序程度。

假设我们有 n 个数据，我们期望数据从小到大排列，那完全有序的数据的有序度就是 n(n-1)/2，逆序度等于 0；相反，倒序排列的数据的有序度就是 0，逆序度是 n(n-1)/2。除了这两种极端情况，我们通过计算有序对或者逆序对的个数，来表示数据的有序度或逆序度。

那如何用编程求出一组数据的有序对个数或者逆序对个数呢？因为有序对个数和逆序对个数的求解方式是类似的，所以我们只思考逆序对个数的求解方法。

最笨的方法，拿每个数字跟它后面的数组比较，看有几个比它小的。我们把它小的数字个数记作 k，通过这样的方式，把每个数字都考察一遍之后，然后对每个数字对应的 k 值求和，最后得到的总和就是逆序对的个数。不过，这样的操作时间复杂度是 O(n^2)。我们希望用更加高效的处理方法。

我们用分治算法来试试。套用分治的思想求数组 A 的逆序对个数。我们可以将数组分成前后两半 A1 和 A2，分别计算 A1 和 A2 的逆序对个数 K1 和 K2，然后再计算 A1 与 A2 之间的逆序对个数 K3。那数组 A 的逆序对个数就等于 K1 + K2 + K3。

使用分治算法的其中一个要求是，子问题合并的代价不能太大，否则就起不了降低时间复杂度的效果了。那回到这个问题，如何快速计算出两个子问题 A1 与 A2 之间的逆序对个数呢？

这就要借助归并排序算法了。

归并排序中有一个非常关键的操作，就是将两个有序的小数组，合并成一个有序的数组。实际上，这个个合并的过程中，我们就可以计算这两个小数组的逆序对个数了。每次合并操作，我们都计算逆序对个数，把这些计算出来的逆序对个数求和，就是这个数组的逆序对个数。

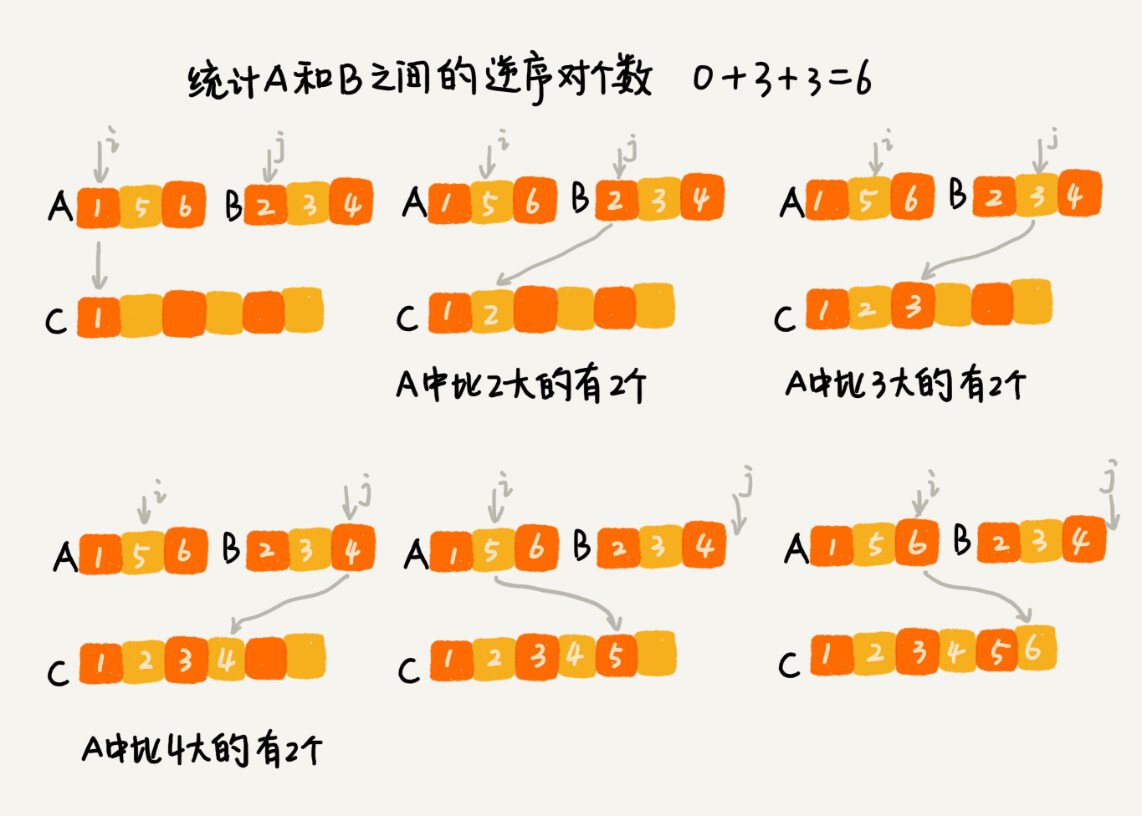
代码如下。

// 全局变量或者成员变量
private int num = 0;

public int count(int[] a, int n){
    num = 0;
    mergeSortCounting(a, 0, n-1);
    return num;
}

private void mergeSortCounting(int[] a, int p, int r){
    if(p &gt;= r){
        return;
    }
    int q = (p + r) / 2;
    mergeSortCount(a, p, q);
    mergeSortCount(a, q+1, r);
    merge(a, p, q, r);
}

private void merge(int[] a, int p, int q, int r){
    int i = p;
    int j = q + 1;
    int k = 0;
    int[] tmp = new int[r-p+1];
    
    while(i &lt;= q &amp;&amp; j &lt;= r){
        if(a[i] &lt;= a[j]){
            tmp[k++] = a[i++];
        }else{
            // 统计 p-q 之间，比 a[j] 大的元素个数
            num += (q - i + 1);
            tmp[k++] = a[j++];
        }
    }
    
    // 处理剩下的
    while(i &lt;= q){
        tmp[k++] = a[i++];
    }
    
    while(j &lt;= r){
        tmp[k++] = a[j++];
    }
    
    for(i = 0; i &lt;= r - q; i++){
        a[p+i] = tmp[i];
    }
}

关于分支算法，还有两个比较经典的问题，可以练习下。

二维平面上有 n 个点，如何快速计算出两个距离最近的点对？
有两个 n * n 的矩阵 A，B，如何快速求解两个矩阵的乘积 C = A * B ？

分支思想的海量数据处理中的应用

分治算法思想的应用非常广泛，并不仅限于指导编程和算法设计。它还经常用在海量数据处理的场景中。

我们前面学习的数据结构和算法，大部分都是基于内存存储和单机处理。但是，如果要处理的数据量非常大，没法一次性放到内存中，这时候，这些数据结构就无法工作了。

比如，给 10GB 的订单文件按照金额排序这样一个需求，看似是简单的排序问题，但是因为数据量太大，有 10GB，而我们的机器的内存可能只有 2、3GB，无法一次性加载到内存，也发通过单纯的使用快排、归并等算法来解决。

要解决这种数据量大到内存装不下的问题，我们就可以利用分治思想。我们可以将海量的数据集合根据某种方法（比如哈希分片取模），划分为几个小的数据集合，每个小的数据集合单独加载到内存中解决，然后再将小数据集合合并成大数据集合。实际上，利用这种分支的处理思想，不仅仅能克服内存的限制，还能利用多线程或者多级处理，加快处理的速度。

比如刚才讲的例子，给 10GB 的订单排序，我们可以先扫描一遍订单，根据订单的金额，将 10GB 的文件划分为几个金额区间。比如订单金额为 1 到 100 元的放到一个小文件，101 到 200 之间的放到另一个文件，以此类推。每个小文件都可以单独加载到内存中进行排序，最后将这些有序的小文件合并，就是最终有序的 10GB 订单数据了（合并多个有序小文件，参考第 29 节堆的应用）。

如果订单数据存储在类似 GFS 这样的分布式系统上，当 10GB 的订单被划分成多个小文件的时候，每个文件可以并行加载到多台机器上处理，最后再将结果合并在一起，这样并行处理的速度也加快了很多。不过，这里有一点需要注意，就是数据的存储与计算所在的机器是同一个网络或者网络中靠的近的（比如一个局域网内，数据存储速度很快），否则就会因为数据访问的速度，导致整个处理过程不但不会变快，反而有可能变慢。

在学习第 23 节哈希算在分布式系统中的应用和第29 节堆的应用中，有很多例子都用到了分治思想来解决问题。

解决开篇

为什么说 MapReduce 的本质就是分治思想呢？

刚才举的订单排序的例子，数据有 10GB 大小，可能给你感受还不够强烈。那如果处理的数据是 1T、10T、100T 这样的，那一台机器处理的效率肯定是非常低的。而对于谷歌搜索引擎来说，网页爬取、清洗、分析、分词、计算权重、倒排索引等等各个环节中，都会面临如此海量的数据（比如网页）。所以，利用集群并行处理显然是大势所趋。

一台机器过于低效，那我们就把任务拆分到多台机器上来处理。如果拆分之后的小任务之间互不干扰，独立计算，最后再将结果合并，这就是分治思想！

实际上，MapReduce 框架只是一个任务调度器，底层依赖 GFS 来存储数据，依赖 Borg 管理机器。它从 GFS 中拿数据，交给 Borg 中的机器执行，并且时刻监控机器执行的进度，一旦出现机器宕机、进度卡壳等，就重新从 Borg 中调度一台机器执行。

尽管 MapReduce 的模型非常简单，但是在 Google 内存应用非常广泛。它除了可以用来处理这种数据与数据之间存在关系的任务，比如 MapReduce 的经典例子，统计文件中单词出现的频率。除此之外，它还可以用来处理数据与数据之间没有关系的任务，比如对网页分析、分词等，每个网页可以独立的分析、分词，而这两个网页之间并没有关系。网页几十亿、上百亿，如果单机处理，效率低下。我们就可以利用 MapReduce 提供的高可靠、高性能、高容错的并行计算框架，并行地吹着几十亿、上百亿的网页。