Like SVMs, Decision Trees are versatile Machine Learning algorithms that can perform both classification and regression tasks, and even multioutput tasks. They are very powerful algorithms, capable of fitting complex datasets. For example, in (https://blog.csdn.net/Linli522362242/article/details/103587172) you trained a DecisionTreeRegressor model on the California housing dataset, fitting it perfectly (actually overfitting it).
Decision Trees are also the fundamental components of Random Forests, which are among the most powerful Machine Learning algorithms available today.
we will start by discussing how to train, visualize, and make predictions with Decision Trees. Then we will go through the CART training algorithm used by Scikit-Learn, and we will discuss how to regularize trees and use them for regression tasks. Finally, we will discuss some of the limitations of Decision Trees.
Training and Visualizing a Decision Tree
To understand Decision Trees, let's just build one and take a look at how it makes predictions. The following code trains a DecisionTreeClassifier on the iris dataset:
###############################
# At first, we have to install graphviz by using pip3 install graphviz
#Then, go to website "https://graphviz.gitlab.io/_pages/Download/Download_windows.html"
to download .msi file, and install it and write down the directory where you install it 
# next step, we have to append it to system environment path
#On jupyter notebook, you have to append the following codes:
import os
os.environ["PATH"] += os.pathsep + "D:/Graphviz2.38/bin" # " directory" where you intall graphviz
https://www.cnblogs.com/Leo-Xia/p/9947302.html
###############################
The following code trains a DecisionTreeClassifier on the iris dataset
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:,2:] #petal length and width
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42) #2 floors
tree_clf.fit(X,y)
iris.keys()
You can visualize the trained Decision Tree by first using the export_graphviz() method to output a graph definition file called iris_tree.dot:
# pip3 install graphviz
from graphviz import Source
from sklearn.tree import export_graphviz
import os
os.environ["PATH"] += os.pathsep + "D:/Graphviz2.38/bin" # " directory" where you intall graphviz
export_graphviz(
tree_clf,
out_file = os.path.join( "iris_tree.dot"),
feature_names = iris.feature_names[2:], ###
class_names = iris.target_names,###
rounded = True,
filled = True
)
Source.from_file("iris_tree.dot")
Figure 6-1. Iris Decision Tree
#########################################################################
https://blog.csdn.net/Linli522362242/article/details/104124771
Gini impurity
Used by the CART (Classification And Regression Tree) algorithm for classification trees, Gini impurity is a measure of how often a randomly chosen element from the set would be incorrectly labeled if it was randomly labeled according to the distribution of labels in the subset. The Gini impurity can be computed by summing the probability 
of an item with label i being chosen times the probability 
of a mistake in categorizing that item. It reaches its minimum (zero) when all cases in the node fall into a single target category.
To compute Gini impurity for a set of items with 
classes, suppose 
, and let be the fraction of items labeled with class 
in the set.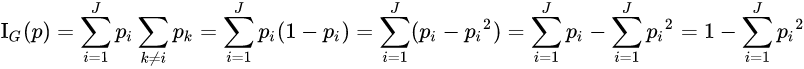
: the sum of all probabilities of all classes(J) is equal to 1.
example: 
and 1 == 
+ 
+ 
#########################################################################
Making Predictions
Let’s see how the tree represented in Figure 6-1 makes predictions. Suppose you find an iris flower and you want to classify it. You start at the root node (depth 0, at the top): this node asks whether the flower’s petal length is smaller than 2.45 cm. If it is, then you move down to the root’s left child node (depth 1, left). In this case, it is a leaf node (i.e., it does not have any children nodes), so it does not ask any questions: you can simply look at the predicted class for that node and the Decision Tree predicts that your flower is an Iris-Setosa (class=setosa).
Now suppose you find another flower, but this time the petal length is greater than 2.45 cm. You must move down to the root’s right child node (depth 1, right), which is not a leaf node, so it asks another question: is the petal width smaller than 1.75 cm? If it is, then your flower is most likely an Iris-Versicolor (depth 2, left). If not, it is likely an Iris-Virginica (depth 2, right). It’s really that simple.
#################################
NOTE
One of the many qualities of Decision Trees is that they require very little data preparation. In particular, they don’t require feature scaling or centering at all.
#################################
A node’s samples attribute counts how many training instances it applies to. For example, 100 training instances have a petal width greater than 2.45 cm (depth 1, right), among which 54 have a petal width smaller than 1.75 cm (depth 2, left). A node’s value attribute tells you how many training instances of each class this node applies to: for example, the bottom-right node applies to 0 Iris-Setosa, 1 Iris-Versicolor, and 45 Iris-Virginica. Finally, a node’s gini attribute measures its impurity不纯: a node is “pure” (gini=0) if all training instances it applies to belong to the same class. For example, since the depth-1 left node applies only to Iris-Setosa training instances, it is pure and its gini score is 0. Equation 6-1 shows how the training algorithm computes the gini score 
of the ith node. For example, the depth-2 left node has a gini score equal to . Another impurity measure is discussed shortly.
Equation 6-1. Gini impurity
is the ratio of class k instances among the training instances in the 
node/region.
#################################
NOTE
Scikit-Learn uses the CART algorithm, which produces only binary trees: nonleaf nodes always have two children (i.e.,
questions only have yes/no answers). However, other algorithms such as ID3 can produce Decision Trees with nodes that have more than two children.
#################################
from matplotlib.colors import ListedColormap
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
x1s = np.linspace( axes[0], axes[1], 100 )
x2s = np.linspace( axes[2], axes[3], 100 )
x1, x2 = np.meshgrid( x1s, x2s )
X_new = np.c_[ x1.ravel(), x2.ravel() ]
y_pred = clf.predict( X_new ).reshape( x1.shape )
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf( x1, x2, y_pred, alpha=0.3, cmap=custom_cmap )
# if not iris:
# custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
# plt.contour( x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8 )
if plot_training:
plt.plot( X[:,0][y==0], X[:,1][y==0], "yo", label="Iris setosa" )
plt.plot( X[:,0][y==1], X[:,1][y==1], "bs", label="Iris versicolor")
plt.plot( X[:,0][y==2], X[:,1][y==2], "g^", label="Iris virginica")
plt.axis(axes)
if iris:
plt.xlabel( "Petal length", fontsize=14 )
plt.ylabel( "Petal width", fontsize=14 )
else:
plt.xlabel( r"$x_1$", fontsize=18 )
plt.ylabel( r"$x_2$", fontsize=18, rotation=0 )
# if legend:
# plt.legend( loc="lower right", fontsize=14 )
plt.figure( figsize=(8,4) )
plot_decision_boundary( tree_clf, X,y )
plt.plot( [2.45, 2.45], [0, 3], "k-", linewidth=2 ) # Depth=0
plt.plot( [2.45, 7.5], [1.75, 1.75], "k--", linewidth=2) # Depth=1
plt.plot( [4.95, 4.95], [0, 1.75], "k:", linewidth=2) # Depth=2
plt.plot( [4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.3, 1.0, "Depth=0", fontsize=15)
plt.text(3.2, 1.8, "Depth=1", fontsize=13)
plt.text(4.0, 0.5, "(Depth=2)", fontsize=11)
plt.show()
Figure 6-2. Decision Tree decision boundaries
Figure 6-2 shows this Decision Tree’s decision boundaries. The thick vertical line represents the decision boundary of the root node (depth 0): petal length = 2.45 cm. Since the left area is pure (only Iris-Setosa), it cannot be split any further. However, the right area is impure, so the depth-1 right node splits it at petal width = 1.75 cm (represented by the dashed line). Since max_depth was set to 2, the Decision Tree stops right there. However, if you set max_depth to 3, then the two depth-2 nodes would each add another decision boundary (represented by the dotted lines).
###############################################################
Model Interpretation: White Box Versus Black Box
As you can see Decision Trees are fairly intuitive and their decisions are easy to interpret.
Such models are often called white box models. In contrast, as we will see, Random Forests or neural networks are generally considered black box models. They make great predictions, and you can easily check the calculations that they performed to make these predictions; nevertheless, it is usually hard to explain in simple terms why the predictions were made. For example, if a neural network says that a particular person appears on a picture, it is hard to know what actually contributed to导致 this prediction: did the model recognize that person’s eyes? Her mouth? Her nose? Her shoes? Or even the couch that she was sitting on? Conversely, Decision Trees provide nice and simple classification rules that can even be applied manually if need be (e.g., for flower classification).
###############################################################
Estimating Class Probabilities
A Decision Tree can also estimate the probability that an instance belongs to a particular class k: first it traverses the tree to find the leaf node for this instance, and then it returns the ratio of training instances of class k in this node. For example, suppose you have found a flower whose petals are 5 cm long and 1.5 cm wide. The corresponding leaf node is the depth-2 left node, so the Decision Tree should output the following probabilities: 0% for Iris-Setosa (0/54), 90.7% for Iris-Versicolor (49/54), and 9.3% for Iris-Virginica (5/54). And of course if you ask it to predict the class, it should output Iris-Versicolor (class 1) since it has the highest probability. Let’s check this:
tree_clf.predict_proba([ [5, 1.5] ])
tree_clf.predict([ [5, 1.5] ])
iris.target_names[ tree_clf.predict([ [5, 1.5] ]) ]
Perfect! Notice that the estimated probabilities would be identical anywhere else in the bottom-right rectangle of Figure 6-2—for example, if the petals were 6 cm long and 1.5 cm wide (even though it seems obvious that it would most likely be an Iris-Virginica
in this case).
The CART Training Algorithm
Scikit-Learn uses the Classification And Regression Tree (CART) algorithm to train Decision Trees (also called “growing” trees). The idea is really quite simple: the algorithm first splits the training set in two subsets using a single feature k and a threshold 
(e.g., “petal length ≤ 2.45 cm”). How does it choose k and 
? It searches for the pair (k, 
) that produces the purest subsets (weighted by their size). The cost function that the algorithm tries to minimize is given by Equation 6-2.
Equation 6-2. CART cost function for classification
Once it has successfully split the training set in two, it splits the subsets using the same logic, then the sub-subsets and so on, recursively. It stops recursing once it reaches the maximum depth (defined by the max_depth hyperparameter), or if it cannot find a split that will reduce impurity. A few other hyperparameters (described in a moment) control additional stopping conditions (min_samples_split, min_samples_leaf, min_weight_fraction_leaf, and max_leaf_nodes).
###############################################
WARNING
As you can see, the CART algorithm is a greedy贪婪 algorithm: it greedily searches for an optimum split at the top level, then repeats the process at each level. It does not check whether or not the split will lead to the lowest possible impurity several levels down. A greedy algorithm often produces a reasonably good solution, but it is not guaranteed to be the optimal solution.
###############################################
Unfortunately, finding the optimal tree is known to be an NP-Complete problem: it requires 
time, making the problem intractable难对付的 even for fairly small training sets. This is why we must settle解决 for a “reasonably good”（而不是最佳的) solution.
Computational Complexity
Making predictions requires traversing the Decision Tree from the root to a leaf. Decision Trees are generally approximately balanced, so traversing the Decision Tree requires going through roughly 
nodes（log2 is the binary logarithm. It is equal to 
= log(m) / log(2).）. Since each node(in n) only requires checking the value of one feature, the overall prediction complexity is just , independent of the number of features与特征的数量无关. So predictions are very fast, even when dealing with large training sets.
However, the training algorithm compares all features (or less if max_features is set) on all samples at each node. This results in a training complexity训练时间复杂度 of 
(n-dimensions OR n-features, m numbers of instances). For small training sets (less than a few thousand instances), Scikit-Learn can speed up training by presorting the data (set presort=True), but this slows down training considerably for larger training sets.
Gini Impurity or Entropy?
By default, the Gini impurity measure is used, but you can select the entropy impurity measure instead by setting the criterion标准 hyperparameter to "entropy". The concept of entropy originated in thermodynamics热力学 as a measure of molecular分子 disorder: entropy熵 approaches zero when molecules are still and well ordered当分子井然有序的时候，熵值接近于 0. It later spread to a wide variety of domains, including Shannon's information theory, where it measures the average information content of a message: entropy is zero when all messages are identical. In Machine Learning, it is frequently used as an impurity measure: a set's entropy is zero when it contains instances of only one class. Equation 6-3 shows the definition of the entropy of the ith node. For example, the depth-2 left node in Figure 6-1
has an entropy equal to 
.
Equation 6-3. Entropy
So should you use Gini impurity or entropy? The truth is, most of the time it does not make a big difference: they lead to similar trees. Gini impurity is slightly faster to compute, so it is a good default. However, when they differ, Gini impurity tends to isolate the most frequent class in its own branch of the tree, while entropy tends to produce slightly more balanced trees.
Regularization Hyperparameters正则化超参数
Decision Trees make very few assumptions about the training data (as opposed to linear models, which obviously assume that the data is linear, for example). If left unconstrained如果不添加约束, the tree structure will adapt itself to the training data, fitting it very closely, and most likely overfitting it. Such a model is often called a nonparametric model, not because it does not have any parameters (it often has a lot) but because the number of parameters is not determined prior to training, so the model structure is free to stick closely to the data所以模型结构可以根据数据的特性自由生长.
In contrast, a parametric model such as a linear model has a predetermined number of parameters, so its degree of freedom is limited, reducing the risk of overfitting (but increasing the risk of underfitting).
To avoid overfitting the training data, you need to restrict the Decision Tree's freedom during training. As you know by now, this is called regularization. The regularization hyperparameters depend on the algorithm used, but generally you can at least restrict the maximum depth of the Decision Tree. In Scikit-Learn, this is controlled by the max_depth hyperparameter (the default value is None, which means unlimited). Reducing max_depth will regularize the model and thus reduce the risk of overfitting.
The DecisionTreeClassifier class has a few other parameters that similarly restrict the shape of the Decision Tree: min_samples_split (the minimum number of samples a node must have before it can be split), min_samples_leaf (the minimum number of samples a leaf node must have), min_weight_fraction_leaf (same as min_samples_leaf but expressed as a fraction of the total number of weighted instances), max_leaf_nodes (maximum number of leaf nodes), and max_features (maximum number of features that are evaluated for splitting at each node). Increasing min_* hyperparameters or reducing max_* hyperparameters will regularize the model.
#########################################
NOTE
Other algorithms work by first training the Decision Tree without restrictions, then pruning剪枝 (deleting) unnecessary nodes. A node whose children are all leaf nodes is considered unnecessary if the purity improvement it provides is not statistically significant.
Standard statistical tests, such as the χ2 test, are used to estimate the probability that the improvement is purely the result of chance改进是否纯粹是偶然性的结果 (which is called the null hypothesis). If this probability, called the p-value, is higher than a given threshold (typically 5%, controlled by a hyperparameter也就是 95% 置信度), then the node is considered unnecessary and its children are deleted. The pruning continues until all unnecessary nodes have been pruned.
#########################################
Figure 6-3 shows two Decision Trees trained on the moons dataset (introduced in https://blog.csdn.net/Linli522362242/article/details/104280075). On the left, the Decision Tree is trained with the default hyperparameters (i.e., no restrictions), and on the right the Decision Tree is trained with min_samples_leaf=4. It is quite obvious that the model on the left is overfitting, and the model on the right will probably generalize better.
from sklearn.datasets import make_moons
Xm, ym = make_moons( n_samples=100, noise=0.25, random_state=53 )#X[:, x1 or x2], y[0 or 1]
deep_tree_clf1 = DecisionTreeClassifier( random_state=42 )#with the default hyperparameters
deep_tree_clf2 = DecisionTreeClassifier( min_samples_leaf=4, random_state=42 )
deep_tree_clf1.fit(Xm, ym)
deep_tree_clf2.fit(Xm, ym)
from matplotlib.colors import ListedColormap
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
x1s = np.linspace( axes[0], axes[1], 100 )
x2s = np.linspace( axes[2], axes[3], 100 )
x1, x2 = np.meshgrid( x1s, x2s )
X_new = np.c_[ x1.ravel(), x2.ravel() ]
y_pred = clf.predict( X_new ).reshape( x1.shape )
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf( x1, x2, y_pred, alpha=0.3, cmap=custom_cmap )############
if not iris:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour( x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8 )
if plot_training:
plt.plot( X[:,0][y==0], X[:,1][y==0], "yo", label="Iris setosa" )
plt.plot( X[:,0][y==1], X[:,1][y==1], "bs", label="Iris versicolor")
plt.plot( X[:,0][y==2], X[:,1][y==2], "g^", label="Iris virginica")
plt.axis(axes)
if iris:
plt.xlabel( "Petal length", fontsize=14 )
plt.ylabel( "Petal width", fontsize=14 )
else:
plt.xlabel( r"$x_1$", fontsize=18 )
plt.ylabel( r"$x_2$", fontsize=18, rotation=0 )
if legend:
plt.legend( loc="lower right", fontsize=14 )
fig, axes = plt.subplots( ncols=2, figsize=(16,4), sharey=True )
plt.sca( axes[0] )
plot_decision_boundary( deep_tree_clf1, Xm, ym, axes=[-1.5, 2.4, -1, 1.5], iris=False )
plt.title( "No restrictions", fontsize=16 )
plt.sca( axes[1] )
plot_decision_boundary( deep_tree_clf2, Xm, ym, axes=[-1.5, 2.4, -1, 1.5], iris=False )
plt.title( "min_samples_leaf = {}".format(deep_tree_clf2.min_samples_leaf), fontsize=14 )
plt.ylabel("") #remove the ylabel
plt.show()
Figure 6-3. Regularization using min_samples_leaf(叶节点必须具有的最小样本数)
Regression
Decision Trees are also capable of performing regression tasks. Let's build a regression tree using Scikit-Learn’s DecisionTreeRegressor class, training it on a noisy quadratic dataset with max_depth=2:
# Quadratic training set + noise
np.random.seed(42)
m=200
X = np.random.rand(m,1)
y = 4 * (X-0.5)**2 + np.random.randn(m,1) / 10 # +noise
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X,y)
# pip3 install graphviz
from graphviz import Source
from sklearn.tree import export_graphviz
import os
os.environ["PATH"] += os.pathsep + "D:/Graphviz2.38/bin" # " directory" where you intall graphviz
export_graphviz(
tree_reg1,
out_file = os.path.join("regression_tree.dot"),
feature_names = ["x1"], ###
rounded = True,
filled = True
)
Source.from_file("regression_tree.dot")
Figure 6-4. A Decision Tree for regression
This tree looks very similar to the classification tree you built earlier. The main difference is that instead of predicting a class in each node, it predicts a value. For example, suppose you want to make a prediction for a new instance with x1 = 0.6. You traverse the tree starting at the root, and you eventually reach the leaf node that predicts value=0.111. This prediction is simply the average target value of the 110 training instances associated to this leaf node. This prediction results in a Mean Squared Error (MSE) equal to 0.015 over these 110 instances.
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_reg1.fit(X,y)
tree_reg2.fit(X,y)
def plot_regression_predictions( tree_reg, X,y, axes=[0,1, -0.2,1], ylabel="$y$" ):
x1 = np.linspace( axes[0], axes[1], 500).reshape(-1,1)
y_pred = tree_reg.predict(x1)
plt.axis(axes)
plt.xlabel( "$x_1$", fontsize=18, rotation=0 )
if ylabel:
plt.ylabel(ylabel, fontsize=18, rotation=0)
plt.plot( X, y, "b." )
#the predicted value for each region is always the average target value of the
#instances in that region
plt.plot( x1,y_pred, 'r.-', linewidth=2, label=r"$\hat{y}$" )
fig, axes = plt.subplots(ncols=2, figsize=(10,4), sharey=True)
plt.sca( axes[0] )
plot_regression_predictions(tree_reg1, X,y)
#depth=1 #depth=2 #depth=2
for split, style in ( (0.1973, "y-"), (0.0917, "y--"), (0.7718,"y--") ):
plt.plot( [split, split], [-0.2,1], style, linewidth=2 ) # splitting lines
plt.text(0.21, 0.65, "Depth=0", fontsize=15)
plt.text(0.01, 0.2, "Depth=1", fontsize=13)
plt.text(0.65, 0.8, "Depth=1", fontsize=13)
plt.legend(loc="upper center", fontsize=18)
plt.title("max_depth=2", fontsize=14)
plt.sca( axes[1] )
plot_regression_predictions(tree_reg2, X,y, ylabel=None)
#depth=1 #depth=2 #depth=2
for split, style in ( (0.1973, "y-"), (0.0917, "y--"), (0.7718,"y--") ):
plt.plot( [split, split], [-0.2,1], style, linewidth=2 )# splitting line
for split in (0.0458, 0.1298, 0.2873, 0.9040): #depth=3
plt.plot( [split, split], [-0.2,1], "k:", linewidth=1 ) # splitting lines
plt.text(0.3, 0.5, "Depth=2", fontsize=14)
plt.title("max_depth=3", fontsize=14)
plt.show()
Figure 6-5. Predictions of two Decision Tree regression models
注：图里面的红线就是训练实例的平均目标值，对应上图中的 the predicted value of the instances in that region
This model's predictions are represented on the left of Figure 6-5. If you set max_depth=3, you get the predictions represented on the right. Notice how the predicted value for each region is always the average target value of the instances in that region. The algorithm splits each region in a way that makes most training instances as close as possible to that predicted value. 算法以一种使大多数训练实例尽可能接近该预测值的方式分割每个区域。
The CART algorithm works mostly the same way as earlier, except that instead of trying to split the training set in a way that minimizes impurity, it now tries to split the training set in a way that minimizes the MSE. Equation 6-4 shows the cost function that the algorithm tries to minimize.
Equation 6-4. CART cost function for regression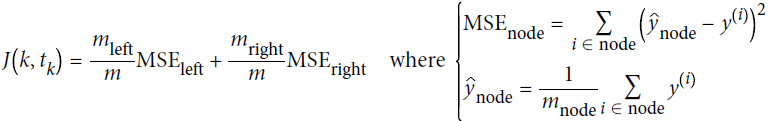
Just like for classification tasks, Decision Trees are prone to overfitting when dealing with regression tasks. Without any regularization (i.e., using the default hyperparameters), you get the predictions on the left of Figure 6-6. It is obviously overfitting the training set very badly. Just setting min_samples_leaf=10 results in a much more reasonable model, represented on the right of Figure 6-6.
tree_reg1 = DecisionTreeRegressor(random_state=42) #Without any regularization and using the default hyperparameters
tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf = 10)
tree_reg1.fit(X,y)
tree_reg2.fit(X,y)
x1 = np.linspace(0,1, 500).reshape(-1,1)
y_pred1 = tree_reg1.predict(x1)
y_pred2 = tree_reg2.predict(x1)
fig, axes = plt.subplots(ncols=2, figsize=(10,4), sharey=True)
plt.sca(axes[0])
plt.plot(X, y, "b.")
plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\hat {y}$" )
plt.axis([0,1,-0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", fontsize=18, rotation=0)
plt.legend(loc="upper center", fontsize=18)
plt.title("No restrictions", fontsize=14)
plt.sca(axes[1])
plt.plot(X, y, "b.")
plt.plot(x1, y_pred2, "r.-", linewidth=2, label=r"$\hat {y}$" )
plt.axis([0,1,-0.2,1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.title("min_samples_leaf={}".format(tree_reg2.min_samples_leaf), fontsize=14)
plt.show()
Figure 6-6. Regularizing a Decision Tree regressor
You get the predictions on the left of Figure 6-6. It is obviously overfitting the training set very badly. Just setting min_samples_leaf=10 results in a much more reasonable model, represented on the right of Figure 6-6
Instability
Hopefully by now you are convinced that Decision Trees have a lot going for them: they are simple to understand and interpret, easy to use, versatile多用途的, and powerful. However they do have a few limitations. First, as you may have noticed, Decision
Trees love orthogonal正交化 decision boundaries (all splits are perpendicular to an axis), which makes them sensitive to training set rotation. For example, Figure 6-7 shows a simple linearly separable dataset: on the left, a Decision Tree can split it easily, while on the right, after the dataset is rotated by 45°, the decision boundary looks unnecessarily convoluted卷曲的/复杂的. Although both Decision Trees fit the training set perfectly, it is very likely that the model on the right will not generalize well. One way to limit this problem is to use PCA, which often results in a better orientation of the training data.
np.random.seed(6)
Xs = np.random.rand(100,2)-0.5# between [0, 1)-0.5
#True/False-->1/0 then times 2 == 2/0
ys = (Xs[:, 0] > 0).astype(np.float32) * 2
Xs[:5]
angle = np.pi/4 #rotaion angle
rotation_maxtrix = np.array([ [np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)] ])
Xsr = Xs.dot( rotation_maxtrix)
Xsr[:5]
tree_clf_s = DecisionTreeClassifier( random_state=42 )
tree_clf_s.fit( Xs,ys )
tree_clf_sr = DecisionTreeClassifier( random_state=42 )
tree_clf_sr.fit( Xsr,ys )
fig, axes = plt.subplots( ncols=2, figsize=(10,4), sharey=True )
plt.sca( axes[0] )
plot_decision_boundary( tree_clf_s, Xs, ys, axes=[-0.7,0.7, -0.7,0.7], iris=False )
plt.sca( axes[1] )
plot_decision_boundary( tree_clf_sr, Xsr, ys, axes=[-0.7,0.7, -0.7,0.7], iris=False)
plt.ylabel("")
plt.subplots_adjust(wspace=0.05)
plt.title("Figure 6-7. Sensitivity to training set rotation")
plt.show()
Figure 6-7. Sensitivity to training set rotation
on the left, a Decision Tree can split it easily, while on the right, after the dataset is rotated by 45°, the decision boundary looks unnecessarily convoluted卷曲的/复杂的. Although both Decision Trees fit the training set perfectly, it is very likely that the model on the right will not generalize well.
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target
angle = np.pi / 180 * 20
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
Xr = X.dot(rotation_matrix)
tree_clf_r = DecisionTreeClassifier(random_state=42)
tree_clf_r.fit(Xr, y)
plt.figure(figsize=(8, 3))
plot_decision_boundary(tree_clf_r, Xr, y, axes=[0.5, 7.5, -1.0, 1], iris=False)
plt.show()
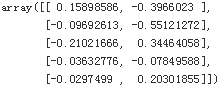
More generally, the main issue with Decision Trees is that they are very sensitive to small variations变化 in the training data. For example, if you just remove the widest Iris-Versicolor from the iris training set (the one with petals 4.8 cm long and 1.8 cm wide) and train a new Decision Tree, you may get the model represented in Figure 6-8. As you can see, it looks very different from the previous Decision Tree (Figure 6-2). Actually, since the training algorithm used by Scikit-Learn is stochastic you may get very different models even on the same training data (unless you set the random_state hyperparameter).
# X[:,1][y==1].max() get the Iris versicolor's the largeist width
X[ ( X[:, 1]== X[:,1][y==1].max() )&(y==1) ] # the widest Iris versicolor((y==1)) flower's attributes value
not_widest_versicolor = (X[:,1]!=1.8) | (y==2) #Iris' width !=1.8 for ignoring the widest Versicolor or Virginica(y==2)
X_tweaked = X[not_widest_versicolor]
y_tweaked = y[not_widest_versicolor]
tree_clf_tweaked = DecisionTreeClassifier( max_depth=2, random_state=40 )
tree_clf_tweaked.fit(X_tweaked, y_tweaked)
plt.figure( figsize=(8,4) )
plot_decision_boundary( tree_clf_tweaked, X_tweaked, y_tweaked, legend=False)
plt.plot( [0,7.5], [0.8,0.8], 'k-', linewidth=2 )
plt.plot( [0,7.5], [1.75,1.75], 'k--', linewidth=2 )
plt.text(1.0,0.9, "Depth=0", fontsize=15)
plt.text(1.0,1.8, "Depth=1", fontsize=13)
plt.show()
Figure 6-8. Sensitivity to training set details
Random Forests can limit this instability by averaging predictions over many trees.
Exerciseshttps://quizlet.com/293807138/final-ml-flash-cards/
1. What is the approximate depth of a Decision Tree trained (without restrictions) on a training set with 1 million (
) instances?
The depth of a well-balanced binary tree containing m leaves is equal to 
, rounded up. A binary Decision Tree (one that makes only binary decisions, as is the case of all trees in Scikit-Learn) will end up more or less well balanced at the end of training, with one leaf per training instance if it is trained without restrictions. Thus, if the training set contains one million instances, the Decision Tree will have a depth of 
≈ 20 (actually a bit more since the tree will generally not be perfectly well balanced).
2. Is a node's Gini impurity generally lower or greater than its parent's? Is it generally lower/greater, or always lower/greater?
Equation 6-1. Gini impurity is the ratio of class k instances among the training instances in the node/region.
probabilities: 0% for Iris-Setosa (0/54), 90.7% for Iris-Versicolor (49/54), and 9.3% for Iris-Virginica (5/54)
<0.5 #A node's Gini impurity is generally lower than its parent's(0.5).
=0.02119230769230769230769230769231
Equation 6-4. CART cost function for regression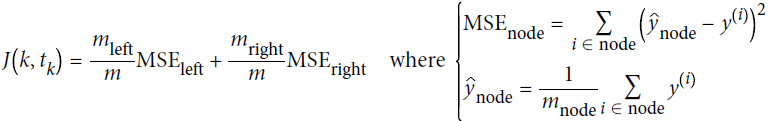
A node's Gini impurity is generally lower than its parent's. This is due to the CART training algorithm's cost function, which splits each node in a way that minimizes the weighted sum of its children's Gini impurities. However, it is possible for a node to have a higher Gini impurity than its parent, as long as this increase is more than compensated for by a decrease of the other child's impurity. For example, consider a node containing four instances of class A and 1 of class B. Its Gini impurity is 
= 0.32. Now suppose the dataset is one-dimensional and the instances are lined up in the following order: A, B, A, A, A. You can verify that the algorithm will split this node after the second instance, producing one child node with instances A, B, and the other child node with instances A, A, A. The first child node's Gini impurity is 
= 0.5(>0.32), which is higher than its parent. This is compensated for by the fact that the other node is pure(Gini impurity=0), so the overall weighted Gini impurity is 
= 0.2 , which is lower than the parent's Gini impurity.
3. If a Decision Tree is overfitting the training set, is it a good idea to try decreasing max_depth?
If a Decision Tree is overfitting the training set, it may be a good idea to decrease max_depth, since
this will constrain the model, regularizing it(Reducing max_depth will regularize the model and thus reduce the risk of overfitting.).???
4. If a Decision Tree is underfitting the training set, is it a good idea to try scaling the input features?
Decision Trees don’t care whether or not the training data is scaled or centered; that’s one of the nice things about them. So if a Decision Tree underfits the training set, scaling the input features will just be a waste of time.
5. If it takes one hour to train a Decision Tree on a training set containing 1 million instances, roughly how much time will it take to train another Decision Tree on a training set containing 10 million instances?
The computational complexity of training a Decision Tree is O(n × m log(m)). So if you multiply the training set size by 10, the training time will be multiplied by K = (n × 10m × log(10m)) / (n × m × log(m)) = 10 × log(10m) / log(m). If m = 
then K ≈ 11.7( 10*7log10 / 6log10 ==70/6 ), so you can expect the training time to be roughly 11.7 hours.
6. If your training set contains 100,000 instances, will setting presort=True speed up training?
Presorting the training set speeds up training only if the dataset is smaller than a few thousand instances. If it contains 100,000 instances, setting presort=True will considerably slow down training.
7. Train and fine-tune a Decision Tree for the moons dataset.
a. Generate a moons dataset using make_moons(n_samples=10000, noise=0.4).
from sklearn.datasets import make_moons
X,y = make_moons(n_samples=10000, noise=0.4, random_state=42)
b. Split it into a training set and a test set using train_test_split().
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, random_state=42)
c. Use grid search with cross-validation (with the help of the GridSearchCV class) to find good hyperparameter values for a DecisionTreeClassifier. Hint: try various values for max_leaf_nodes.
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier
params = { 'max_leaf_nodes': list(range(2,100)), 'min_samples_split':[2,3,4] }
grid_search_cv = GridSearchCV( DecisionTreeClassifier(random_state=42), params, verbose=1, cv=3 )
grid_search_cv.fit(X_train, y_train)
grid_search_cv.best_estimator_
d. Train it on the full training set using these hyperparameters, and measure your model’s performance on the test set. You should get roughly 85% to 87% accuracy.
By default, GridSearchCV trains the best model found on the whole training set (you can change this by setting refit=False), so we don't need to do it again. We can simply evaluate the model's accuracy:
from sklearn.metrics import accuracy_score
y_pred = grid_search_cv.predict(X_test)
accuracy_score(y_test, y_pred)
8. Grow a forest.
a. Continuing the previous exercise, generate 1,000 subsets of the training set, each containing 100 instances selected randomly. Hint: you can use Scikit- Learn’s ShuffleSplit class for this.
from sklearn.model_selection import ShuffleSplit
#n_samples=10000
#test_size=0.2 len(X_test)=2000 len(X_train)=8000
n_trees = 1000
n_instances = 100
mini_sets = []
#len(variation set OR test_size)=8000-100=7900 then sub_training set size=100
rs = ShuffleSplit(n_splits=n_trees, test_size=len(X_train)- n_instances, random_state=42)
for mini_train_index, mini_test_index in rs.split(X_train):
X_mini_train = X_train[mini_train_index] #length=100
y_mini_train = y_train[mini_train_index]
mini_sets.append( (X_mini_train,y_mini_train) )
b. Train one Decision Tree on each subset, using the best hyperparameter values found above. Evaluate these 1,000 Decision Trees on the test set. Since they were trained on smaller sets, these Decision Trees will likely perform worse than the first Decision Tree, achieving only about 80% accuracy.
from sklearn.base import clone
forest = [ clone(grid_search_cv.best_estimator_) for _ in range(n_trees) ] #length==1000
forest[:3]
accuracy_scores = []
for tree, (X_mini_train, y_mini_train) in zip(forest, mini_sets):
tree.fit(X_mini_train, y_mini_train)
y_pred = tree.predict(X_test)
accuracy_scores.append( accuracy_score(y_test, y_pred) )
np.mean( accuracy_scores )
Since they were trained on smaller sets(size=100), these Decision Trees will likely perform worse than the first Decision Tree, achieving only about 80% accuracy.
c. Now comes the magic. For each test set instance, generate the predictions of the 1,000 Decision Trees, and keep only the most frequent prediction (you can use SciPy’s mode() function for this). This gives you majority-vote predictions over the test set.
# n_trees = 1000
Y_pred = np.empty( [n_trees, len(X_test)], dtype=np.uint8 ) #(1000, 2000)
for tree_index, tree in enumerate(forest):
Y_pred[tree_index] = tree.predict(X_test)
from scipy.stats import mode
y_pred_majority_votes, n_votes = mode(Y_pred, axis=0)
y_pred_majority_votes, n_votes
d. Evaluate these predictions on the test set: you should obtain a slightly higher accuracy than your first model (about 0.5 to 1.5% higher). Congratulations, you have trained a Random Forest classifier!
accuracy_score( y_test, y_pred_majority_votes.reshape([-1]) )
来源：CSDN
作者：LIQING LIN
链接：https://blog.csdn.net/Linli522362242/article/details/104542381