matlab dct2和fft2变换的系数分布(BM3D滤波时，相似块分组的阈值凭据）

clear;
woman=imread('C:\Users\ThinkPad\Pictures\lena.jpg');

X=mat2gray(woman);

noise=randn(size(X));

sigma=0.1;
X=X+noise*sigma;

%进行dct2变换
DCT=dct2(X);

%进行fft变换
FFT=fft2(X);


figure
subplot(2,1,1)
%查看DCT系数分布情况
histogram(DCT);
title('DCT系数分布情况');

subplot(2,1,2)
%查看FFT系数分布情况
histogram(real(FFT));
title('FFT系数分布情况');

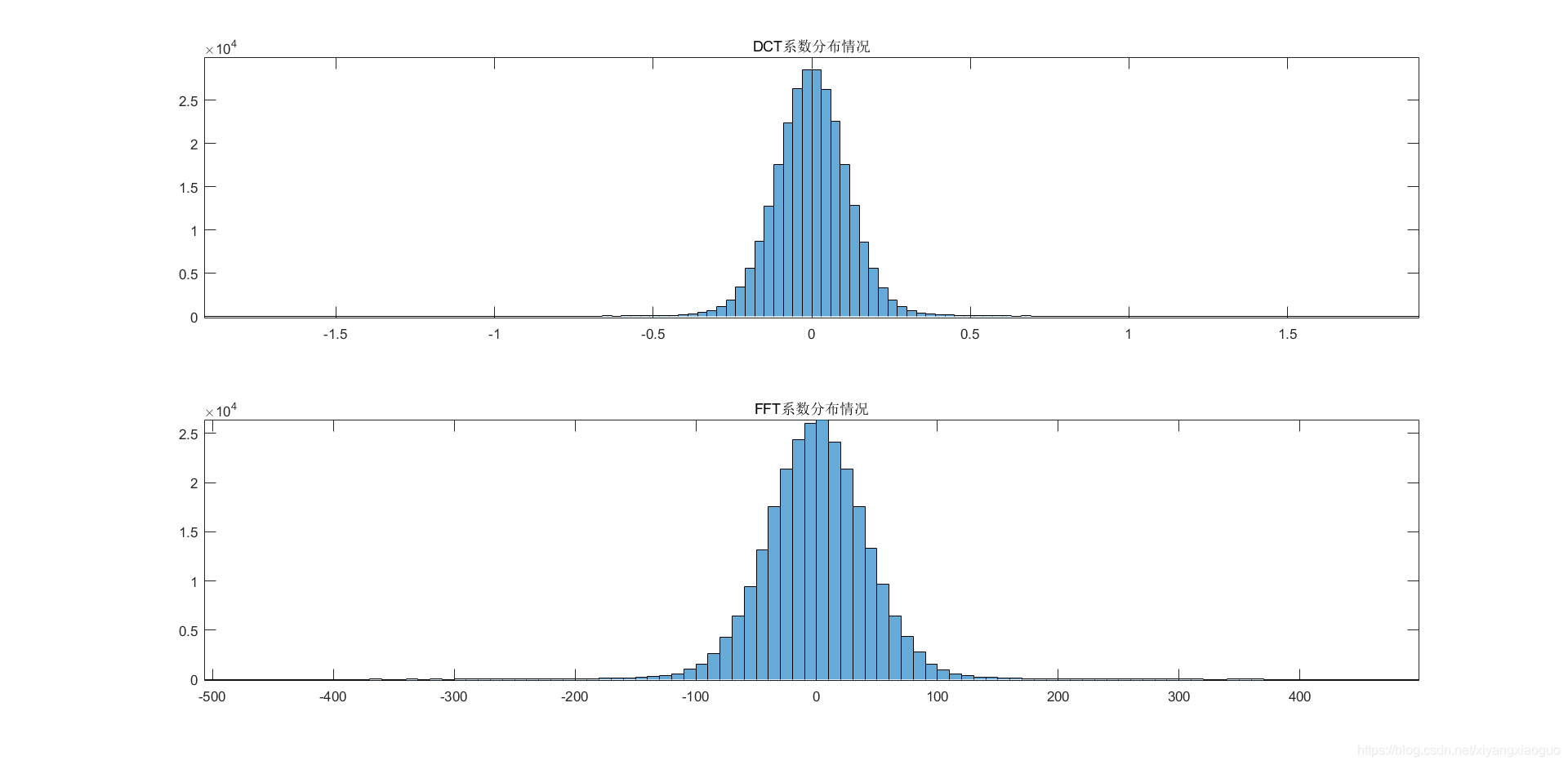
对于同一个图像，进行dct2和fft2两种变换时，考察其变换后系数分布。dct2变换后的系数为实数，fft2变换后的系数为复数，复数取实部进行对比：

dct2变换的系数基本分布在-1到1之间；而fft2变换的系数则分布在-300到300之间，二值的值差异很大（300倍的差异）

对于图像中的块与块之间，其系数的差异可以通过距离刻画

clear;
woman=imread('C:\Users\ThinkPad\Pictures\lena.jpg');

X=mat2gray(woman);

noise=randn(size(X));

sigma=0.1;
X=X+noise*sigma;

%进行dct2变换
DCT=dct2(X);

%进行fft变换
FFT=fft2(X);


figure
subplot(2,1,1)
%查看DCT系数分布情况
histogram(DCT);
title('DCT系数分布情况');

subplot(2,1,2)
%查看FFT系数分布情况
histogram(real(FFT));
title('FFT系数分布情况');

%取图像中的block，对比block与block之间的系数差异分布
%block取8*8大小，系数差异用距离d=sum((block1-block2).^2)刻画

distanceDCT=zeros(250000,1);
distanceFFT=zeros(250000,1);
nd=1;
bsz=8;
DCTref_block(:,:)=DCT(100:100+bsz-1,100:100+bsz-1); %在图像中找一个block作为参考，其他的block与之求差异
FFTref_block(:,:)=FFT(100:100+bsz-1,100:100+bsz-1);
for i=1:size(X,1)-bsz
    for j=1:size(X,2)-bsz
        
        %dct2
        tran_block(:,:)=DCT(i:i+bsz-1,j:j+bsz-1);
        dev=DCTref_block-tran_block;
        dev2=dev.*dev; %实数求平方
        distanceDCT(nd)=sum(dev2(:));
        
        
        %fft2
        tran_block(:,:)=FFT(i:i+bsz-1,j:j+bsz-1);
        dev=FFTref_block-tran_block;
        dev2=dev.*conj(dev); %复数求模方
        distanceFFT(nd)=sum(dev2(:));
        
        nd=nd+1;
    end
end

figure
subplot(2,1,1)
%查看DCT系数差异分布情况
histogram(log(distanceDCT));
title('DCT系数差异分布情况');

subplot(2,1,2)
%查看FFT系数差异分布情况
histogram(log(distanceFFT));
title('FFT系数差异分布情况');

上图的结果是对block之间的系数差异取对数之后的分布，对于DCT系数的差异，其最可机的位置在0.95处，即distance=2.58处

对于FFT系数的差异，最可机的位置在12.9，即distance=400310处，

因此，当需要设置一个阈值作为block与block相似性判断标准时，可以采用的合理的阈值：

对于DCT变换，threshold=exp(0.6)=1.82;

对于FFT变换，threshold=exp(12.6)=296560;

来源：CSDN

作者：xiyangxiaoguo

链接：https://blog.csdn.net/xiyangxiaoguo/article/details/104607237

标签

fft

matlab