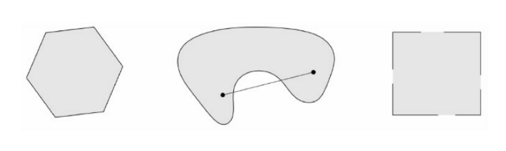
Definition 1.1 A set S is convex if, for any x,y ∈ \in ∈ θ ∈ R \theta \in \mathbb{R} θ ∈ R ≤ θ ≤ \leq \theta \leq ≤ θ ≤ θ x + ( 1 − θ ) y ∈ S .
\theta x + (1-\theta)y \in S.
θ x + ( 1 − θ ) y ∈ S . Defination 1.2 设向量{x i x_i x i λ i ≥ 0 \lambda_i \geq 0 λ i ≥ 0 ∑ i = 1 n λ i = 1 \sum\limits_{i=1}^{n}{\lambda_i} = 1 i = 1 ∑ n λ i = 1 ∑ i = 1 n λ i x i \sum\limits_{i = 1}^{n} \lambda_i x_i i = 1 ∑ n λ i x i x i x_i x i 凸组合 (凸线性组合)。
性质1: 任意两个凸集的交仍为凸集。
性质2: 凸集中任意有限多个点的凸组合仍属于这个凸集。
极点: 设S⊆ R n \subseteq \mathbb{R}^n ⊆ R n ∈ \in ∈ α x 1 + ( 1 − α ) x 2 , x 1 , x 2 ∈ S , α ∈ ( 0 , 1 ) \alpha x_1 + (1-\alpha)x_2, x_1, x_2 \in S, \alpha \in (0,1) α x 1 + ( 1 − α ) x 2 , x 1 , x 2 ∈ S , α ∈ ( 0 , 1 ) x = x 1 = x 2 x = x_1 = x_2 x = x 1 = x 2
方向: 设S⊆ R n \subseteq \mathbb{R}^n ⊆ R n ∈ R n 且 d ≠ 0 \in \mathbb{R}^n 且 d \neq 0 ∈ R n 且 d = 0 α d ∣ α ≥ 0 \alpha d | \alpha \geq 0 α d ∣ α ≥ 0 ⊂ \subset ⊂
极方向: 若S方向d不能表示成两个不同方向的正的线性组合,则称d为凸集S的极方向,即d = λ 1 d 1 + λ 2 d 2 , λ 1 > 0 , λ > 0 ⇒ d 1 = α d 2 , α > 0 d = \lambda_1 d_1 + \lambda_2 d_2, \lambda_1 >0, \lambda > 0 \Rightarrow d_1 = \alpha d_2, \alpha >0 d = λ 1 d 1 + λ 2 d 2 , λ 1 > 0 , λ > 0 ⇒ d 1 = α d 2 , α > 0
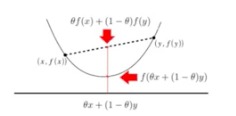
Defination 2.1 A function f : R 2 → R \mathbb{R}^2 \rightarrow \mathbb{R} R 2 → R convex if its domain (denoted D \mathcal{D} D x 1 , x 2 x_1,x_2 x 1 , x 2 ∈ D ( f ) \in \mathcal{D}(f) ∈ D ( f ) θ ∈ R , 0 ≤ θ ≤ 1 \theta \in \mathbb{R}, 0 \leq \theta \leq 1 θ ∈ R , 0 ≤ θ ≤ 1 f ( θ x 1 + ( 1 − θ ) x 2 ) ≤ θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) .
f(\theta x_1 + (1-\theta)x_2)\leq\theta f(x_1)+(1-\theta)f(x_2).
f ( θ x 1 + ( 1 − θ ) x 2 ) ≤ θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) . Defination 2.2 A function f : R 2 → R \mathbb{R}^2 \rightarrow \mathbb{R} R 2 → R concave if its domain (denoted D \mathcal{D} D x 1 , x 2 x_1,x_2 x 1 , x 2 ∈ D ( f ) \in \mathcal{D}(f) ∈ D ( f ) θ ∈ R , 0 ≤ θ ≤ 1 \theta \in \mathbb{R}, 0 \leq \theta \leq 1 θ ∈ R , 0 ≤ θ ≤ 1 f ( θ x 1 + ( 1 − θ ) x 2 ) ≥ θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) .
f(\theta x_1 + (1-\theta)x_2)\geq\theta f(x_1)+(1-\theta)f(x_2).
f ( θ x 1 + ( 1 − θ ) x 2 ) ≥ θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) .
性质1: 若f是凸集S上的凸函数(凹函数),则-f为S上的凹函数(凸函数)。
性质2: 若f1,f2时凸集S上的凸函数,α 1 , α 2 ≥ 0 \alpha_1,\alpha_2 \geq 0 α 1 , α 2 ≥ 0 α 1 f 1 + α 2 f 2 \alpha_1 f_1+\alpha_2 f_2 α 1 f 1 + α 2 f 2
性质3: 线性函数既是凸函数,也是凹函数。
凸函数的一阶充要条件为:
S为非空凸集,f为定义在S上的可微函数,则
(1)f是S上的凸函数,当且仅当f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x ) f(y) \geq f(x) + \bigtriangledown f(x)^T(y-x) f ( y ) ≥ f ( x ) + ▽ f ( x ) T ( y − x )
(2)f是S上的严格凸函数,当且仅当f ( y ) > f ( x ) + ▽ f ( x ) T ( y − x ) f(y) > f(x) + \bigtriangledown f(x)^T(y-x) f ( y ) > f ( x ) + ▽ f ( x ) T ( y − x )
图像描述:有点类似割线,切线的定义描述。示意图如下:凸函数的二阶充要条件为:
▽ 2 f ( x ) ⪰ 0 \bigtriangledown^2f(x)\succeq0 ▽ 2 f ( x ) ⪰ 0
补充:若对∀ x ∈ R n \forall x \in \mathbb{R}^n ∀ x ∈ R n ▽ 2 f ( x ) \bigtriangledown^2 f(x) ▽ 2 f ( x )
关于正定、半正定及负定,先有以下补充:
Defination 2.3 给定一个大小为 nxn 的实对称矩阵A,若对于任意长度为n的非零向量x,有x T A x > 0 x^TAx > 0 x T A x > 0 正定矩阵。
(单位矩阵是正定矩阵)
Defination 2.4 给定一个大小为 nxn 的实对称矩阵A,若对于任意长度为n的向量x,有x T A x ≥ 0 x^TAx \geq 0 x T A x ≥ 0 半正定矩阵。
(半正定矩阵包括正定矩阵,有点像非负实数和正实数的关系)
那么,如何做题如何具体判断呢?
一是求出A的所有特征值。 1)若A的特征值(|A-λ I \lambda I λ I
二是计算A的各阶主子式。 若A的各阶顺序主子式均大于零,则A是正定的;若A的各阶顺序主子式中奇数阶主子式为负,偶数阶为正,则A是负定的。注意半正定判定时需判定其所有主子式均为非负的才能说明问题,仅仅顺序主子式不可以。
霍尔维兹定理:
正定:a 11 > 0 , ∣ a 11 a 12 a 21 a 22 ∣ > 0 , ⋅ ⋅ ⋅ , ∣ a 11 ⋅ ⋅ ⋅ a 1 n ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ a n 1 ⋅ ⋅ ⋅ a n n ∣ > 0
a_{11} > 0,\begin{vmatrix}
&a_{11} &a_{12}\\
&a_{21} &a_{22}
\end{vmatrix}>0, ···, \begin{vmatrix}
a_{11} &··· &a_{1n} \\
··· &··· &··· \\
a_{n1} &··· &a_{nn}
\end{vmatrix}>0
a 1 1 > 0 , ∣ ∣ ∣ ∣ a 1 1 a 2 1 a 1 2 a 2 2 ∣ ∣ ∣ ∣ > 0 , ⋅ ⋅ ⋅ , ∣ ∣ ∣ ∣ ∣ ∣ a 1 1 ⋅ ⋅ ⋅ a n 1 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ a 1 n ⋅ ⋅ ⋅ a n n ∣ ∣ ∣ ∣ ∣ ∣ > 0
负定:( − 1 ) r ∣ a 11 ⋅ ⋅ ⋅ a 1 r ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ a r 1 ⋅ ⋅ ⋅ a r r ∣ > 0 , ( r = 1 , 2 , ⋅ ⋅ ⋅ , n )
(-1)^r\begin{vmatrix}a_{11} &··· &a_{1r}\\··· &··· &···\\a_{r1} &··· &a_{rr}\end{vmatrix}>0,(r = 1,2,···,n)
( − 1 ) r ∣ ∣ ∣ ∣ ∣ ∣ a 1 1 ⋅ ⋅ ⋅ a r 1 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ a 1 r ⋅ ⋅ ⋅ a r r ∣ ∣ ∣ ∣ ∣ ∣ > 0 , ( r = 1 , 2 , ⋅ ⋅ ⋅ , n )
Definition 3.1 Armed with the definitions of convex functions and sets, we are now equipped to consider convex optimization problems , Formally, a convex optimization problem is an optimization problem of the formm i n i m i z e f ( x ) s u b j e c t t o x ∈ C
minimize \quad f(x)\\subject\: to \quad x\in C
m i n i m i z e f ( x ) s u b j e c t t o x ∈ C m i n i m i z e f ( x ) s u b j e c t t o g i ( x ) ≤ 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k h j ( x ) = 0 , j = 1 , 2 , ⋅ ⋅ ⋅ , l
\begin{aligned}minimize\quad &f(x)\\subject\: to \quad &g_i(x)\leq0, i=1,2,···,k\\&h_j(x) = 0, j=1,2,···,l\end{aligned}
m i n i m i z e s u b j e c t t o f ( x ) g i ( x ) ≤ 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k h j ( x ) = 0 , j = 1 , 2 , ⋅ ⋅ ⋅ , l g i g_i g i h j h_j h j
定义说明:
Theorem: 凸优化问题的局部最优解是全局最优解。(可用反证法proof)
考虑以下无约束优化条件:m i n x ∈ R n f ( x ) (P1)
\begin{gathered}\underset{x\in\mathbb{R^n}}{min}\,f(x)\end{gathered} \tag{P1}
x ∈ R n min f ( x ) ( P 1 )
一阶最优性条件
Theorem: f : R n → R f:\mathbb{R^n}\to\mathbb{R} f : R n → R R \mathbb{R} R x ∗ x^* x ∗ ▽ f ( x ∗ ) = 0 \bigtriangledown f(x^*)=0 ▽ f ( x ∗ ) = 0
注:该定理为最优解的必要条件,仅使用一阶信息无法判断一个点是否为最优解。
二阶最优性条件
Theorem: f f f x ∗ x^* x ∗ ▽ f ( x ∗ ) \bigtriangledown f(x^*) ▽ f ( x ∗ ) ▽ 2 f ( x ∗ ) \bigtriangledown^2f(x^*) ▽ 2 f ( x ∗ )
补充:若Hesse矩阵为正定的,则x ∗ x^* x ∗
无约束凸规划的最优性条件:
f : R n → R f:\mathbb{R^n}\to\mathbb{R} f : R n → R 是一阶连续可微凸函数, 则x ∗ x^* x ∗ ⇔ ▽ f ( x ∗ ) = 0 \Leftrightarrow \bigtriangledown f(x^*)=0 ⇔ ▽ f ( x ∗ ) = 0
下面考虑一般约束优化问题:m i n f ( x ) s . t . g i ( x ) ≥ 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k h j ( x ) = 0 , j = 1 , 2 , ⋅ ⋅ ⋅ , l (P2)
\begin{aligned}min\quad &f(x)\\s.t.\quad &g_i(x)\geq0, i=1,2,···,k\\&h_j(x) = 0, j=1,2,···,l\end{aligned}\tag{P2}
m i n s . t . f ( x ) g i ( x ) ≥ 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k h j ( x ) = 0 , j = 1 , 2 , ⋅ ⋅ ⋅ , l ( P 2 ) f : R n → R , g i : R n → R ( i = 1 , 2 , ⋅ ⋅ ⋅ , k ) , h j : R → R ( j = 1 , 2 , ⋅ ⋅ ⋅ , l ) f:\mathbb{R^n}\to\mathbb{R},g_i:\mathbb{R^n}\to\mathbb{R}(i=1,2,···,k),h_j:\mathbb{R}\to\mathbb{R}(j=1,2,···,l) f : R n → R , g i : R n → R ( i = 1 , 2 , ⋅ ⋅ ⋅ , k ) , h j : R → R ( j = 1 , 2 , ⋅ ⋅ ⋅ , l ) Ω = { x ∈ R ∣ g i ( x ) ≥ 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k ; h j ( x ) = 0 , j = 1 , 2 , ⋅ ⋅ ⋅ , l }
\Omega=\{x\in\mathbb{R}|g_i(x)\geq0,i=1,2,···,k;h_j(x)=0,j=1,2,···,l \}
Ω = { x ∈ R ∣ g i ( x ) ≥ 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k ; h j ( x ) = 0 , j = 1 , 2 , ⋅ ⋅ ⋅ , l } x ∗ x^* x ∗
(1)有效约束 (紧约束,积极约束)g i ( x ∗ ) = 0 g_i(x^*)=0 g i ( x ∗ ) = 0
(2)非有效约束 (松约束,非积极约束)g i ( x ) > 0 g_i(x)>0 g i ( x ) > 0
有效约束指标集:I ( x ∗ ) = { i ∣ g i ( x ∗ ) = 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k }
I(x^*)=\{i|g_i(x^*)=0,i=1,2,···,k\}
I ( x ∗ ) = { i ∣ g i ( x ∗ ) = 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k } A ( x ∗ ) = I ( x ∗ ) ∪ { j = 1 , 2 , ⋅ ⋅ ⋅ , l }
A(x^*)=I(x^*)\cup\{j=1,2,···,l\}
A ( x ∗ ) = I ( x ∗ ) ∪ { j = 1 , 2 , ⋅ ⋅ ⋅ , l } KKT(Karush-Kuhn-Tucker)条件:
一般的,若f , g i , h j f,g_i,h_j f , g i , h j x ∗ x^* x ∗ x ∗ x^* x ∗ λ 1 ∗ , λ 2 ∗ , ⋅ ⋅ ⋅ , λ k ∗ , μ 1 ∗ , μ 2 ∗ , ⋅ ⋅ ⋅ , μ l ∗ \lambda_1^*, \lambda_2^*, ···, \lambda_k^*, \mu_1^*, \mu_2^*, ···, \mu_l^* λ 1 ∗ , λ 2 ∗ , ⋅ ⋅ ⋅ , λ k ∗ , μ 1 ∗ , μ 2 ∗ , ⋅ ⋅ ⋅ , μ l ∗ { ▽ f ( x ∗ ) = ∑ i = 1 k λ i ∗ ▽ g i ( x ) + ∑ j = 1 l μ j ∗ ▽ h j ( x ∗ ) 一 阶 条 件 g i ( x ∗ ) ≥ 0 , h j ( x ∗ ) = 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k ; j = 1 , 2 , ⋅ ⋅ ⋅ , l 可 行 性 条 件 λ i ∗ ≥ 0 , λ i ∗ g i ( x ∗ ) = 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k 互 补 性 条 件
\begin{cases}\bigtriangledown f(x^*) = \sum\limits_{i=1}^{k}\lambda_i^*\triangledown g_i(x)+\sum\limits_{j=1}^{l}\mu_j^*\triangledown h_j(x^*)\quad &一阶条件\\g_i(x^*)\geq0,h_j(x^*)=0,i=1,2,···,k;j=1,2,···,l\quad &可行性条件\\\lambda_i^*\geq0, \lambda_i^*g_i(x^*)=0,i=1,2,···,k &互补性条件\end{cases}
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ ▽ f ( x ∗ ) = i = 1 ∑ k λ i ∗ ▽ g i ( x ) + j = 1 ∑ l μ j ∗ ▽ h j ( x ∗ ) g i ( x ∗ ) ≥ 0 , h j ( x ∗ ) = 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k ; j = 1 , 2 , ⋅ ⋅ ⋅ , l λ i ∗ ≥ 0 , λ i ∗ g i ( x ∗ ) = 0 , i = 1 , 2 , ⋅ ⋅ ⋅ , k 一 阶 条 件 可 行 性 条 件 互 补 性 条 件
令λ ∗ = ( λ i ∗ ) , i = 1 , 2 , ⋅ ⋅ ⋅ , k , \lambda^*=(\lambda_i^*), i=1,2,···, k, λ ∗ = ( λ i ∗ ) , i = 1 , 2 , ⋅ ⋅ ⋅ , k , λ ∗ ∈ R k , μ ∗ = ( μ j ∗ ) , j = 1 , 2 , ⋅ ⋅ ⋅ , l , μ ∗ ∈ R l \lambda^* \in \mathbb{R^k}, \mu^* = (\mu_j^*), j=1,2,···, l, \mu^* \in \mathbb{R^l} λ ∗ ∈ R k , μ ∗ = ( μ j ∗ ) , j = 1 , 2 , ⋅ ⋅ ⋅ , l , μ ∗ ∈ R l ( x ∗ , λ ∗ , μ ∗ ) (x^*,\lambda^*,\mu^*) ( x ∗ , λ ∗ , μ ∗ ) x ∗ x^* x ∗
Lagrange函数: L ( x , λ , μ ) = f ( x ) − ∑ i = 1 k λ i g i ( x ) − ∑ j = 1 l μ j h j ( x )
L(x,\lambda,\mu) = f(x)-\sum\limits_{i=1}^k\lambda_ig_i(x)-\sum\limits_{j=1}^l\mu_jh_j(x)
L ( x , λ , μ ) = f ( x ) − i = 1 ∑ k λ i g i ( x ) − j = 1 ∑ l μ j h j ( x ) λ = ( λ 1 , λ 2 , ⋅ ⋅ ⋅ , λ k ) T , μ = ( μ 1 , μ 2 , ⋅ ⋅ ⋅ , μ l ) T \lambda = (\lambda_1,\lambda_2,···, \lambda_k)^T, \mu = (\mu_1,\mu_2,···,\mu_l)^T λ = ( λ 1 , λ 2 , ⋅ ⋅ ⋅ , λ k ) T , μ = ( μ 1 , μ 2 , ⋅ ⋅ ⋅ , μ l ) T
[1] Kolter Z. Convex optimization overview[J]. Convex Optimization Overview, 2008.https://funglee.github.io/ml/math/3_ConvexOpt.pdf https://blog.csdn.net/chlele0105/article/details/12238839 https://zhuanlan.zhihu.com/p/62589178
But the fruit of the Spirit is love, joy, peace, forbearance, kindness, goodness, faithfulness, gentleness and self-control.