数据分析数据挖掘（一）

相信小伙伴已经会基本的数据处理了和可视化的问题了。我们现在要进行数据挖掘的学习了。
一、数据的类型：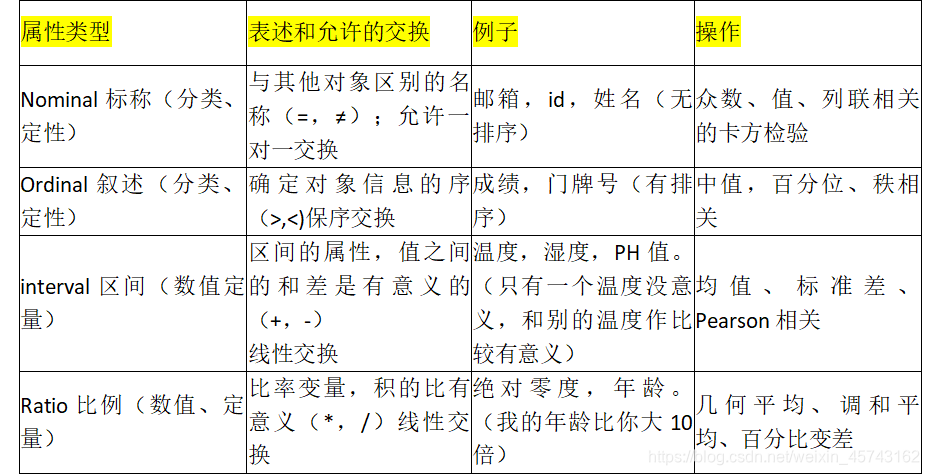
属性类型表述和允许的交换例子操作

模型：变量与变量之间的关系。
数据分析：根据变量类型和以顶的假设，来确定变量与变量之间的关系。

所有的模型都是错的，但有些是有用的。

二、数据分析和数据挖掘的关系：
1.数据的用途：记录、解释（理解）、预测、控制
2.数据分析：统计、相关、回归；已知模型下的参数估计
3.数据挖掘：发现知识；分类、聚类、回归
4.数据-信息-知识

三、概率
相信盼盼都会一些基础了，不会的话我可以再补充些更基础了。
1.条件概率：P(A|B)=P(AB)/P(B),从而可以知道若P(A)和P(B)都大于0则P(AB)=P(B)P(A|B)=P(A)P(B|A)。

2.全概率公式：设A1,A2…An是一个独立同分布的事件组，并且全部概率大于0，则对于B有,P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)…+P(An)P(B|An),这个为全概率公式。

例子：一个学校的男女(C1,C2)比例是1：1，现在从A班取出一个男生的概率是0.2，B班是0.5.
一个人是男生的概率是：P(D)=P(A)P(C1|A)+P(B)P(C1|B)=0.35
这个人如果是男生那么他可能来自A班也可能是B班，那么我们只需要算出他在A班而且他是男生的概率加上他在B班而且他是男生的概率就可以得出他是男生的概率了。

一个男生来自A班的概率是：P(A|C1)=P(C1|A)P(A)/P(D)=0.2*0.5/0.35=2/7
就是这个男生在A班而且他是男生的概率比上所有的情况（在A班而且他是男生的概率+在B班而且他是男生的概率）就是这个男生是A班的男生的概率。

4.独立试验模型:
若P(AB)=P(A)P(B)则A,B相互独立。
A,B独立的充分必要条件：P(A|B)=P(A)或P(B|A)=P(B)

5.独立实验：如果n次实验相互独立。每次实验只有两种可能结果（发生或者不发生），每次结果事件A发生的概率都相等，那么这个事件为n重贝努力模型。

6.离散型随机变量及其分布：设X为离散型随机变量，X的一切可能取值为x1,x2…X取各个可能的概率为：
pi=P{X=xi}=P(xi),i=1,2…
(1)0-1分布：即只先进行一次事件试验，该事件发生的概率为p，不发生的概率为1-p。这是一个最简单的分布.记作：X~B(1,p)
(2)二项分布：二项分布是由伯努利提出的概念，指的是重复n次独立的伯努力实验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。
公式：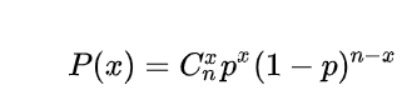
在这里插入图片描述
记作：X~B(n,p)
（3）泊松分布：泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。
公式：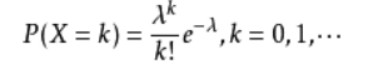

记作：X~P(λ）
7.连续型随机变量及其分布
（1）概率密度：设X为一个随机变量若存在非负可积函数,f(x)使对于任意实数x1,x2+有：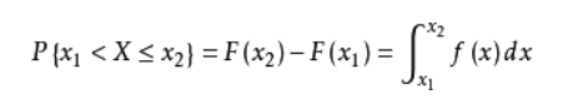
在这里插入图片描述
这就称X为连续型随机变量，f(x)为X的概率密度函数。或分布密度函数，简称概率密度（分布密度），记作X~f(x)。
ps:概率密度是概率函数的导数哦。
(2)均匀分布：如果X的概率密度为：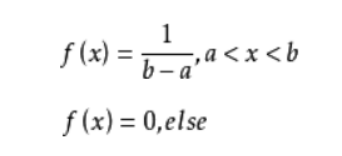

那么称X服从区间[a,b]上的均匀分布。记作：X~U(a,b)
(3)指数分布：如果X的概率密度为：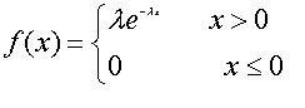
在这里插入图片描述
其中λ>0,则称X服从参数为λ的指数分布。记作X~E(λ).
(4）正态分布：如果X的概率密度为：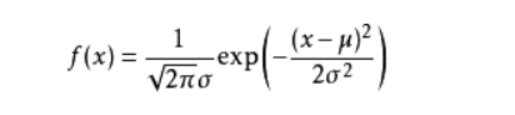

那么X为服从两个参数的正态分布，记作：X~N(μ，σ²）
当N(0,1）的时候为标准正态分布。
正态分布是概率论重最重要的一种分布。

8.随机变量的数字特征
（1）期望：
若离散型随机变量X的可能取值为xi(i=1,2…),其概率分布为P{X=xi}=pi,i=1,2…，则当x1p1+x2p2…+xipi绝对收敛时，称x1p1+x2p2…+xipi为随机变量X的数学期望。
若X为连续型的随机变量，f(x)为其密度函数，如果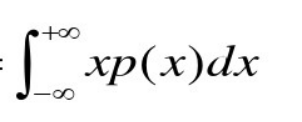
在这里插入图片描述
绝对收敛则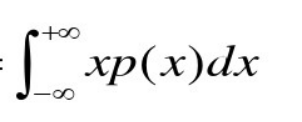

就是变量X的期望。
（2）方差：衡量随机变量取值的稳定性：
如果数学期望E（x)存在，E（X-E（X))²也存在,则称E（X-E（X))²为随机变量X的方差。
X的取值集中时方差小，分散的时候方差大。
计算公式：D（X)=E（X²)-（E(X))²
若x是离散型变量，用这个公式：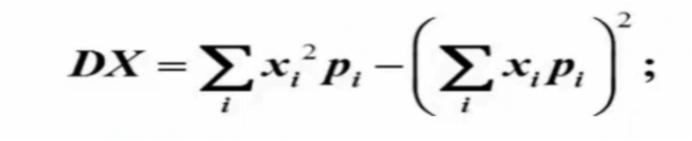
在这里插入图片描述
若x是连续型变量，用这个公式：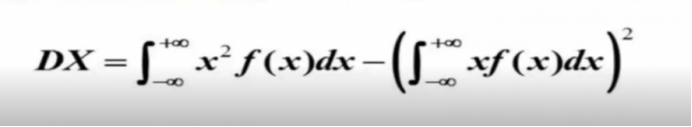

总结：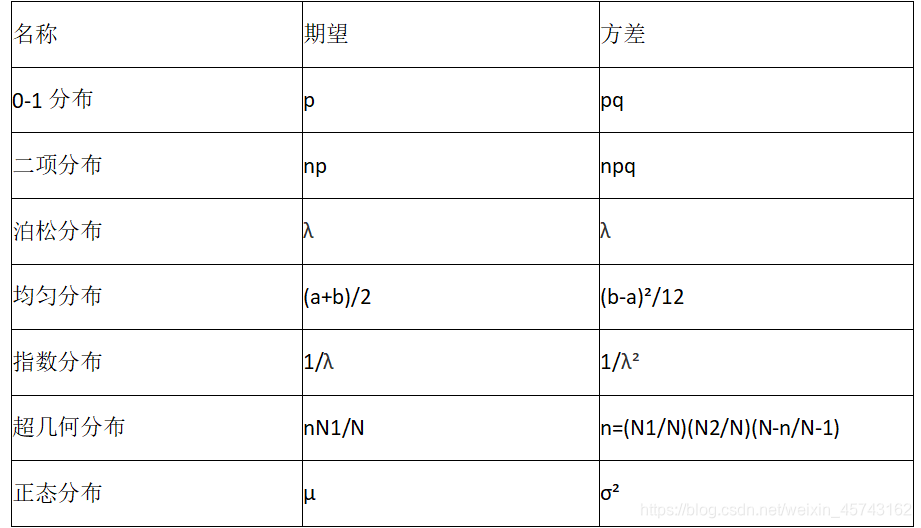

9.相关性：多个随机变量的线性关联程度的数字特征。
（1）协方差：设（X，Y)是二维随机向量，如果E[(X-EX)(Y-EY)]存在，则称之为随机向量（X，Y），记为cov(X,Y),即cov(X,Y)=：E[(X-EX)(Y-EY)]
若为离散型的：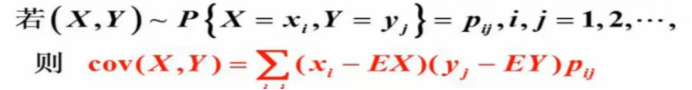
在这里插入图片描述
若为连续型的：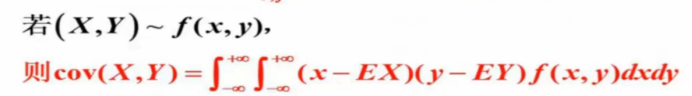

还有一个公式cov(X,Y)=E(XY)-E(X)E(Y)
（2）协方差矩阵：设（X，Y)是二维随机向量，如果协方差存在，则二阶矩阵：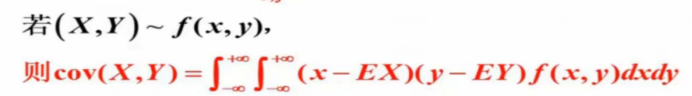

就是（X,Y）的协方差矩阵，简称协差阵。
（3）相关系数：设（X，Y)是二维随机向量，如果协方差存在，D(X),D(Y)都大于零则相关系数为，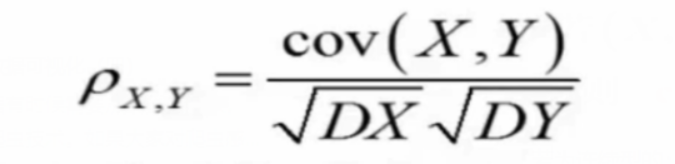
在这里插入图片描述
另一个公式：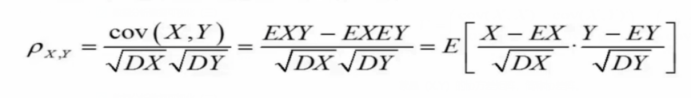

意义ρ>0时，X和Y正相关。
意义ρ<0时，X和Y负相关。
意义ρ=0时，X和Y不相关。
10.中心极限定理：在客观实际重有很多随机变量，他们有大量的独立的随机因素影响而成，每一个个别因素咋起的影响都是微小的。
在这里插入图片描述
（1）中心极限定理表明大量独立同分布的随机变量之和都近似服从正态分布。
（2）作用：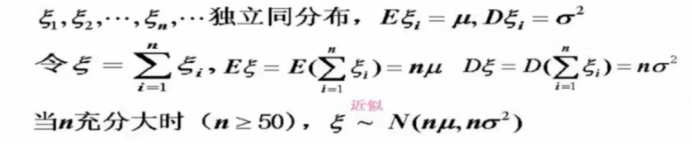

由此可近似求出由各个随机变量生成的任何事件的概率。
中心极限定理：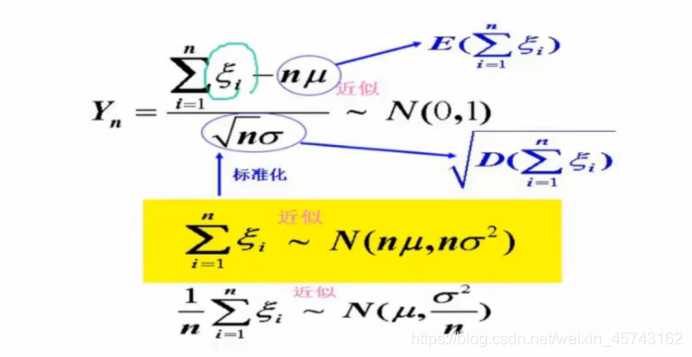

先把数据标准化。就能当作正态分布来处理。