luogu P2774 方格取数问题

有限制的问题，显然考虑全选再根据限制去掉的想法较优，我们发现一个点四周的点受限，其x或者y差一，也就是说奇偶性不同，那我们可以将其分成白点和黑点，就变成了最小割的问题，将每个白点向受限制的黑点连边，capacity为INF，每个黑点向汇点连边，capacity为该点的值，同理，源点向每个白点连边，这样受限的每一组之间都只会选出一个最小的来，通过capacity的限制来实现，最大流=最小割，将总和减去最小割(每一组最小的)就是答案

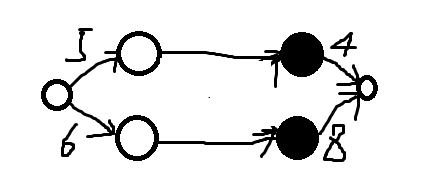每一组黑白点，capacity来限制最小权，转换求最小割

 

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) ((x)&(-x))
typedef long long LL;

const int maxm = 1e5+5;
const int INF = 0x3f3f3f3f;
const int dx[] = {1, -1, 0, 0};
const int dy[] = {0, 0, 1, -1};

struct edge{
    int u, v, cap, flow, nex;
} edges[maxm];

int head[maxm], cur[maxm], cnt, level[10005], buf[105][105], num[105][105], ID;

void init() {
    memset(head, -1, sizeof(head));
}

void add(int u, int v, int cap) {
    edges[cnt] = edge{u, v, cap, 0, head[u]};
    head[u] = cnt++;
}

void addedge(int u, int v, int cap) {
    add(u, v, cap), add(v, u, 0);
}

void bfs(int s) {
    memset(level, -1, sizeof(level));
    queue<int> q;
    level[s] = 0;
    q.push(s);
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int i = head[u]; i != -1; i = edges[i].nex) {
            edge& now = edges[i];
            if(now.cap > now.flow && level[now.v] < 0) {
                level[now.v] = level[u] + 1;
                q.push(now.v);
            }
        }
    }
}

int dfs(int u, int t, int f) {
    if(u == t) return f;
    for(int& i = cur[u]; i != -1; i = edges[i].nex) {
        edge& now = edges[i];
        if(now.cap > now.flow && level[u] < level[now.v]) {
            int d = dfs(now.v, t, min(f, now.cap - now.flow));
            if(d > 0) {
                now.flow += d;
                edges[i^1].flow -= d;
                return d;
            }

        }
    }
    return 0;
}

int dinic(int s, int t) {
    int maxflow = 0;
    for(;;) {
        bfs(s);
        if(level[t] < 0) break;
        memcpy(cur, head, sizeof(head));
        int f;
        while((f = dfs(s, t, INF)) > 0)
            maxflow += f;
    }
    return maxflow;
}

void run_case() {
    int m, n;
    LL sum = 0;
    init();
    cin >> n >> m;
    int s = 0, t = m*n+1;
    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= m; ++j) {
            cin >> buf[i][j];
            sum += buf[i][j];
            num[i][j] = ++ID;
            if((i+j)%2==1) addedge(s, ID, buf[i][j]);
            else addedge(ID, t, buf[i][j]);
        }
    }
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j) {
            if((i+j)%2==0) continue;
            for(int k = 0; k < 4; ++k) {
                int nx = i+dx[k], ny = j+dy[k];
                if(nx > n || nx < 1 || ny > m || ny < 1) continue;
                addedge(num[i][j], num[nx][ny], INF);
            }
        }
    sum -= dinic(s, t);
    cout << sum;
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0);
    run_case();
    cout.flush();
    return 0;
}

 

来源：https://www.cnblogs.com/GRedComeT/p/12298848.html