目录
本文章记录《Ray Tracing in One Weekend》笔记,代码文件请参阅 https://github.com/Intro1997/RayTracing
Chapter 1
这里我尝试使用教程中提到的 stb_image.h 去读取教程中生成的 PPM 格式图像,但是失败了。我在 stack overflow 上也提问过,截至目前(2019.12.22)仅有一人回答,且否定了成功读取的可能性。代码放在同文件夹下的 Chapter1.cpp 文件了。
Chapter 2
这里跟着作者实现了 vec3 类,也更新了之前生成图像的代码
#ifndef Vec3_h
#define Vec3_h
#include <cmath>
#include <cstdlib>
#include <iostream>
class vec3{
public:
float e[3];
vec3(){}
vec3(float e0, float e1, float e2){ e[0] = e0; e[1] = e1; e[2] = e2; }
inline float x() const { return e[0]; }
inline float y() const { return e[1]; }
inline float z() const { return e[2]; }
inline float r() const { return e[0]; }
inline float g() const { return e[1]; }
inline float b() const { return e[2]; }
inline const vec3& operator+() const { return *this; }
inline vec3 operator-() const { return vec3(-e[0], -e[1], -e[2]); }
inline float operator[](int i) const { return e[i]; }
inline float& operator[](int i) { return e[i]; }
inline vec3& operator+=(const vec3& v);
inline vec3& operator-=(const vec3& v);
inline vec3& operator*=(const vec3& v);
inline vec3& operator/=(const vec3& v);
inline vec3& operator*=(const float t);
inline vec3& operator/=(const float t);
inline float length() const {
return sqrt(e[0]*e[0] + e[1]*e[1] + e[2]*e[2]);
}
inline float square_length() const{
return e[0]*e[0] + e[1]*e[1] + e[2]*e[2];
}
inline void make_unit_vector();
friend inline std::istream & operator>>(std::istream & is, vec3 & t);
friend inline std::ostream & operator<<(std::ostream & os, vec3 & t);
friend inline vec3 operator+(const vec3 &v1, const vec3 &v2);
friend inline vec3 operator-(const vec3 &v1, const vec3 &v2);
friend inline vec3 operator*(const vec3 &v1, const vec3 &v2);
friend inline vec3 operator*(const vec3 &v1, float t);
friend inline vec3 operator*(float t, const vec3 &v1);
friend inline vec3 operator/(const vec3 &v1, const vec3 &v2);
friend inline vec3 operator/(const vec3 &v1, float t);
};
inline std::istream & operator>>(std::istream & is, vec3 & t){
is >> t.e[0] >> t.e[1] >> t.e[2];
return is;
}
inline std::ostream & operator<<(std::ostream & os, vec3 & t){
os << t.e[0] << " " << t.e[1] << " " << t.e[2];
return os;
}
inline void vec3::make_unit_vector(){
float k = 1.0 / (sqrt(e[0]*e[0] + e[1]*e[1] + e[2]*e[2]));
e[0] *= k; e[1] *= k; e[2] *= k;
}
inline vec3 operator+(const vec3 &v1, const vec3 &v2){
return vec3(v1.e[0] + v2.e[0], v1.e[1] + v2.e[1], v1.e[2] + v2.e[2]);
}
inline vec3 operator-(const vec3 &v1, const vec3 &v2){
return vec3(v1.e[0] - v2.e[0], v1.e[1] - v2.e[1], v1.e[2] - v2.e[2]);
}
inline vec3 operator*(const vec3 &v1, const vec3 &v2){
return vec3(v1.e[0] * v2.e[0], v1.e[1] * v2.e[1], v1.e[2] * v2.e[2]);
}
inline vec3 operator*(const vec3 &v1, float t){
return vec3(v1.e[0] * t, v1.e[1] * t, v1.e[2] * t);
}
inline vec3 operator*(float t, const vec3 &v1){
return vec3(v1.e[0] * t, v1.e[1] * t, v1.e[2] * t);
}
inline vec3 operator/(const vec3& v1, const vec3& v2){
return vec3(v1.e[0] / v2.e[0], v1.e[1] / v2.e[1], v1.e[2] / v2.e[2]);
}
inline vec3 operator/(const vec3& v1, float t){
return vec3(v1.e[0] / t, v1.e[1] / t, v1.e[2] / t);
}
inline float dot(const vec3 &v1, const vec3 &v2){
return v1.e[0] * v2.e[0] + v1.e[1] * v2.e[1] + v1.e[2] * v2.e[2];
}
inline vec3 cross(const vec3 &v1, const vec3 &v2){
return vec3(v1.e[1]*v2.e[2] - v1.e[2]*v2.e[1],
-(v1.e[0]*v2.e[2] - v1.e[2]*v2.e[0]),
v1.e[0]*v2.e[1] - v1.e[1]*v2.e[0]);
}
inline vec3& vec3::operator+=(const vec3& v){
e[0] += v.e[0];
e[1] += v.e[1];
e[2] += v.e[2];
return *this;
}
inline vec3& vec3::operator-=(const vec3& v){
e[0] -= v.e[0];
e[1] -= v.e[1];
e[2] -= v.e[2];
return *this;
}
inline vec3& vec3::operator*=(const vec3& v){
e[0] *= v.e[0];
e[1] *= v.e[1];
e[2] *= v.e[2];
return *this;
}
inline vec3& vec3::operator/=(const vec3& v){
e[0] /= v.e[0];
e[1] /= v.e[1];
e[2] /= v.e[2];
return *this;
}
inline vec3& vec3::operator/=(const float t){
e[0] /= t;
e[1] /= t;
e[2] /= t;
return *this;
}
inline vec3 unit_vector(vec3 v){
return v / v.length();
}
#endif
Chapter 3
本章实现了 ray 类,使用 ray 类和 vec3 类重新生成了一张蓝色渐变图。代码放在下面了。
ray 类
#ifndef Ray_H
#define Ray_H
#include "vec3.h"
class ray{
public:
vec3 A;
vec3 B;
ray(){}
ray(const vec3 &a, const vec3 &b) { A = a; B = b; }
vec3 origin() const { return A; }
vec3 direction() const { return B; }
vec3 point_at_paramter(float t) const { return A + t*B; }
};
#endif
主程序代码:
vec3 color(const ray& r){
vec3 unit_vec = unit_vector(r.direction());
float t = 0.5 * (unit_vec.y() + 1.0);
return (1-t) * vec3(1.0, 1.0, 1.0) + t * vec3(0.5, 0.7, 1.0);
}
int main() {
const char* path = "img/test.ppm";
int nx = 200 , ny = 100;
vec3 origin(0.0, 0.0, 0.0);
vec3 left_corner(-2.0, -1.0, -1.0);
vec3 horizon = vec3(4.0, 0.0, 0.0);
vec3 vertical = vec3(0.0, 2.0, 0.0);
vec3 rgb;
ofstream outFile(path);
if(outFile.fail()){
cout << "Create file writing stream failed" << endl;
}
outFile << "P3\n" << nx << " " << ny << "\n255\n";
for(int y = ny-1; y >= 0; --y){
float v = float(y) / float(ny);
for(float x = 0; x < nx; ++x){
float u = float(x) / float(nx);
ray r(origin, left_corner + u*horizon + v*vertical);
vec3 col = color(r);
rgb[0] = int(255 * col[0]);
rgb[1] = int(255 * col[1]);
rgb[2] = int(255 * col[2]);
outFile << rgb << endl;
}
}
outFile.close();
cout << "Finish\n" << endl;
return 0;
}
Chapter 4
作者在本章视野范围内渲染了一个球(仅 2d),大致步骤如下:
- 球心在 (0.0, 0.0, 0.0) 的方程为 \(x^2 + y^2 + z^2 = R^2\)
- 球心在 (cx, cy, cz) 的方程为 \((x-cx)^2 + (y-cy)^2 + (z-cz)^2 = R^2\)
- 将 \(x,y,z,cx,cy,cz\) 分别看作两个向量在坐标轴上的分量:\(p(x,y,z),\ C(xc,yc,zc)\)
- 上一章提到过 \(p(t) = A + t*B\) \(A\) 为原点向量,\(B\) 为方向向量,\(t\) 为大小,则球方程可写成 \((p(t)-C)^2 = R^2\),整理可得:\((A+t*B-C)^2-R^2=0\)
- 进一步整理可得 \(B^2*t^2 + 2(A-C)B*t + (A-C)^2 - R^2 = 0\),其中向量乘法均为点乘。
- 由于 \((p(t)-C)\) 是 \(C\) 到某个点 \(p(t)\) 的向量,因此上述方程的未知数只有 \(t\)。
- 二次函数有无根以及根的数量可以通过 \(b^2-4ac\) 求出,这里不赘述。
据此可以实现函数:
bool hit_sphere(const vec3& center, float radius, const ray& r){
vec3 oc = r.origin() - center;
float a = dot(r.direction(), r.direction());
float b = 2.0 * dot(oc, r.direction());
float c = dot(oc, oc) - radius*radius;
float discriminant = b*b - 4*a*c;
return (discriminant > 0);
}
vec3 color(const ray& r){
if(hit_sphere(vec3(0.0, 0.0, -1.0), 0.5, r))
return vec3(1.0, 0.0, 0.0);
vec3 unit_vec = unit_vector(r.direction());
float t = 0.5 * (unit_vec.y() + 1.0);
return (1-t) * vec3(1.0, 1.0, 1.0) + t * vec3(0.5, 0.7, 1.0);
}
在函数 hit_sphere() 中,若 center 为 (0.0, 0.0, 1.0),最终结果不会收到影响。这是因为 dot(oc, r.direction() 的几何意义为两向量夹角的余弦值,而 center 为 (0.0, 0.0, 1.0) 时,b 与原先的 b 正好相反,但是在 float discriminant = b*b - 4*a*c; 中,b 取了平方,因此最终结果与原先相同。作者在下一章会修改这里的 bug。
Chapter 5
本章修改了之前能看到视角后方球体的情况,修改后的代码如下:
float hit_sphere(const vec3& center, float radius, const ray& r){
vec3 oc = r.origin() - center;
float a = dot(r.direction(), r.direction());
float b = 2.0 * dot(oc, r.direction());
float c = dot(oc, oc) - radius*radius;
float discriminant = b*b - 4*a*c;
if(discriminant < 0){
return -1.0;
}
else{
return (-b - sqrt(discriminant)) / (2.0*a);
}
}
vec3 color(const ray& r){
float t = hit_sphere(vec3(0.0, 0.0, -1.0), 0.5, r);
if(t > 0.0){
vec3 N = unit_vector(r.point_at_paramter(t) - vec3(0.0, 0.0, -1.0));
return vec3(N.x()+1, N.y()+1, N.z()+1) * 0.5f;
}
vec3 unit_vec = unit_vector(r.direction());
t = 0.5 * (unit_vec.y() + 1.0);
return (1-t) * vec3(1.0, 1.0, 1.0) + t * vec3(0.5, 0.7, 1.0);
}
之前的代码规定了光线的方向为 (-2.0, -1.0, -1.0) 和一段位移的和,但总体朝向负方向,而 \(t\) 为正时,总体方向才为正,因此要求求根公式最后的结果为正。
作者接着实现了碰撞类(hitable.h),和碰撞列表类(hitablelist.h),碰撞类提供接口,供不同物体继承并实现对应的光线碰撞检测,并记录距离摄像机最近物体的距离,体现遮挡关系,记录了法向量,光线向量和参数 t。碰撞列表类 处理继承了 碰撞类 类对象与光线的碰撞检测以及遮挡关系,对应代码请在 code 文件夹中参阅。
Chapter 6
作者在本章将 camera 抽象成 camera 类,代码如下:
#ifndef camera_h
#define camera_h
#include "vec3.h"
#include "ray.h"
class camera{
public:
vec3 origin;
vec3 lower_left_corner;
vec3 horizon;
vec3 vertical;
camera(){
lower_left_corner = vec3(-2.0, -1.0, -1.0);
horizon = vec3(4.0, 0.0, 0.0);
vertical = vec3(0.0, 2.0, 0.0);
origin = vec3(0.0, 0.0, 0.0);
}
ray get_ray(float u, float v){
return ray(origin, lower_left_corner + u * horizon + v * vertical);
}
};
#endif /* camera_h */
除此之外,由于之前的球体边缘锯齿感很强,因此作者在这里做了一下抗锯齿的处理。处理方法是在一个像素范围内,做 100 次随机的,在(0, 1)范围内的偏移,将这些颜色加起来,取平均值进行抗锯齿处理。所有代码请参阅 code。
Chapter 7
我在阅读本章教程的时候,对于作者实现 diffuse 的方法有点疑惑,因此参考了这个总结,总结写的很棒。就不在这里赘述了。关于 gamma 矫正的疑问,可以参考这个哔哩哔哩韩世麟的视频,我认为对于认识 gamma 矫正的作用有着很直观的理解。作者在文中使用的 gamma 参数为 1/2,但在 LearnOpenGL.com 中,作者认为 1/2.2 能够提供更好,更真实的效果。关于 t 的范围,上述总结文章中引用的知乎回答也很好的解决了这个疑惑。整体的代码放进了 code 文件夹。这次的代码更新了计时函数。
Chapter 8
在本章,作者将前一章的 lambertian 材质抽象成一个 material 类。材质一般有两种情况,一种是 Lambertian(模糊材质),另一种是 Metal(金属材质)。前者无规律(任意的)散射光束,后者则类似于镜面反射。material 类包含一个纯虚函数 scatter 用来设定不同材质的反射情况。想象这个场景,光线击中物体,物体散射光线,追踪被散射的光线,直到没有击中物体。
仔细分析一下上述过程,光线击中物体,物体要做出散射行为,那么这个行为要根据物体本身的属性(材质)来划分,是 Lambertian 还是 Metal。被散射出去的光应该具有该物体本身的颜色(albedo)。根据这个分析,就可以确定 material 类与之前建立的类之间的关系了。
光线击中物体,这个行为被定义在 hitable 类中,由于击中之后,要判断物体的材质,因此需要定义一个记录材质的成员变量,因此作者在 hit_record 结构体中添加了 material *mat_ptr,碰撞发生时,更新这个成员变量,用来记录被光线碰撞的物体材质。这里直接使用 material 的原因后面会提到。接着根据材质需要实现相应的 scatter 方法。因此作者实现了 lambertian 和 metal 类,继承 material 类,并实现纯虚函数 scatter。由于光线撞击到物体后,需要散射,继续判断是否撞击到其他物体,因此需要递归实现,并且需要记录相应的碰撞信息,因此需要包含 hit_record 结构体。这样一来就会有矛盾。material 因为需要碰撞碰撞信息因此要包含 hit_record(在 hitable 类中),hitable 类需要包含 material 类来记录被光线碰撞的物体材质信息,实际上产生了一个环状包含结构,这个是不允许的。因此,作者在 hitable 类中,创建了一个类变量,并设置了类指针,指向对应的类,这样就解决了环状包含结构。
除了完全光滑的金属材质之外,现实中也可能会出现非完全光滑的金属,这个效果可以通过对计算好的镜面反射光线方向,做一次半径为 r 的随机方向选取,其中 r 决定模糊程度,作者限制在了 0.0 到 1.0,不过可以根据自己的喜好来调整,太大了感官上就与非金属类似了。
本章的代码依旧放进了 code 文件夹中。
Chapter 9
作者在本章对实现了电介质(玻璃,水,钻石等等)的折射效果。然而在实际情况中,对于折射率(光在真空中传播的速度与光在介质中传播速度的比值)较高的介质,在某个角度会出现镜面的情况(例如你在水中,水面与空气交界处的镜面效果)。
折射角度可以用以下公式计算(n 在这里为折射率):
\[n * sin(θ_1) = n' * sin(θ_2)\tag{1}\]
教程中的图示对代码的诠释不是清晰,具体计算方式可以用下面的步骤来理解:
对于一次发生在不同介质的折射,有入射光线 v,入射光线的单位向量 uv,法向量 n,有折射光线 r,入射角 \(θ_1\),折射角 \(θ_2\),如下图所示(上方为空气,下方为电介质):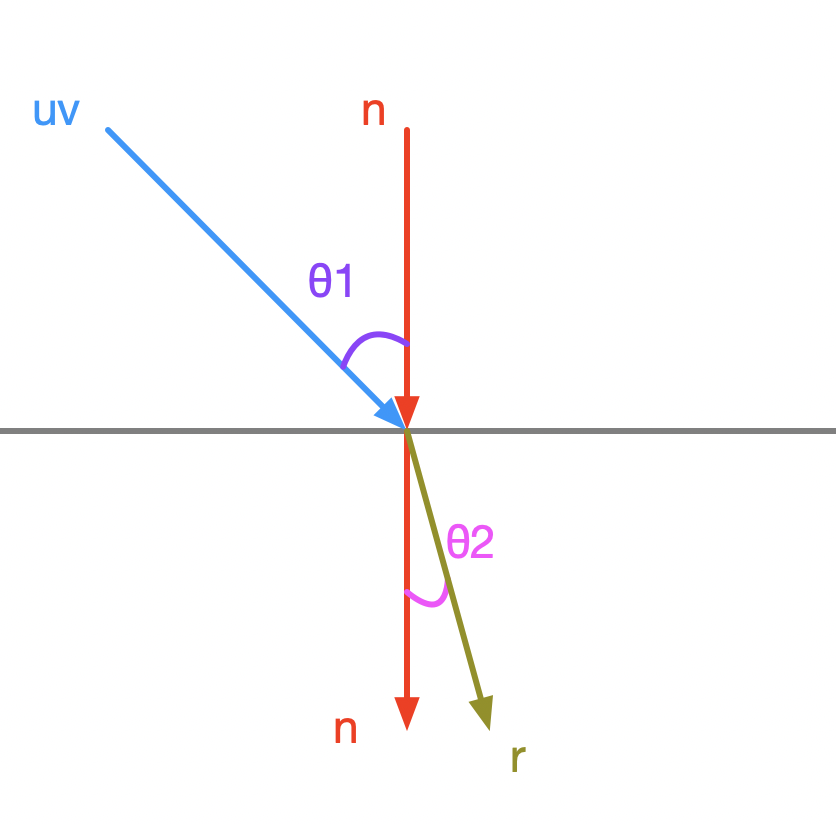
我们跟着代码一点一点分析吧。总的代码如下:
bool refract(const vec3& v, const vec3& n, float ni_over_nt, vec3& refracted) {
vec3 uv = unit_vector(v);
float dt = dot(uv, n);
float discriminant = 1.0 - ni_over_nt*ni_over_nt*(1-dt*dt);
if (discriminant > 0) {
refracted = ni_over_nt*(uv - n*dt) - n*sqrt(discriminant);
return true;
}
else
return false;
}
第二,三行就不做解释了,它是对入射向量的单位化以及计算 uv 和 法向量 n 之间角度 \(θ_1\) 的余弦值 \(cos(θ_1)\),我们从 discriminant 那一行看起
float discriminant = 1.0 - ni_over_nt*ni_over_nt*(1-dt*dt);
1-dt*dt 实际上是计算了 \(sin^2(θ_1)\),ni_over_nt 变量对应着值 \(\frac{n}{n'}\),因此 ni_over_nt*ni_over_nt*(1-dt*dt) 计算的是 \(sin^2(θ_2)\),那么 discriminant 就表示 \(cos^2(θ_2)\)。上式小于 0 的不等式为:
\[\frac{n_i}{n_r}^2 * sin(θ_1)^2>1\]
取 ni_over_nt = 1.5,时,\(2.25 * sin(x)^2 = y\) 部分函数图像如下(图由应用 MyGraphCalc 生成,绿色直线表示 y=1):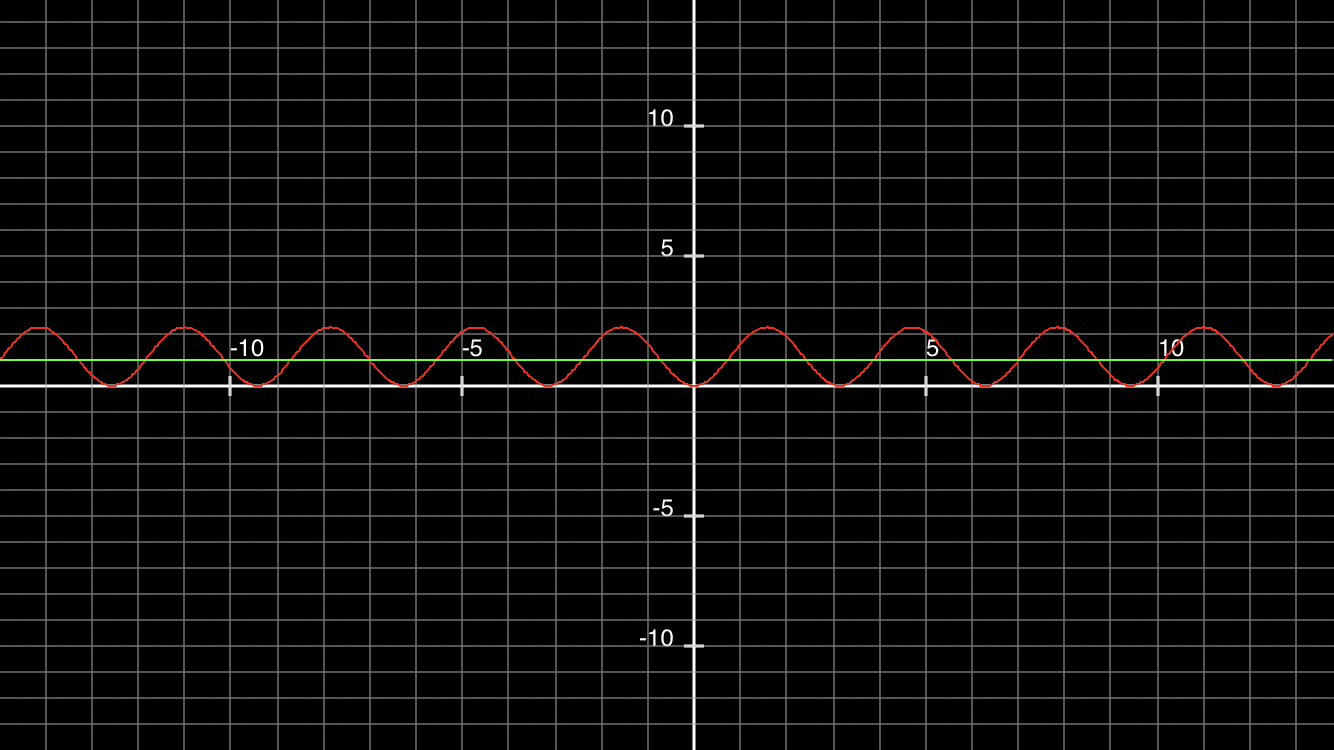
由不等式可知在绿线上侧的角度是不发生折射的,这与我们在水下观察空气和水面交界处时,一定角度发生折射,一定角度发生反射的情况一致。
倘若发生折射,refracted = ni_over_nt*(uv - n*dt) - n*sqrt(discriminant); 这行代码是怎么计算出折射光线的方向呢?先看 (uv - n*dt),这个代码的含义如图所示(注意,此时 uv 与 n 的夹角大于 90°,因此 n 会改变方向):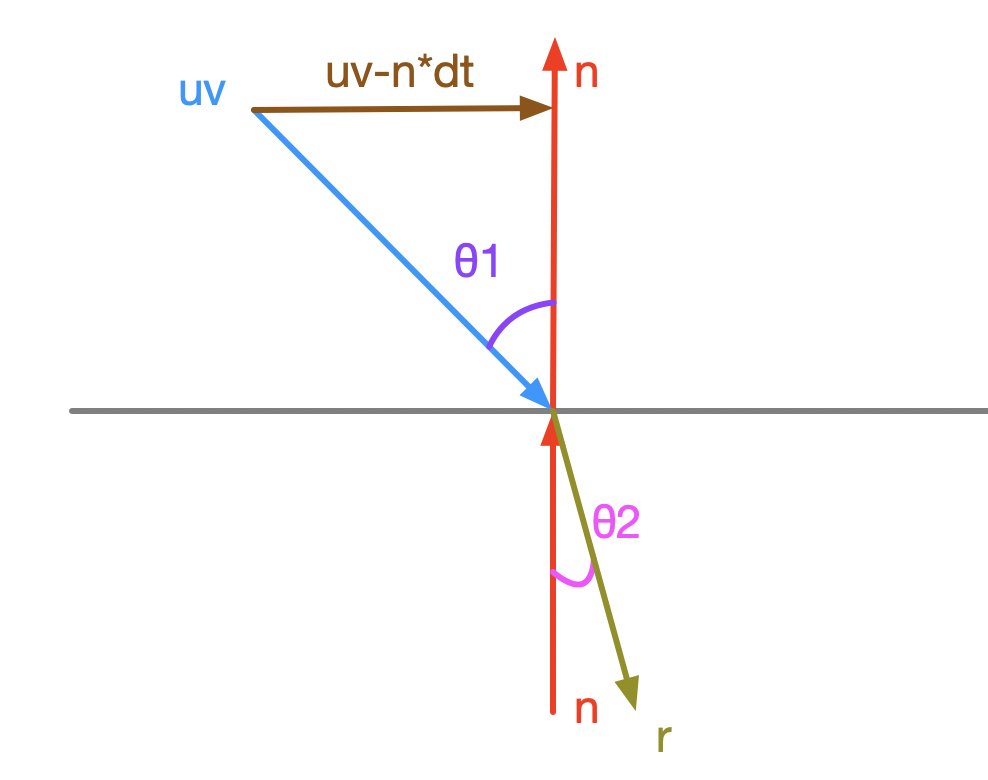
之前也说过,dt 为 \(cos(θ_1)\),因此可以看出来 (uv - n*dt) 表示的向量。我们对公式 1 进行变形,得到如下形式:
\[\frac{n}{n'} = \frac{sin(θ_2)}{sin(θ_1)}\tag{2}\] 因此 ni_over_nt*(uv - n*dt) 得出的结果如下图所示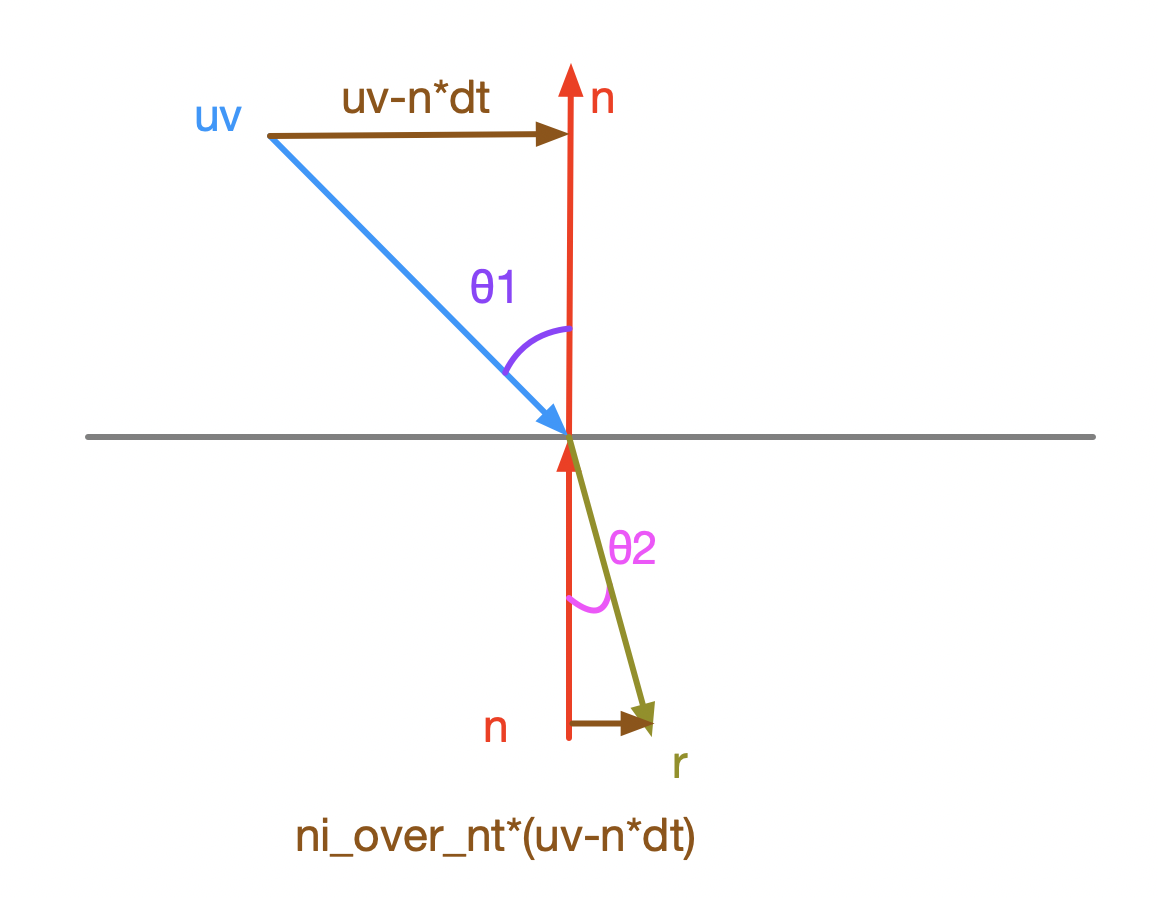
现在已经很显而易见了,最终的折射光线可以用 ni_over_nt(uv - ndt) - n*cos(θ2) 求出,这恰好与 refracted = ni_over_nt*(uv - n*dt) - n*sqrt(discriminant); 中实现的一样。
除了上方为空气,下方为电介质的情况,还需要考虑从电介质中射出到空气的情况。但是要注意,此时发现方向要取反,因为法向量方向由圆心射向空气,与入射光线(电介质内)夹角的余弦值为正,所以用上述代码无法计算出正确结果,具体的可以自己按照上面的步骤推一推。
然而上述工作只是计算了物体的折射情况,对于玻璃来说,以与法线夹角近似于 90° 的角度观察时,镜面反射会很明显。这个现象叫做 Fresnel,关于 Fresnel 现象的介绍可以参阅 Everything has Fresnel。本书的作者认为原公式非常复杂,因此使用了 Christophe Schlick 推导的多项式逼近公式。该公式的详情可以参阅 Wikipedia。我在这里简要列出该公式以及公式中涉及的参数:
\[R(θ)=R_0+(1-R_0)(cos(θ))\] \[R_0 = (\frac{n_1-n_2}{n_1+n_2})^2\] 上述公式中 θ 表示两介质交界面法向量与入射光线的夹角。关于中的 \(cosθ\),在光线从电介质出射到空气情况下,我找到了三种实现方法:
- 本书作者
cosine = ref_idx * dot(r_in.direction(), rec.normal) / r_in.direction().length();
对于代码中,公式前乘以折射率的原因还不明,原作者的 github 也有人提出这个 issue,但被作者打上了 in progress 的标签,具体请参阅这里。效果请参阅 img 文件夹下的 origin.ppm 文件,markdown 无法识别该类型图像,下同。 - 公式正确
对于公式中的描述,代码应为cosine = dot(r_in.direction(), rec.normal) / r_in.direction().length();效果参阅 img/remove.ppm - 知乎大佬
知乎大佬认为,该公式应该计算出射光线与法线夹角的余弦值,效果见 img/other.ppm,代码如下:
cosine = dot(r_in.direction(),rec.normal) / r_in.direction().length();
cosine = sqrt(1 - ref_idx*ref_idx*(1-cosine*cosine));
具体用哪个就仁者见仁智者见智了。本人就跟随教程的代码实现。
对于这里的代码:
if (drand48() < reflect_prob) {
vec3 reflected = reflect(r_in.direction(), rec.normal);
scattered = ray(rec.p, reflected);
}
取随机数可能是为了使一半的光线折射,一半的光线反射,这里不是很清楚,可以参考这个文章的解读
代码放在 code 文件夹里面了。对于电介质的 scatter 函数,当返回 false 时,计算反射光是没有意义的,因为在 color 函数中,若 scatter 返回 false,color 函数直接返回黑色。作者这里故意留下这个 bug 是为了说明人类挺难发现这个 bug(- -!)
Chapter 10
作者在这一章构建了一个可以移动视角(摄像机位置,摄像机看向的方向,摄像机视角以及视角比例可改变)的摄像机类。
在之前的章节,我们的摄像机一直处于下图的状态: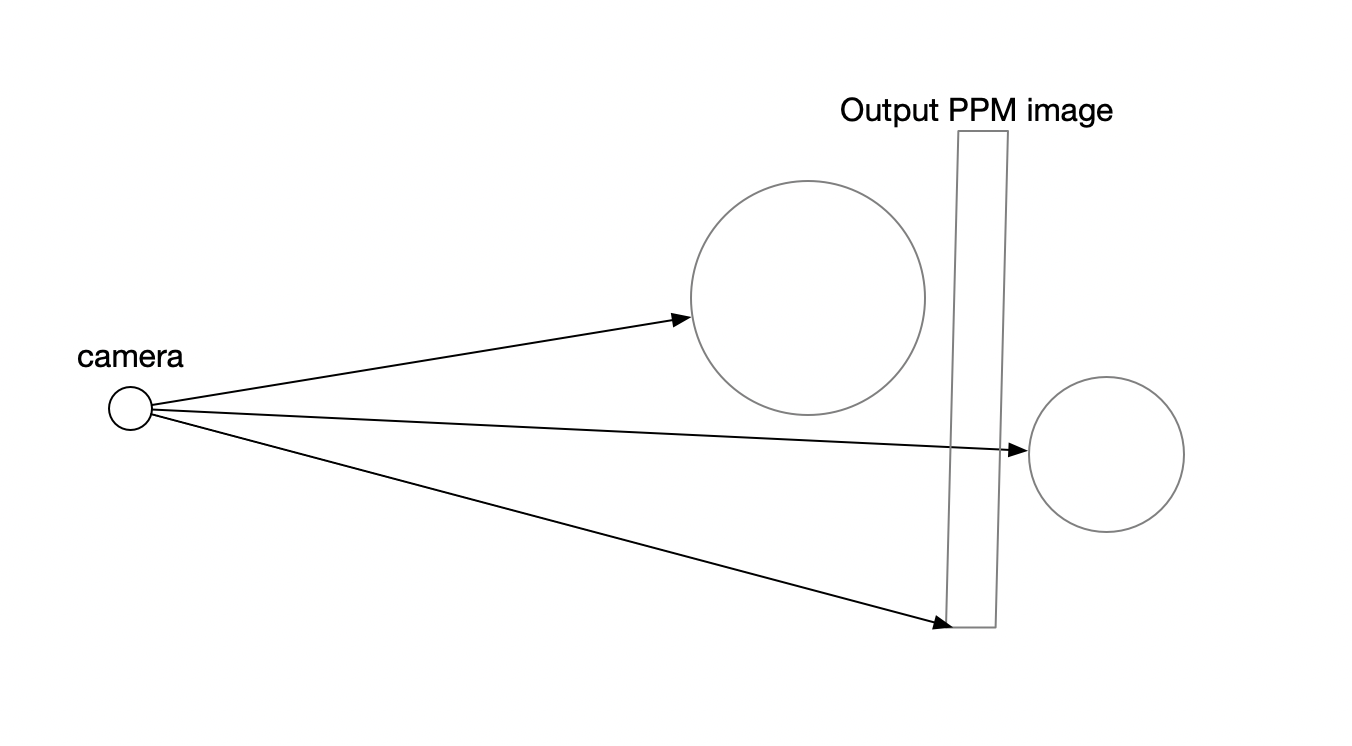
摄像机从右下角一个像素一个像素地将追踪情况写入 ppm 文件中。对于摄像机和输出平面(output ppm image)来说,它们应该是摄像机处于输出平面中心位置(x,y 轴),距离输出平面 z 距离。因此,如果想要移动摄像机,就必须移动平面,使其与摄像机的位置保持上述关系。作者将摄像机看向的方向设置为 lookat,摄像机位置为 lookfrom,前两者的与视角的关系如下图所示: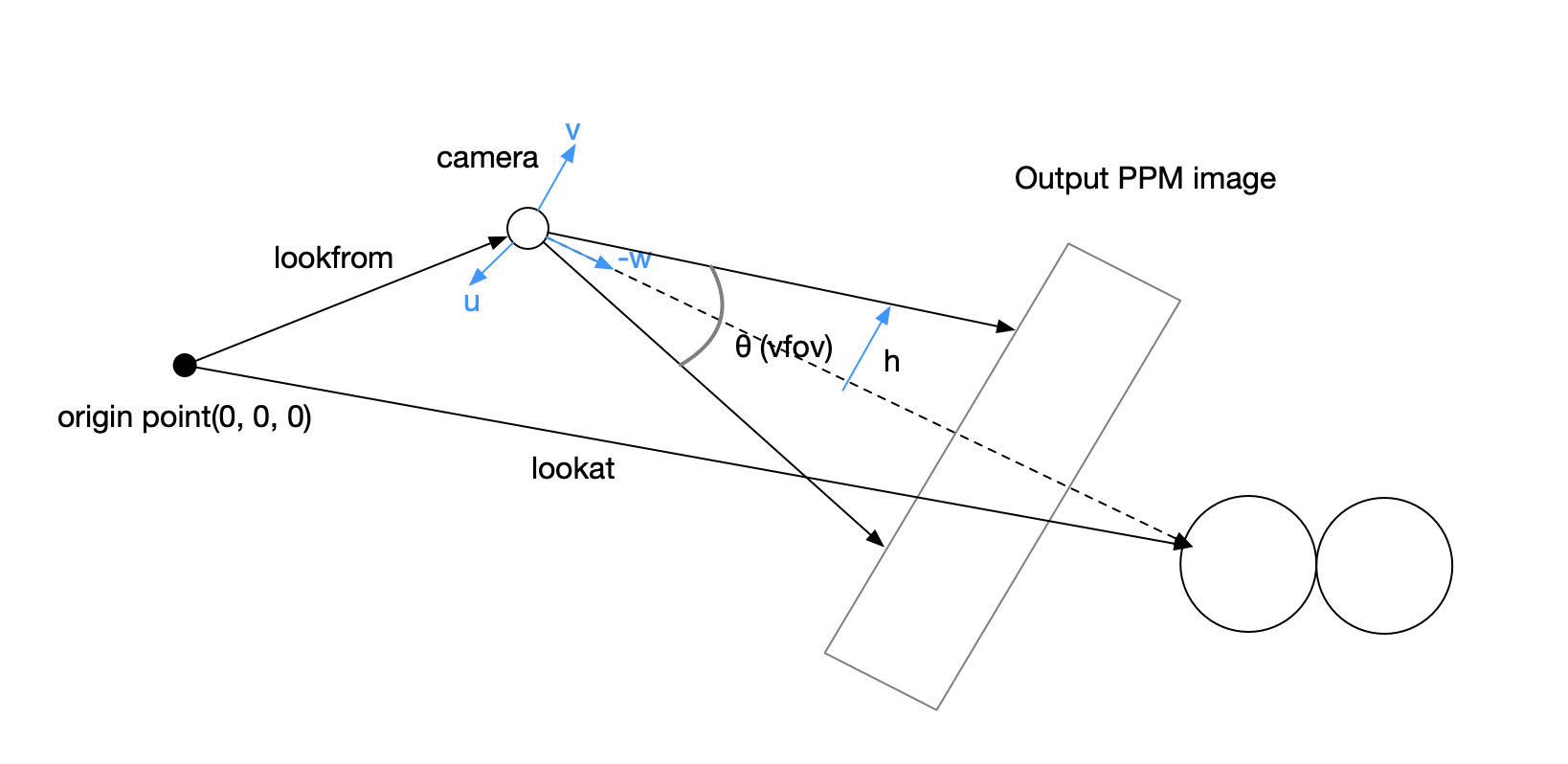
图中的 u,v,-w 可以看做一个坐标系,-w 的选取是为了使其符合右手坐标系。我们所要做的就是先构建坐标系,然后将原先的光线全部转换到当前坐标系下,由于构建过程并不复杂,这里就不赘述了,具体请参阅原文中的源代码。
Chapter 11
本章的内容我看的有点迷糊,所以结合了几篇博客去看,引用博客如下:
- https://www.jianshu.com/p/dc801008ee27?from=groupmessage&isappinstalled=0
- https://www.cnblogs.com/lv-anchoret/p/10223222.html
- https://www.cnblogs.com/AirGuanZ/p/6363175.html
- https://blog.csdn.net/FreeSouthS/article/details/90383966
由于胶片在这里就是我们要输出的图像,所以我们只需要模拟镜片(camera)和 聚焦平面(scene)即可。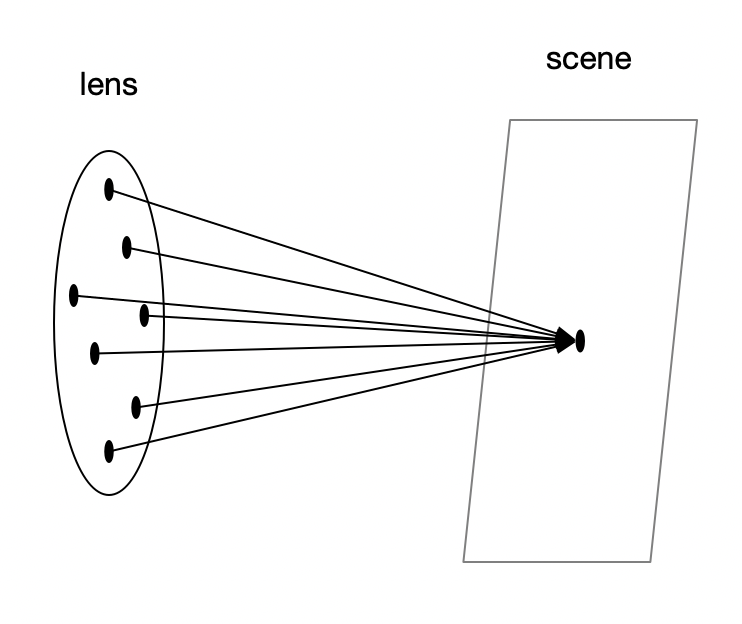
图中 lens 上的黑点为随机生成的原点,用于模拟透镜接受物体反射过来的各个方向的光线的情况。焦距为 lens 到 scene 距离 n,与 lens 距离等于 n 的物体都能被清晰的映射在输出平面上,若物体不在焦距平面,则情况如下图: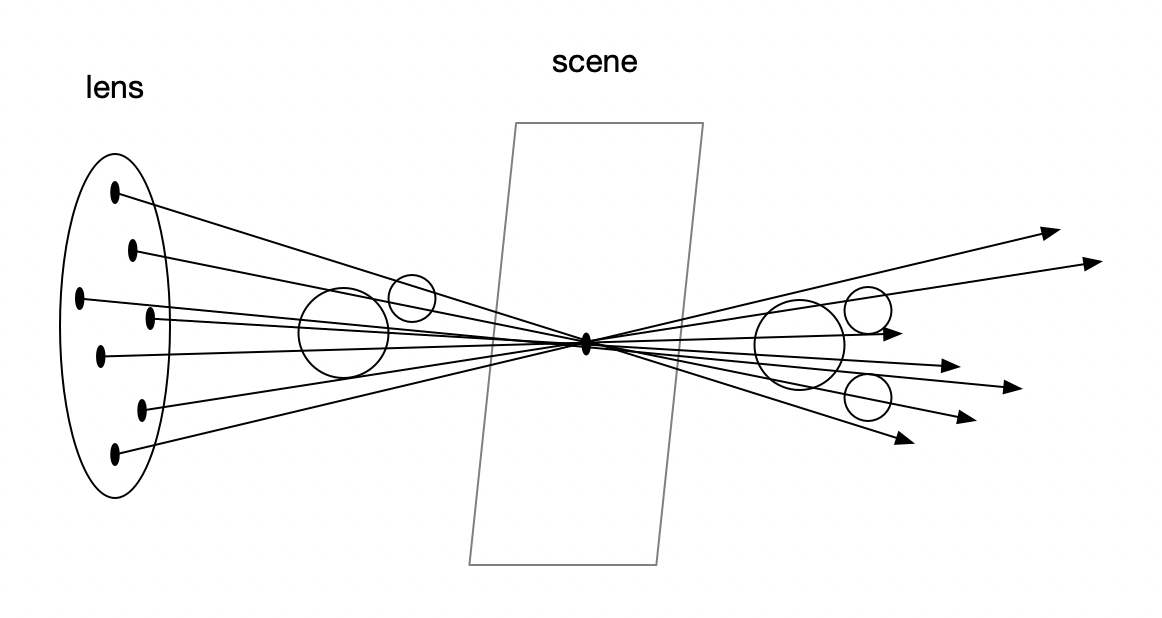
图中圆形仅代表不同球体的位置。对于相邻的像素,例如球体边缘,由于两次光线均为原先的相机位置加上一个随机偏移量,因此很难产生连续清晰的边缘,最终导致物体的模糊。同时也可以明显看出,当 lens 半径越大(光圈越大),物体会越模糊(随机偏移向量的长度范围越大)。作者代码中,用焦距与输出图像的长宽相乘,是因为之前的长宽均是在 z = 1(摄像机到成像平面的距离)的前提下,计算的 h 与 w(还记得前一章中作者在原文中提到的 half_width 和 half_height 的计算方法吗)。本章是在 z 等于焦距(lookfrom 和 lookat 间距)的前提下计算的,因此需要这样操作。
我在这里直接整合最后随机生成小球的代码,一并放在了 code 中。附上代码运行后的结果图(2000 * 1000 分辨率):
渲染共花费了 11075 秒,展示的图像是从 https://convertio.co/zh/ppm-png/ 这个网站将 ppm 文件转换为 png 文件的。
来源:https://www.cnblogs.com/Breathmint/p/12289279.html