图论——遍历算法

DFS遍历

深度优先搜索，以深度优先，直到走不下去，回退，对应的数据结构stack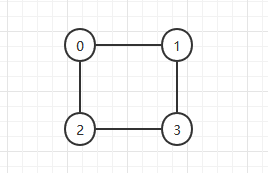
在这里插入图片描述
对于上图dfs的流程如下
第一个节点0入栈，把0标记为已访问
遍历0的所有邻接顶点，如果没有被访问就入栈，1入栈，1已访问
遍历1的所有邻接顶点，如果没有被访问就入栈，3入栈，3已访问
遍历3的所有邻接顶点，如果没有被访问就入栈，2入栈，2已访问
遍历2的所有邻接顶点，如果没有被访问就入栈，此时2的邻接顶点全部被访问，2出栈
以此类推3出栈，1出栈，0出栈，遍历完成

代码如下

public class UndirectedGraphDFS{
    private List<Integer> preOrders = new ArrayList<>();
    private List<Integer> postOrders = new ArrayList<>();
    private UndirectedGraph graph;
    private boolean[] visited;
    public UndirectedGraphDFS(UndirectedGraph graph){
        this.graph = graph;
        visited = new boolean[graph.vertexNum()];
        //可能有多个连通分量，所以得for
        for(int v=0;v<graph.vertexNum();v++){
            if(!visited[v]){
                dfs(v);
            }
        }
    }

    private void dfs(int v){
        visited[v] = true;
        preOrders.add(v);
        for(int w:graph.adj(v)) {
            if(!visited[w]){
                dfs(w);
            }
        }
        postOrders.add(v);
    }


    public Iterable<Integer> getPreOrders(){
        return preOrders;
    }
    public Iterable<Integer> getPostOrders(){
        return postOrders;
    }
    public static void main(String[] args) {
        UndirectedGraph graph = new UndirectedGraph("graph.txt");
        System.out.println(graph);
        UndirectedGraphDFS graphDFS = new UndirectedGraphDFS(graph);
        System.out.println(graphDFS.getPreOrders());
        System.out.println(graphDFS.getPostOrders());
    }
}

graph.txt

BFS遍历

广度优先遍历，以广度优先，一次性把所有的邻接节点入队，自己出队，对应数据结构queue

public class UndirectedGraphBFS {
    private UndirectedGraph graph;
    private List<Integer> orders = new ArrayList<>();
    private boolean[] visited;

    public UndirectedGraphBFS(UndirectedGraph graph){
        this.graph = graph;
        visited = new boolean[graph.vertexNum()];

        //多个联通分量必须for
        for(int v=0;v<graph.vertexNum();v++){
            if(!visited[v]){
                bfs(v);
            }
        }
    }

    public List<Integer> getOrders(){return orders;}
    private void bfs(int v){
        Queue<Integer> queue = new LinkedList();
        queue.offer(v);
        visited[v] = true;

        while(!queue.isEmpty()){
            int w = queue.poll();
            orders.add(w);
            for(int u:graph.adj(w)){
                if(!visited[u]){
                    visited[u] = true;
                    queue.offer(u);
                }
            }
        }
    }

    public static void main(String[] args) {
        UndirectedGraph graph = new UndirectedGraph("graph.txt");
        System.out.println(graph);
        UndirectedGraphBFS graphBFS = new UndirectedGraphBFS(graph);
        System.out.println(graphBFS.getOrders());
    }
}

建图类

public class UndirectedGraph {
    private int V;//顶点数
    private int E;//边数
    private TreeSet<Integer>[] adj;//邻接表，TreeSet数组存储

    public UndirectedGraph(String filename){
        File file = new File(filename);
        try(Scanner scanner = new Scanner(file)){
            V = scanner.nextInt();//顶点数
            if(V<=0) throw new RuntimeException("顶点个数必须大于0");
            adj = new TreeSet[V];
            for(int i=0;i<V;i++){
                adj[i] = new TreeSet<>();
            }
            E = scanner.nextInt();//边数
            if(E<0) throw new RuntimeException("边数不能为负数");
            for(int i=0;i<E;i++){
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);
                //自环边检测
                if(a==b){
                    throw new RuntimeException("简单图不能包含自环边");
                }
                //平行边检测
                if(adj[a].contains(b)){
                    throw new RuntimeException("简单图不能包含平行边");
                }
                adj[a].add(b);
                adj[b].add(a);
            }
        }catch (IOException e){
            e.printStackTrace();
        }
    }

    public void validateVertex(int v){
        if(v<0||v>=V){
            throw new RuntimeException("顶点下标溢出");
        }
    }
    public int vertexNum(){
        return V;
    }
    public int edgeNum(){
        return E;
    }
    public boolean hasEdge(int v,int w){
        validateVertex(v);
        validateVertex(w);
        return adj[v].contains(w);
    }

    //邻接顶点
    public Iterable<Integer> adj(int v){
        validateVertex(v);
        return adj[v];
    }

    //度
    public int degree(int v){
        validateVertex(v);
        return adj[v].size();
    }

    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        sb.append(String.format("V = %d,E = %d\n",V,E));
        for(int i=0;i<adj.length;i++){
            sb.append(i+":");
            for (Iterator<Integer> it = adj[i].iterator(); it.hasNext(); ) {
                sb.append(it.next()+" ");
            }
            sb.append("\n");
        }
        return sb.toString();
    }


    public static void main(String[] args) {
        UndirectedGraph graph = new UndirectedGraph("graph.txt");
        System.out.println(graph);
    }

来源：CSDN

作者：酒醉梦醒

链接：https://blog.csdn.net/LiuRenyou/article/details/104028762

标签

图论算法