四则运算表达式生成
软件工程大作业的结对项目–四则运算题目生成器
讲述的是前两个阶段的概要设计、详细设计、编码的内容。
整个项目的文章的链接
类的选择
有三个类,分别是存储运算符和运算数节点的二叉树类 BiTree,生成四则运算表达式的类 QuestGenerator和计算表达式结果的类solvable。QuestGenerator中的方法调用Bitree中的方法,将运算符和运算数保存在树节点中,然后生成表达式,接着调用solvable中的方法计算答案
顺序图
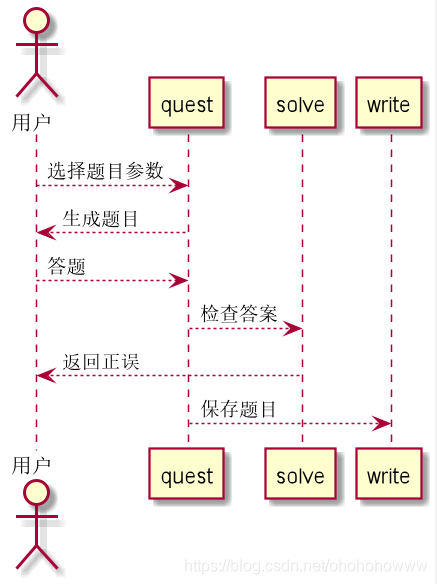
精化类的设计
BiTree类
属性部分
有lchild rchild this_level value这四个数据结构
方法部分
分别是getOperOrder获得当前符号优先级 set_lchild设置左子树 set_rchild设置右子树 to_string将表达式转换为一字符串
QuestGenerator类
属性部分
有output_list和deduplicate_set这两个数据结构
方法部分
generate方法构建一棵二叉树
其中调用了solvable类的方法solve求解表达式
deduplicate方法给表达式判重
format方法交换左右子树
change_pow方法转换乘方符号
round_up方法对结果进行四舍五入
solvable类
属性部分,是prior这个数据结构
方法部分,calculator方法转换成逆波兰表达式,调用solve方法分步求解
编码
首先生成四则运算表达式,用父节点表示符号,叶子结点表示运算符,这样构成一棵二叉树可以用来表达一个完整的四则运算表达式,通过对这棵二叉树进行中序遍历,得到中序表达式。对于表达式的运算和结果输出,进行后序遍历,转化为逆波兰表达式,方便计算机进行计算
类
表达式生成:
首先随机的生成一系列树节点,父节点是运算符,叶子节点是运算数,将生成的节点保存在存储节点的二叉树类中
接下来通过一个新类从刚才生成的节点中随机选取一个运算符和两个运算数或者两个运算符或者一个运算符一个运算数生成表达式
用到的两个类如下:
1.存储四则表达式节点的二叉树类
class BiTree:
def getOperOrder(self, ch):
if ch in ['+', '-']:
return 0
elif ch in ['*']:
return 2
elif ch in ['/']:
return 3
elif ch == '^':
return 4
def __init__(self, node_type=0, val=0):
self.node_type = node_type
self.val = val
self.lchild = None
self.rchild = None
if self.node_type == 1:
self.val = chr(self.val)
self.this_level = self.getOperOrder(self.val)
def set_lchild(self, lchild):
self.lchild = lchild
def set_rchild(self, rchild):
self.rchild = rchild
def to_string(self, upper_level=0):
if self.node_type == 1:
if upper_level > self.this_level or upper_level == self.this_level == 3 or upper_level == self.this_level \
== 4:
return '(' + self.lchild.to_string(self.this_level) + self.val + self.rchild.to_string(
self.this_level + 1) + ')'
else:
return self.lchild.to_string(self.this_level) + self.val + self.rchild.to_string(self.this_level + 1)
if int(self.val) < 0:
return '(' + str(self.val) + ')'
return str(self.val)2.生成四则运算表达式的生成类
类中定义的方法是generate deduplicate format_expression round_up change_pow_operator
generate是构建一棵二叉树
其中调用了solvable类的方法solve对生成的表达式求解
deduplicate是判断生成的表达式中是否有重复的(包括满足交换律的运算符左右子树交换后重复的情况)
format用于交换左右子树
change_pow表示是否需要更改表达式的乘方符号
round_up是对计算结果进行四舍五入
class QuestGenerator:
def __init__(self):
self.output_list = []
self.deduplicate_set = set()
def generate(self, quantity=1, operators=7, if_false=False, if_pow=False, if_fraction=False, Pow_Operator=False,
Max=9):
operands = ['+', '-', '*', '/', '^']
sum = 0
while sum < quantity:
if if_false:
nums = [BiTree(0, random.randint(-Max, Max)) for _ in range(operators + 1)]
else:
nums = [BiTree(0, random.randint(0, Max)) for _ in range(operators + 1)]
if if_pow:
ops = [BiTree(1, ord(operands[random.randint(0, 4)])) for _ in range(operators)]
else:
ops = [BiTree(1, ord(operands[random.randint(0, 3)])) for _ in range(operators)]
unfilled_ops = ops
filled_ops = nums
while len(unfilled_ops):
i = random.randint(0, len(filled_ops) - 1)
unfilled_ops[0].set_lchild(filled_ops[i])
filled_ops.pop(i)
i = random.randint(0, len(filled_ops) - 1)
unfilled_ops[0].set_rchild(filled_ops[i])
filled_ops.pop(i)
filled_ops.append(unfilled_ops[0])
unfilled_ops.pop(0)
if self.deduplicate(filled_ops[-1]):
print('Duplicated!')
continue
string = filled_ops[-1].to_string()
solve = solvable()
k = solve.Calculator(string)
if k == 'not solvable':
continue
if not if_fraction:
k = self.round_up(round(float(k.numerator / k.denominator), 3))
sum = sum + 1
string = self.changePowOp(string, Pow_Operator)
print(string, '=', str(k))
self.output_list.append(string)
self.output_list.append(str(k))
def deduplicate(self, root: BiTree):
# 深拷贝 - 避免破坏原有的随机顺序
inspect = deepcopy(root)
QuestGenerator.format_expression(inspect)
if inspect.to_string() in self.deduplicate_set:
return True
else:
self.deduplicate_set.add(inspect.to_string())
return False
def format_expression(node: BiTree):
if not node.lchild:
return
QuestGenerator.format_expression(node.lchild)
QuestGenerator.format_expression(node.rchild)
# 仅有+×可交换
if node.val in (0, 2) and node.lchild.to_string() > node.rchild.to_string():
tmp = node.lchild
node.lchild = node.rchild
node.rchild = tmp
def round_up(self, value):
return Decimal(value).quantize(Decimal('0.00'), rounding='ROUND_HALF_UP')
def changePowOp(self, string: str, Pow_Operator):
if Pow_Operator:
return string.replace('^', '**')
return string表达式运算的类:
solvable类中,Calculator是把算式转化成逆波兰表达式,其中opt列表中是运算符,data列表中是运算数。在Calculator中调用solve方法进行分步求解,solve返回当前的局部运算结果,继续参与运算。其中分数的乘方运算将分子和分母分别做乘方,然后相除。若解过大过小或除0,发现生成的这个题不可解,那么返回‘not solvable’
solvable类代码如下:
class solvable:
prior = {'+': 0, '-': 0, '*': 1, '/': 1, '^': 2, '(': -1}
def solve(self, num1: Fraction, num2: Fraction, operator):
if operator == '+':
return num1 + num2
elif operator == '-':
return num2 - num1
elif operator == '/':
if num1 == 0:
return 'not solvable'
return num2 / num1
elif operator == '*':
return num2 * num1
elif operator == '^':
k1 = num2.denominator
k2 = num2.numerator
if num1 == 0:
return Fraction(1, 1)
elif num1 >= 5 or num1 <= 0.2 or num2 >= 100 or num2 <= 0.01:
return 'not solvable'
k2 = pow(int(k2), num1)
k1 = pow(int(k1), num1)
if type(k1) == int and type(k2) == int:
return Fraction(k2, k1)
else:
return 'not solvable'
def Calculator(self, line):
opt = []
data = []
i = 0
while i < len(line):
start = i
if line[i] == '(':
if line[i + 1] == '-':
i += 1
while line[i + 1].isdigit() and i + 1 < len(line):
i += 1
data.append(Fraction(int(line[start + 1:i + 1]), 1))
i += 1
else:
opt.append(line[i])
elif line[i].isdigit():
while i + 1 < len(line) and line[i + 1].isdigit():
i += 1
data.append(Fraction(int(line[start:i + 1]), 1))
elif line[i] == ')':
while opt[-1] != '(':
k = self.solve(data.pop(), data.pop(), opt.pop())
if k == 'not solvable':
return 'not solvable'
data.append(k)
opt.pop()
else:
while opt and self.prior[line[i]] <= self.prior[opt[-1]]:
k = self.solve(data.pop(), data.pop(), opt.pop())
if k == 'not solvable':
return 'not solvable'
data.append(k)
opt.append(line[i])
i += 1
while opt:
k = self.solve(data.pop(), data.pop(), opt.pop())
if k == 'not solvable':
return 'not solvable'
data.append(k)
k = data.pop()
if k.denominator > 5000 or k.numerator > 5000:
return 'not solvable'
return kmain函数作为接口调用这些类,需要用户选择的参数有数据个数,操作符个数,算式中是否要负数,是否要乘方,是否要分数,选哪个乘方符号和最大操作数大小。
import OriginRequest as QR
def answer(quantity: int, list: list, if_fraction=0):
i = 0
correct = 0
while i < list.__len__():
if i % 2 == 0:
print(list[i], '=')
else:
if if_fraction:
st = input('answer:')
if st == list[i]:
correct += 1
else:
print('uncorrect')
else:
st = input('answer:')
st = float(st)
if st == float(list[i]):
correct = correct + 1
else:
print('uncorrect')
i = i + 1
print('correct num', correct)
print('wrong num', quantity - correct)
if __name__ == '__main__':
quantity = input('quantity:')
operators = input('operator nums:')
if_false = input('negative operands:')
if_pow = input('pow operators:')
if_fraction = input('fraction present:')
Pow_Operand = input('Pow_Operator:')
Max = input('Max nums:')
g = QR.QuestGenerator()
g.generate(quantity=int(quantity), operators=int(operators), if_false=int(if_false), if_pow=int(if_pow),
if_fraction=int(if_fraction), Pow_Operator=int(Pow_Operand), Max=int(Max))
answer(int(quantity),g.output_list,int(if_fraction))
with open('out.txt', 'w', encoding='utf-8') as f:
for out in g.output_list:
f.write(out + '\n')
程序运行结果:
单元测试
还在添加测试用例中,test.py代码如下:
import unittest
from solve import solvable
from OriginRequest import BiTree, QuestGenerator
from decimal import Decimal
from fractions import Fraction
class MyclassTest(unittest.TestCase):
def setUp(self) -> None:
self.question = QuestGenerator()
self.solution = solvable()
self.tree = BiTree()
def tearDown(self) -> None:
pass
def test_ques1(self):
ret = self.question.generate(10, 5, 0, 0, 0, 9)
print("generate questions")
print(ret)
def test_ques2(self):
ret = self.question.generate(10, 5, 1, 0, 0, 9)
print("generate questions")
print(ret)
def test_ques3(self):
ret = self.question.generate(10, 5, 0, 1, 0, 9)
print("generate questions")
print(ret)
def test_ques4(self):
ret = self.question.generate(10, 5, 0, 0, 1, 9)
print("generate questions")
print(ret)
def test_ques5(self):
ret = self.question.generate(5, 8, 0, 0, 0, 15)
print("generate questions")
print(ret)
def test_ques6(self):
ret = self.question.generate(1000, 5, 1, 1, 1, 9)
print("generate questions")
print(ret)
def test_changePowOp(self):
k = self.question.changePowOp('(5+5)^2', True)
self.assertEqual(k, '(5+5)**2', '没有转换乘方符')
print("The result of changing pow operator")
print(k)
def test_roundup1(self):
k = self.question.round_up(10.822)
self.assertEqual(k, Decimal('10.820'))
print("result of rounding up 10.822")
print(k)
def test_roundup2(self):
k = self.question.round_up(7.565)
self.assertEqual(k, Decimal('7.57'))
print("result of rounding up 7.565")
print(k)
def test_operadd(self):
k = self.tree.getOperOrder('+')
self.assertEqual(k, 0)
print("+ prior:")
print(k)
def test_opersub(self):
k = self.tree.getOperOrder('-')
self.assertEqual(k, 0)
print("- prior:")
print(k)
def test_opermul(self):
k = self.tree.getOperOrder('*')
self.assertEqual(k, 2)
print("* prior:")
print(k)
def test_operdiv(self):
k = self.tree.getOperOrder('/')
self.assertEqual(k, 3)
print("/ prior:")
print(k)
def test_operpow(self):
k = self.tree.getOperOrder('^')
self.assertEqual(k, 4)
print("^ prior:")
print(k)
def test_add1(self):
k = self.solution.solve(2, 3, '+')
self.assertEqual(k, 5)
print("result of 2 add 3:")
print(k)
def test_add2(self):
k = self.solution.solve(3 / 5, 11 / 7, '+')
self.assertEqual(k, 76 / 35)
print("result of 3/5 add 11/7:")
print(k)
def test_add3(self):
k = self.solution.solve(6.66, 99.458, '+')
self.assertEqual(k, 106.118)
print("result of 6.66 add 99.458:")
print(k)
def test_sub1(self):
k = self.solution.solve(10.87, 6.56, '-')
self.assertEqual(k, -4.31)
print("result of 6.56 sub 10.87:")
print(k)
def test_sub2(self):
k = self.solution.solve(15/7, 9/13, '-')
self.assertEqual(k, -132/91)
print("result of 9/13 - 15/7:")
print(k)
def test_mul1(self):
k = self.solution.solve(3, 4, '*')
self.assertEqual(k, 12)
print("result of 4 mul 3:")
print(k)
def test_mul2(self):
k = self.solution.solve(-3, 4, '*')
self.assertEqual(k, -12)
print("result of 4 mul -3:")
print(k)
def test_mul3(self):
k = self.solution.solve(11/3, 21/10, '*')
self.assertEqual(k, 231/30)
print("result of 21/10 mul 11/3")
print(k)
def test_mul4(self):
k = self.solution.solve(1.68, 99.135, '*')
self.assertEqual(k, 166.5468)
print("result of 99.135 mul 1.68")
print(k)
def test_div1(self):
k = self.solution.solve(4, 5, '/')
self.assertEqual(k, 1.25)
print("result of 5 div 4:")
print(k)
def test_div2(self):
k = self.solution.solve(6, 7, '/')
self.assertEqual(k, 7/6)
print("result of 7 div 6:")
print(k)
def test_div3(self):
k = self.solution.solve(1.26, 3.775, '/')
self.assertEqual(round(k, 3), 2.996)
print("result of 3.775 div 1.26:")
print(k)
def test_div4(self):
k = self.solution.solve(13/5, 7/9, '/')
self.assertEqual(k, 35/117)
print("result of 7/9 div 13/5:")
print(k)
def test_div5(self):
k = self.solution.solve(3, -4, '/')
self.assertEqual(k, -4/3)
print("result of -4 div 3:")
print(k)
def test_pow(self):
k = self.solution.solve(3, 2, '^')
self.assertEqual(k, 8)
print("result of 2 pow 3")
print(k)
if __name__ == '__main__':
suite = unittest.TestSuite()
suite.addTest(MyclassTest('test_ques1'))
suite.addTest(MyclassTest('test_ques2'))
suite.addTest(MyclassTest('test_ques3'))
suite.addTest(MyclassTest('test_ques4'))
suite.addTest(MyclassTest('test_ques5'))
suite.addTest(MyclassTest('test_ques6'))
suite.addTest(MyclassTest('test_ChangePowOp'))
suite.addTest(MyclassTest('test_roundup1'))
suite.addTest(MyclassTest('test_roundup2'))
suite.addTest(MyclassTest('test_operadd'))
suite.addTest(MyclassTest('test_opersub'))
suite.addTest(MyclassTest('test_opermul'))
suite.addTest(MyclassTest('test_operdiv'))
suite.addTest(MyclassTest('test_operpow'))
suite.addTest(MyclassTest('test_add1'))
suite.addTest(MyclassTest('test_add2'))
suite.addTest(MyclassTest('test_add3'))
suite.addTest(MyclassTest('test_sub1'))
suite.addTest(MyclassTest('test_sub2'))
suite.addTest(MyclassTest('test_mul1'))
suite.addTest(MyclassTest('test_mul2'))
suite.addTest(MyclassTest('test_mul3'))
suite.addTest(MyclassTest('test_mul4'))
suite.addTest(MyclassTest('test_div1'))
suite.addTest(MyclassTest('test_div2'))
suite.addTest(MyclassTest('test_div3'))
suite.addTest(MyclassTest('test_div4'))
suite.addTest(MyclassTest('test_div5'))
suite.addTest(MyclassTest('test_pow'))
runner = unittest.TextTestRunner()
runner.run(suite)第一个用例选择没有负数,没有乘方,没有分数表示
第二个用例加了负数
第三个用例加了乘方
第四个用例是分数表示
第五个用例改了表达式个数,运算符个数,最大的数
第六个用例生成了1000道题
test_changPowOp测changePowOp,输入以^为乘方符的表达式,看输出是不是以**为乘方符的表达式
test_roundup1和test_roundup2测round_uptest_roundup1输入了一个最后一个小数位小于5的数,看输出是否把最后一位变成0test_roundup2输入的数最后一位小数位是5,看输出是否五入了
test_operadd,test_opersub,test_opermul,test_operdiv,test_operpow测试getOperOrder返回的运算符优先级,分别输入+,-,*,/,^,查看优先级。
test_add,test_sub,test_mul,test_div,test_pow的几个测试用例分别测solve的加法,减法,乘法,除法,乘方运算
test_add1输入两个数,查看做加法后的结果
test_add2输入两个分数
test_add3输入两个小数
test_sub1输入两个小数
test_sub2输入两个分数
test_mul1输入两个整数
test_mul2输入一个正数一个负数
test_mul3是两个分数
test_mul4是两个小数
test_div1是一个大一点的数除以小一点的数
test_div2是小一点的数除以大一点的数
test_div3是两个小数
test_div4是两个分数
test_div5是一个正数一个负数
test_pow是乘方运算
测试结果如下:
来源:CSDN
作者:ohohohowww
链接:https://blog.csdn.net/ohohohowww/article/details/103995783