摘要:
作为选择排序的改进版,堆排序可以把每一趟元素的比较结果保存下来,以便我们在选择最小/大元素时对已经比较过的元素做出相应的调整。
堆排序是一种树形选择排序,在排序过程中可以把元素看成是一颗完全二叉树,每个节点都大(小)于它的两个子节点,当每个节点都大于等于它的两个子节点时,就称为大顶堆,也叫堆有序; 当每个节点都小于等于它的两个子节点时,就称为小顶堆。



(大顶堆(有序堆)) (小顶堆)
算法思想(以大顶堆为例):
1.将长度为n的待排序的数组进行堆有序化构造成一个大顶堆
2.将根节点与尾节点交换并输出此时的尾节点
3.将剩余的n -1个节点重新进行堆有序化
4.重复步骤2,步骤3直至构造成一个有序序列
假设待排序数组为[20,50,10,30,70,20,80]
构造堆
在构造有序堆时,我们开始只需要扫描一半的元素(n/2-1 ~ 0)即可,为什么?
因为(n/2-1)~0的节点才有子节点,如图1,n=8,(n/2-1) = 3 即3 2 1 0这个四个节点才有子节点


(图1:初始状态)
所以代码4~6行for循环的作用就是将3 2 1 0这四个节点从下到上,从右到左的与它自己的子节点比较并调整最终形成大顶堆,过程如下:
第一次for循环将节点3和它的子节点7 8的元素进行比较,最大者作为父节点(即元素60作为父节点)
【红色表示交换后的状态】


第二次for循环将节点2和它的子节点5 6的元素进行比较,最大者为父节点(元素80作为父节点)


第三次for循环将节点1和它的子节点3 4的元素进行比较,最大者为父节点(元素70作为父节点)
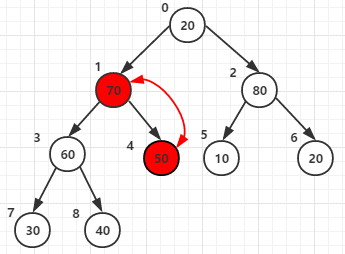

第四次for循环将节点0和它的子节点1 2的元素进行比较,最大者为父节点(元素80作为父节点)
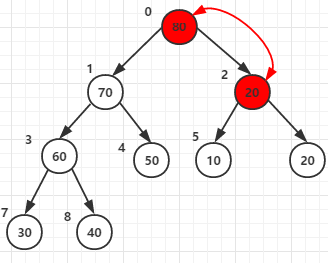

(注意这里,元素20和元素80交换后,20所在的节点还有子节点,所以还要再和它的子节点5 6的元素进行比较,这就是28行代码 i = j 的原因)
至此有序堆已经构造好了!如下图:


调整堆
下面进行while循环
(1)堆顶元素80和尾40交换后-->调整堆
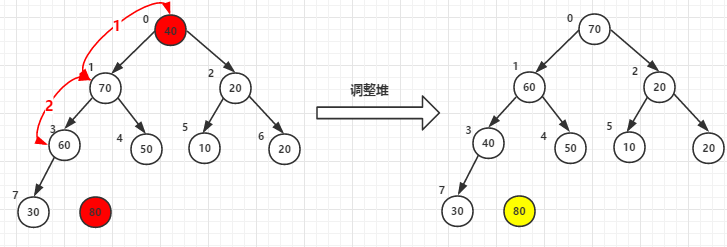

(2)堆顶元素70和尾30交换后-->调整堆
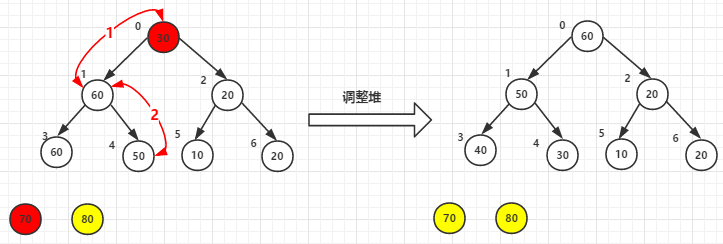

(3)堆顶元素60尾元素20交换后-->调整堆
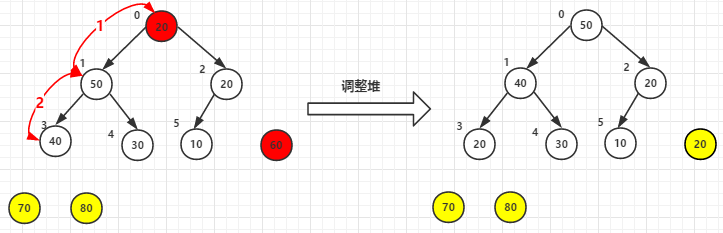

(4)其他依次类推,最终已排好序的元素如下:

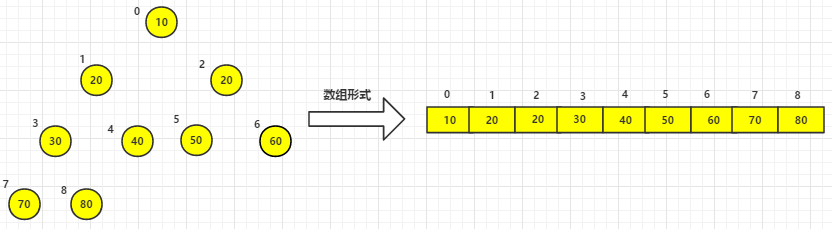
代码实现
public class HeapSort {
private static void heapSort(int[] arr) {
int len = arr.length -1;
for(int i = len/2 - 1; i >=0; i --){ //堆构造
heapAdjust(arr,i,len);
}
while (len >=0){
swap(arr,0,len--); //将堆顶元素与尾节点交换后,长度减1,尾元素最大
heapAdjust(arr,0,len); //再次对堆进行调整
}
}
public static void heapAdjust(int[] arr,int i,int len){
int left,right,j ;
while((left = 2*i+1) <= len){ //判断当前父节点有无左节点(即有无孩子节点,left为左节点)
right = left + 1; //右节点
j = left; //j"指针指向左节点"
if(j < len && arr[left] < arr[right]) //右节点大于左节点
j ++; //当前把"指针"指向右节点
if(arr[i] < arr[j]) //将父节点与孩子节点交换(如果上面if为真,则arr[j]为右节点,如果为假arr[j]则为左节点)
swap(arr,i,j);
else //说明比孩子节点都大,直接跳出循环语句
break;
i = j;
}
}
public static void swap(int[] arr,int i,int len){
int temp = arr[i];
arr[i] = arr[len];
arr[len] = temp;
}
public static void main(String[] args) {
int array[] = {20,50,20,40,70,10,80,30,60};
System.out.println("排序之前:");
for(int element : array){
System.out.print(element+" ");
}
heapSort(array);
System.out.println("\n排序之后:");
for(int element : array){
System.out.print(element+" ");
}
}
}
输出:
排序之前: 20 50 20 40 70 10 80 30 60 排序之后: 10 20 20 30 40 50 60 70 80
堆排序主要在于理解堆的构造过程和在输出最大元素后如何对堆进行重新调整,借助IDE工具的调试功能可以很好的帮助理解整个排序过程。
来源:https://www.cnblogs.com/MOBIN/p/5374217.html