Dijkstra算法原理 | 易学教程

https://blog.csdn.net/yalishadaa/article/details/55827681

算法有两个集合，集合在动态更新中。

https://www.cnblogs.com/skywang12345/p/3603935.html

学习完了原理接下来就开始代码实践吧!
**加粗样式** 邻接矩阵
邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。
假设图中顶点数为n，则邻接矩阵定义为：
在这里插入图片描述
下面通过示意图来进行解释。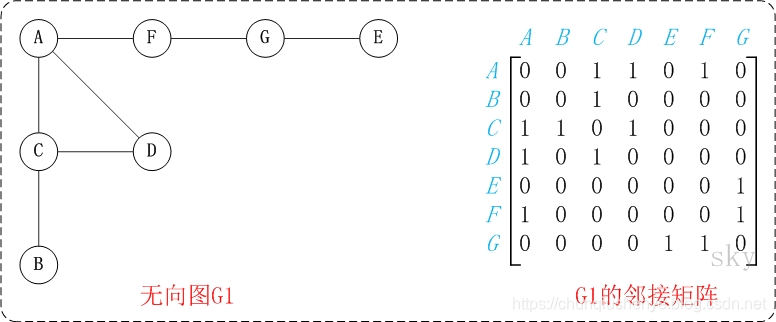

图中的G1是无向图和它对应的邻接矩阵。上面的图G1包含了"A,B,C,D,E,F,G"共7个顶点，而且包含了"(A,C),(A,D),(A,F),(B,C),(C,D),(E,G),(F,G)"共7条边。由于这是无向图，所以边(A,C)和边(C,A)是同一条边；这里列举边时，是按照字母先后顺序列举的。

上图右边的矩阵是G1在内存中的邻接矩阵示意图。A[i][j]=1表示第i个顶点与第j个顶点是邻接点，A[i][j]=0则表示它们不是邻接点；而A[i][j]表示的是第i行第j列的值；例如，A[1,2]=1，表示第1个顶点(即顶点B)和第2个顶点©是邻接点。

邻接矩阵无向图(undirected graph)的代码说明

基本定义

class MatrixUDG {
    private:
        char mVexs[MAX];         // 顶点集合
        int mVexNum;             // 顶点数
        int mEdgNum;             // 边数
        int mMatrix[MAX][MAX];   // 邻接矩阵

    public:
        // 创建图(自己输入数据),两种构造函数
        MatrixUDG();
        // 创建图(用已提供的矩阵)
        MatrixUDG(char vexs[], int vlen, char edges[][2], int elen);
        ~MatrixUDG();

        // 打印矩阵队列图
        void print();

    private:
        // 读取一个输入字符
        char readChar();
        // 返回ch在mMatrix矩阵中的位置
        int getPosition(char ch);
};

MatrixUDG是邻接矩阵对应的结构体。
mVexs用于保存顶点，mVexNum是顶点数，mEdgNum是边数；mMatrix则是用于保存矩阵信息的二维数组。
例如，mMatrix[i][j]=1，则表示"顶点i(即mVexs[i])"和"顶点j(即mVexs[j])"是邻接点；mMatrix[i][j]=0，则表示它们不是邻接点。

创建矩阵
这里介绍提供了两个创建矩阵的方法。一个是用已知数据，另一个则需要用户手动输入数据。

2.1 创建图(用已提供的矩阵)

/*
 * 创建图(用已提供的矩阵)
 *
 * 参数说明：
 *     vexs  -- 顶点数组
 *     vlen  -- 顶点数组的长度
 *     edges -- 边数组
 *     elen  -- 边数组的长度
 */
MatrixUDG::MatrixUDG(char vexs[], int vlen, char edges[][2], int elen)
{
    int i, p1, p2;

    // 初始化"顶点数"和"边数"
    mVexNum = vlen;
    mEdgNum = elen;
    // 初始化"顶点"
    for (i = 0; i < mVexNum; i++)
        mVexs[i] = vexs[i];

    // 初始化"边"
    for (i = 0; i < mEdgNum; i++)
    {
        // 读取边的起始顶点和结束顶点
        p1 = getPosition(edges[i][0]);
        p2 = getPosition(edges[i][1]);

        mMatrix[p1][p2] = 1;
        mMatrix[p2][p1] = 1;
    }
}

该函数的作用是利用已知数据来创建一个邻接矩阵无向图。实际上，在本文的测试程序源码中，该方法创建的无向图就是上面图G1。具体的调用代码如下：

char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
char edges[][2] = {
    {'A', 'C'}, 
    {'A', 'D'}, 
    {'A', 'F'}, 
    {'B', 'C'}, 
    {'C', 'D'}, 
    {'E', 'G'}, 
    {'F', 'G'}};
int vlen = sizeof(vexs)/sizeof(vexs[0]);
int elen = sizeof(edges)/sizeof(edges[0]);
MatrixUDG* pG;

pG = new MatrixUDG(vexs, vlen, edges, elen);

2.2 创建图(自己输入)

/* 
 * 创建图(自己输入数据)
 */
MatrixUDG::MatrixUDG()
{
    char c1, c2;
    int i, p1, p2;

    // 输入"顶点数"和"边数"
    cout << "input vertex number: ";
    cin >> mVexNum;
    cout << "input edge number: ";
    cin >> mEdgNum;
    if ( mVexNum < 1 || mEdgNum < 1 || (mEdgNum > (mVexNum * (mVexNum-1))))
    {
        cout << "input error: invalid parameters!" << endl;
        return ;
    }

    // 初始化"顶点"
    for (i = 0; i < mVexNum; i++)
    {
        cout << "vertex(" << i << "): ";
        mVexs[i] = readChar();
    }

    // 初始化"边"
    for (i = 0; i < mEdgNum; i++)
    {
        // 读取边的起始顶点和结束顶点
        cout << "edge(" << i << "): ";
        c1 = readChar();
        c2 = readChar();

        p1 = getPosition(c1);
        p2 = getPosition(c2);
        if (p1==-1 || p2==-1)
        {
            cout << "input error: invalid edge!" << endl;
            return ;
        }

        mMatrix[p1][p2] = 1;
        mMatrix[p2][p1] = 1;
    }
}

该函数是通过读取用户的输入，而将输入的数据转换成对应的无向图。
邻接矩阵无向图的完整源码

https://github.com/wangkuiwu/datastructs_and_algorithm/blob/master/source/graph/basic/udg/cplus/MatrixUDG.cpp

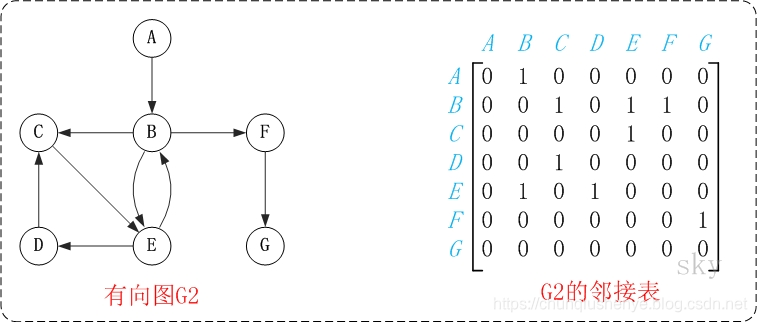
在这里插入图片描述
图中的G2是无向图和它对应的邻接矩阵。

通常采用两个数组来实现邻接矩阵：一个一维数组用来保存顶点信息，一个二维数组来用保存边的信息。
邻接矩阵的缺点就是比较耗费空间。

邻接表

邻接表是图的一种链式存储表示方法。它是改进后的"邻接矩阵"，它的缺点是不方便判断两个顶点之间是否有边，但是相对邻接矩阵来说更省空间。
在这里插入图片描述图中的G1是无向图和它对应的邻接矩阵。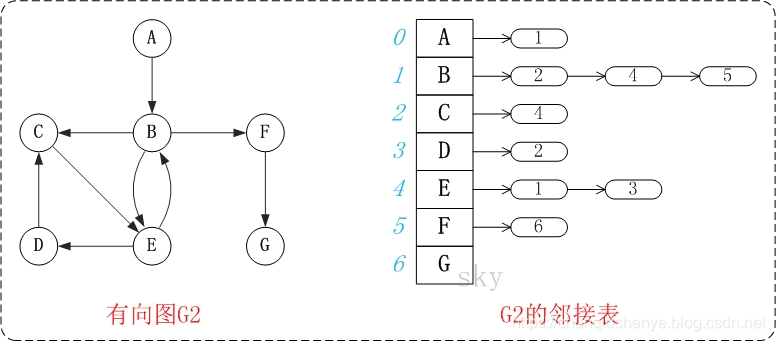

图中的G2是有向图和它对应的邻接矩阵。

来源：CSDN

作者：春秋深夜

链接：https://blog.csdn.net/qq_21950671/article/details/103888192

标签

邻接矩阵

char函数

char

dijkstra