在这里插入图片描述

ABSTRACT

网络嵌入是学习网络中顶点的低维表示的一种重要方法，旨在捕获和保留网络结构。几乎所有现有的网络嵌入方法都采用浅层模型。但是，由于底层网络结构很复杂，因此浅层模型无法捕获高度非线性的网络结构，从而导致次优网络表示形式。因此，如何找到一种能够有效捕获高度非线性网络结构并保留全局和局部结构的方法是一个悬而未决的重要问题。 为了解决这个问题，本文提出了一种结构化深度网络嵌入方法，即SDNE。更具体地说，我们首先提出一个半监督深度模型，该模型具有多层非线性函数，从而能够捕获高度非线性的网络结构。然后，我们建议联合利用一阶和二阶邻近度来保留网络结构。无监督组件使用二阶接近度来捕获全局网络结构。而一阶接近度用作受监管组件中的受监管信息，以保留本地网络结构。通过在半监督深度模型中共同优化它们，我们的方法既可以保留本地网络结构又可以保留全局网络结构，并且对于稀疏网络具有鲁棒性。根据经验，我们在五个真实世界的网络上进行实验，包括语言网络，引文网络和三个社交网络。结果表明，与基线相比，我们的方法可以更好地重构原始网络，并在多标签分类，链接预测和可视化这三个应用中获得了可观的收益。

1. INTRODUCTION

学习网络表示面临以下巨大挑战：

（1）高度非线性：如[19]所述，网络的基础结构是高度非线性的。因此，如何设计一个模型来捕获高度非线性的结构是相当困难的。
（2）保留结构：为了支持应用程序分析网络，需要网络嵌入来保留网络结构。但是，网络的底层结构非常复杂[24]。顶点的相似性取决于本地和全局网络结构。因此，如何同时保留本地和全球结构是一个难题。
（3）稀疏性：许多现实世界中的网络通常如此稀疏，以至于仅利用观察到的非常有限的链接不足以达到令人满意的性能[21]。

在过去的几十年中，已经提出了许多采用浅层模型的网络嵌入方法，例如IsoMAP [29]，拉普拉斯特征图（LE）[1]和Line [26]。然而，由于浅层模型的表示能力有限[2]，它们很难捕获高度非线性的网络结构[30]。尽管某些方法采用核技术[32]，如[36]所述，但核方法也是浅层模型，无法很好地捕获高度非线性的结构。
为了很好地捕获高度非线性的结构，在本文中，我们提出了一个新的深度模型来学习网络的顶点表示。这是由最近的深度学习成功推动的，深度学习已被证明具有强大的表示能力，可以学习复杂的数据结构[2]，并且在处理图像[15]，文本[25]和音频方面也取得了相当大的成功。 [10]个数据。特别是，在我们提出的模型中，我们设计了由多个非线性函数组成的多层体系结构。多层非线性函数的组成可以将数据映射到高度非线性的潜在空间中，从而能够适应高度非线性的网络结构。
为了解决深度模型中的结构保留和稀疏性问题，我们进一步建议在学习过程中共同利用一阶和二阶邻近性[26]。一阶接近度是仅在由边链接的顶点之间的局部成对相似性，这是局部网络结构的特征。但是，由于网络稀疏，因此缺少许多合法链接。结果，一阶邻近度不足以表示网络结构。因此，我们进一步提出了二阶接近度，它表示顶点邻域结构的相似性，以捕获全局网络结构。随着一阶和二阶的接近，我们能很好地表征局部和全局的网络结构。为了在深度模型中同时保留本地和全局网络结构，我们提出了一种半监督体系结构，其中无监督组件重构二阶邻近度以保留全局网络结构，而受监督组件则利用一阶邻近度作为监督对象的信息以保留本地网络结构。结果，学习到的表示可以很好地保留本地和全局网络结构。另外，如图1所示，具有二阶邻近度的顶点对的数量比具有一阶邻近度的顶点的数量大得多。因此，就表征网络结构而言，二阶接近度的导入能够提供更多的信息。结果，我们的方法对于稀疏网络是鲁棒的。
根据经验，我们在五个真实世界的网络数据集和四个真实世界的应用程序上进行实验。结果表明，与基准相比，我们的方法生成的表示可以更好地重构原始网络，并且可以在各种任务和各种网络（包括非常稀疏的网络）上获得可观的收益。它表明我们在高度非线性空间中学习到的表示可以很好地保留网络结构，并且对稀疏网络具有鲁棒性。
总而言之，本文的贡献如下：

我们提出了一种结构化深度网络嵌入方法，即SDNE，以执行网络嵌入。该方法能够将数据映射到高度非线性的潜在空间以保留网络结构，并且对于稀疏网络具有鲁棒性。据我们所知，我们是最早使用深度学习来学习网络表示的国家之一。
我们提出了一种具有半监督架构的新深度模型，该模型同时优化了一阶和二阶接近度。结果，学习到的表示保留了本地和全局网络结构，并且对于稀疏网络具有鲁棒性。
对五个真实数据集和四个应用场景进行了广泛评估。结果证明了该方法在多标签分类，重建，链接预测和可视化方面的优越性。具体来说，当标记的数据得到支持时，我们的方法可以比基线获得更大的改进（20％）。在某些情况下，我们只需要减少60％的训练样本，但仍然可以获得更好的性能。

2. RELATED WORK

表示学习长期以来一直是机器学习的重要问题，许多工作旨在学习样本的表示[3，35]。深度神经网络的最新进展表明，它们具有强大的表示能力[12]，并且可以为许多类型的数据生成非常有用的表示。例如，[15]提出了一个七层卷积神经网络来生成图像表示用于分类。 [33]提出了一种多模态深度模型来学习图像-文本统一表示，以实现跨模态检索任务。
然而，据我们所知，几乎没有处理网络的深度学习工作，特别是学习网络表示。在[9]中，采用了受限玻尔兹曼机来进行协同过滤。 [30]采用深度自动编码器进行图聚类。文献[5]提出了一种异构深度模型来进行异构数据嵌入。我们在两个方面与这些作品不同。首先，目标是不同的。我们的工作重点是学习可在任务之间利用的低维结构保留网络表示。其次，我们考虑顶点之间的一阶和二阶邻近性，以保留本地和全局网络结构。但是它们仅关注一阶信息。

2.1 Deep Neural Network

表示学习(Representation learning)长期以来一直是机器学习的重要问题，许多工作旨在学习样本的表示[3，35]。深度神经网络的最新进展表明，它们具有强大的表示能力[12]，并且可以为许多类型的数据生成非常有用的表示。例如，[15]提出了一个七层卷积神经网络来生成图像表示以进行分类。 [33]提出了一种多模态深度模型来学习图像-文本未统一的表示形式，以实现跨模态检索任务。
然而，据我们所知，几乎没有处理网络的深度学习工作，特别是学习网络表示。在[9]中，采用了受限玻尔兹曼机来进行协同过滤。 [30]采用深度自动编码器进行图聚类。文献[5]提出了一种异构深度模型来进行异构数据嵌入。我们在两个方面与这些作品不同。首先，目标是不同的。我们的工作重点是学习可在任务之间利用的低维结构保留网络表示。其次，我们考虑顶点之间的一阶和二阶邻近性，以保留本地和全局网络结构。但是它们仅关注一阶信息。

2.2 Network Embedding

我们的工作解决了网络嵌入的问题，该问题旨在学习网络的表示形式。一些早期的工作，例如本地线性嵌入（LLE）[22]，IsoMAP [29]，首先基于特征向量构造了亲和图( affinity graph)，然后求解了主导的特征向量作为网络表示。最近，[26]设计了两个损失函数，分别试图捕获本地和全局网络结构。此外，[4]扩展了工作以利用高阶信息。尽管这些网络嵌入方法取得了成功，但它们都采用了浅层模型。如前所述，浅层模型很难有效地捕获底层网络中的高度非线性结构。另外，尽管其中一些尝试使用一阶和高阶邻近度来保留本地和全局网络结构，但他们分别学习它们的表示形式并简单地将表示形式连接起来。显然，与在未定义的架构中同时对它们进行建模以捕获本地和全局网络结构相比，它不是最佳的。
DeepWalk [21]结合了random walk和skip-gram来学习网络表示。尽管从经验上讲是有效的，但是它缺乏明确的目标功能来阐明如何保留网络结构。倾向于仅保留二阶接近度。但是，我们的方法设计了一个明确的目标函数，该函数旨在通过保留一阶和二阶接近度来同时保留局部和全局结构。

3. STRUCTURAL DEEP NETWORK EMBEDDING

在本节中，我们首先定义问题。然后，我们介绍了建议的SDNE半监督深度模型。最后，我们对该模型进行了一些讨论和分析。

3.1 Problem Definition

我们首先给出图的定义。
定义1 （图）图表示为 $G =(V,E)$ ，其中 $V = {v_1，...，v_n}$ 表示 $n$ 个顶点， $E = \{e_{i,j}\} ^n_{i,j = 1}$ 表示边。每个边 $e_{i,j}$ 与权重 $s_{i,j}≥0$ 相关联。对于不由边链接的 $v_i$ 和 $v_j$ ， $s_{i,j} =0$ 。反之，对于未加权图 $s_{i,j }= 1$ 以及对于加权图， $s_{i,j}> 0$ 。
网络嵌入的目的是将图形数据映射到低维潜在空间中，其中每个顶点都表示为低维向量，并且可以直接实现网络计算。正如我们已经解释的那样，本地和全球结构都是必不可少的。然后我们首先定义一阶邻近度，它表征了本地网络的结构。
定义2。（一阶接近度）一阶接近度描述顶点之间的成对接近度。对于任何一对顶点，如果 $s_{i.j}> 0$ ，则 $v_i$ 和 $v_j$ 之间存在正一阶接近。否则， $v_i$ 和 $v_j$ 之间的一阶接近度为 $0$ 。
自然地，网络嵌入必须保持一阶接近度，因为这意味着如果现实世界中的两个顶点通过观察边链接，它们总是相似的。例如，如果一篇论文引用另一篇论文，则它们应包含一些共同的主题。但是，现实世界的数据集通常很少，以至于观察到的链接仅占一小部分。存在许多彼此相似但没有任何边链接的顶点。因此，仅捕获第一阶邻近度是不够的。我们介绍了二阶邻近度以捕获全局网络结构。
定义3.（二阶接近度）一对顶点之间的二阶接近度描述了该对邻域结构的接近度。令 $\mathcal{N}_u = \{s_{u,1}，...，s_{u,| V |}\}$ 表示 $v_u$ 与其他顶点之间的一阶接近度。然后，通过 $\mathcal{N}_u$ 和 $\mathcal{N}_v$ 的相似性确定二阶接近度。
直观地，二阶接近度假设如果两个顶点共享许多公共邻居，则它们趋于相似。这种假设已在许多领域被证明是合理的[6，14]。例如，在语言学中，如果单词始终被相似的上下文包围，它们将是相似的[6]。如果有很多普通朋友，人们就会成为朋友[14]。已经证明，二阶接近度是定义一对顶点的相似性的一个很好的度量标准，即使它们没有通过边链接[17]，因此可以高度丰富顶点的关系。因此，通过引入二阶邻近度，可以表征全局网络结构并缓解稀疏性问题。
利用一阶和二阶接近度，我们研究了在执行网络嵌入时如何同时集成它们以保留本地和全局结构的问题。这样的问题定义如下：
定义4.（网络嵌入）给定一个表示为 $G =(V,E)$ 的图，网络嵌入旨在学习映射函数 $f：v_i \longmapsto y_i∈\mathbb{R}^d$ ，其中 $d \ll | V |$ 。该函数的目的是明确使 $y_i$ 和 $y_j$ 之间的相似性保留 $v_i$ 和 $v_j$ 的一阶和二阶接近度。

3.2 The Model

3.2.1 Framework

在本文中，我们提出了一种半监督的深度模型来进行表单网络嵌入，其框架如图2所示。详细地，为了捕获高度非线性的网络结构，我们提出了一种深度结构，该结构由多个非线性映射功能可将输入数据映射到高度非线性的潜在空间以捕获网络结构。此外，为了解决结构保留和稀疏性的问题，我们提出了一个半监督模型来利用二阶和一阶邻近性。对于每个顶点，我们都能获得其邻域。因此，我们通过重构每个顶点的邻域结构来设计无监督组件，以保留二阶邻近度。同时，对于节点对的一小部分，我们可以获得它们的成对相似性，即一阶邻近度。因此，我们设计监督组件以利用一阶接近度作为监督信息来细化潜在空间中的表示。通过在建议的半监督深度模型中共同优化它们，SDNE可以很好地保留高度非线性的局部全局网络结构，并且对于稀疏网络具有鲁棒性。在接下来的部分中，我们将详细介绍如何实现半监督深度模型。

3.2.2 Loss Functions

在介绍损失函数之前，我们在表1中定义了一些术语和符号，将在以后使用。注意，以上参数表示解码器的参数。
在这里插入图片描述
现在我们介绍半监督模型的损失函数。我们首先描述无监督组件如何利用二阶邻近性来保留全局网络结构。
二阶接近度是指一对顶点的邻居引擎罩结构有多相似。因此，要对二阶接近度进行建模，就需要对每个顶点的邻域进行建模。给定网络 $G =(V,E)$ ，我们可以获得其邻接矩阵 $S$ ，其中包含 $n$ 个实例 $s_1，...，s_n$ 。对于每个实例 $\mathbf{s}_{i}=\left\{s_{i, j}\right\}_{j=1}^{n}$ ，当且仅当 $v_i$ 与 $v_j$ 之间存在链接时， $s_{i,j}> 0$ 。因此， $s_i$ 描述了顶点 $v_i$ 的邻域结构，而 $S$ 提供了每个顶点的邻域结构的信息。使用 $S$ ，我们扩展了传统的深度自动编码器[23]，以保留二阶接近度。
考虑到独立性，我们简要回顾一下深度自动编码器的关键思想。它是一种无监督的模型，由编码器和解码器两部分组成。编码器由多个非线性函数组成，这些函数将输入数据映射到表示空间。解码器还包含多个非线性函数，这些函数将表示空间中的表示映射到重构空间。然后给定输入 $x_i$ ，每层的隐藏表示如下所示:
$\begin{aligned} &\mathbf{y}_{i}^{(1)}=\sigma\left(W^{(1)} \mathbf{x}_{i}+\mathbf{b}^{(1)}\right)&(1) \\ &\mathbf{y}_{i}^{(k)}=\sigma\left(W^{(k)} \mathbf{y}_{i}^{(k-1)}+\mathbf{b}^{(k)}\right), k=2, \ldots, K& \end{aligned}$
在获得 $y_i(K)$ 之后，我们可以通过逆转编码器的计算过程来获得输出 $\hat{x}_i$ 。自动编码器的目标是最小化输出和输入的重构误差。损失函数如下所示：
定输入 $x_i$ ，每层的隐藏表示如下所示:
$\mathcal{L}=\sum_{i=1}^n ||\hat{x}_i-x_i||^2_2\hspace{1cm}(2)$
正如[23]所证明的，尽管最小化重建损失并没有明确保留样本之间的相似性，但是重建准则可以平滑地捕获数据流形，从而保留样本之间的相似性。然后考虑我们的情况，如果我们使用邻接矩阵 $S$ 作为自动编码器的输入，即 $x_i = s_i$ ，则由于每个实例si都表征了顶点 $v_i$ 的邻域结构，因此重构过程将使具有相似邻域结构的顶点具有类似的潜在表示。
然而，由于网络的某些特定特性，这种重建过程不能直接应用于我们的问题。在网络中，我们可以观察到一些链接，但同时未观察到许多合法链接，这意味着顶点之间的链接确实表明了它们的相似性，但没有链接不一定表明它们的相异性。此外，由于网络的稀疏性，S中非零元素的数量远远少于零元素的数量。然后，如果我们直接使用S作为传统自动编码器的输入，则更容易在S中重建零元素。但是，这不是我们想要的。为了解决这个问题，我们对非零元素的重构误差施加了比零元素更大的惩罚。修改后的目标函数如下所示：
$\begin{aligned} \mathcal{L}_{2nd} & = \sum_{i=1}^{n}||(\hat{x}_i-x_i)\bigodot b_i||_2^2&(3) \\ &=||(\hat{X}-X)\bigodot B||_2^2 \end{aligned}$
其中 $\bigodot$ 为哈达玛积， $b_i=\{b_{i,j}\}_{j=1}^n$ ，如果 $s_{i,j}=0$ ，则 $b_{i,j}=1$ ，否则 $b_{i,j}=\beta>0$
现在，通过使用带有邻接矩阵 $S$ 作为输入的经修订的深度自动编码器，具有相似邻域结构的顶点将在表示空间中映射，由重构准则保证。换句话说，我们模型的无监督组件可以通过重构顶点之间的二阶接近度来保留全局网络结构。
不仅需要保留全局网络结构，而且对于捕获本地结构也是必不可少的。我们使用一阶邻近度来表示本地网络结构。一阶接近度可以看作是受监管的信息，以约束一对顶点的潜在表示的相似性。因此，我们设计了受监督的组件以利用一阶接近度。为此目标的损失函数定义如下: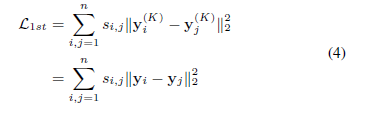
在这里插入图片描述
方程4的目标函数借用了Laplacian特征图[1]的想法，当相似的顶点在嵌入空间中映射得很远时，就会产生惩罚。一些关于社交网络的著作[13]也使用了类似的想法。我们在将思想纳入深度模型的方面进行区分，以使通过边链接的顶点在嵌入空间中映射得更近。结果，该模型保留了一阶接近度。
为了同时保留一阶和二阶接近度，我们提出了一个半监督模型，该模型结合了等式4和等式3和关节最小化以下目标功能：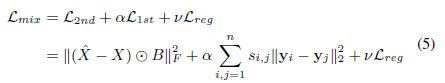
在这里插入图片描述
其中 $L_{reg}$ 是防止过度拟合的 $L_2$ 范数正则项，其定义如下：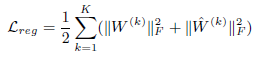

3.2.3 Optimization

To optimize the aforementioned model

3.3 Analysis and Discussions

4. EXPERIMENTS

4.1 Datasets

4.2 Baseline Algorithms

4.3 Evaluation Metrics

4.4 Parameter Settings

4.5 Experiment Results

4.5.1 Network Reconstruction

4.5.2 Multi-label Classification

4.5.3 Link Prediction

4.5.4 Visualization

4.6 Parameter Sensitivity

5. CONCLUSIONS

来源：CSDN

作者：edwinhaha

链接：https://blog.csdn.net/edwinhaha/article/details/103842271

标签

深度学习

网络模型

网络结构

监督学习

重构

非线性

2016-Structural Deep Network Embedding

文章目录