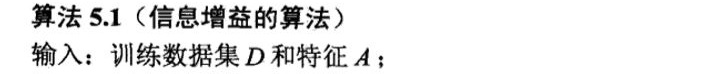05 决策树——Python实现相应算法

一、使用的数据集为：

二、《统计学习方法》中列出的算法：

1. 算法5.1（信息增益的算法）
（1）算法思想：


（2）python实现：

# author yuxy
#求信息增益的算法
#结果为：各个特征对应的信息增益为：[0.08300749985576883, 0.32365019815155627, 0.4199730940219749, 0.36298956253708536]
import  numpy as np
def information_gain(dataSet, ASet):
    """
    求一个数据集的信息增益
    :param dataSet: 数据集
    :param ASet: 特征集
    :return: 返回各个特征对应的信息增益
    """
    ig=[0]*len(ASet)
    #1 经验熵H(D)
    k=set(dataSet[4])  #记录类别
    mark=[0]*len(k)
    for i in range(len(k)):
        p=k.pop()
        sum = 0
        for j in range(len(dataSet[0])):
            if dataSet[4][j] ==p :
                sum=sum+1
        mark[i] = sum
    hd=0
    for i in range(len(mark)):
        p = (mark[i]*1.0)/len(dataSet[0])
        hd = hd -p * np.log2(p)

    #2 经验条件熵
    A = []  #记录各个特征的取值情况
    for i in range(len(ASet)):
        A1 = set(dataSet[i])
        list1=list(A1)
        A.append(list1)
    for t in range(len(A)):
        s=0.0
        for q in range(len(A[t])):
            p = A[t][q]
            sum=0.0
            ck=0.0
            for j in range(len(dataSet[t])):
                if dataSet[t][j] == p:
                    sum=sum+1
                    if dataSet[4][j]==1:
                        ck=ck+1
            t1 = sum / len(dataSet[4])
            if (sum-ck) == 0:
                t2=0
            else:
                t2 = (ck / sum) * np.log2(ck / sum) + ((sum - ck) / sum) * np.log2((sum-ck)/sum)
            s=s-t1*t2
        ig[t] =hd-s
    return ig


if __name__=='__main__':
    dataSet=[[1,1,1,1,1,2,2,2,2,2,3,3,3,3,3],[2,2,1,1,2,2,2,1,2,2,2,2,1,1,2],
             [2,2,2,1,2,2,2,1,1,1,1,1,2,2,2],[1,2,2,1,1,1,2,2,3,3,3,2,2,3,1],
             [2,2,1,1,2,2,2,1,1,1,1,1,1,1,2]]
    ASet={'age', 'job', 'house', 'credit'}
    print('各个特征对应的信息增益为：%s' % information_gain(dataSet, ASet))

2. 算法5.2（ID3算法）
（1）算法思想：


（2）python代码：

# author yuxy
import operator
import math

#构造数据集
def createDataSet():
    dataSet = [[1, 2, 2, 1,'no'], [1, 2, 2, 2,'no'], [1, 1, 2, 2,'yes'], [1, 1, 1, 1,'yes'], [1, 2, 2, 1,'no']
               , [2, 2, 2, 1,'no'], [2, 2, 2, 2,'no'], [2, 1, 1, 2,'yes'], [2, 2, 1, 3,'yes'], [2, 2, 1, 3,'yes']
               , [3, 2, 1, 3,'yes'], [3, 2, 1, 2,'yes'], [3, 1, 2, 2,'yes'], [3, 1, 2, 3,'yes'], [3, 2, 2, 1,'no']]
    features = ['age','job','house','credit']
    return dataSet,features

#构造决策树
def treeGrowth(dataSet, features):
    #设置递归返回条件
    classList=[example[-1] for example in dataSet]      #取最后一列，下标为-1时代表最后（最后一行或者最后一列）
    if classList.count(classList[0])==len(classList):   #数据集中全部都是一个类别时，count函数表示计数
        return classList[0]
    if len(dataSet[0])==1:     #没有更多的特征
        return classify(classList)

    #进行递归
    #设置根节点
    bestFeat=findBestSplit(dataSet)   #确定最佳分裂特征的下标
    bestFeatLabel=features[bestFeat]  #确定最佳特征
    myTree={bestFeatLabel:{}}
    featValues=[example[bestFeat] for example in dataSet]   #选择出的最好的属性的取值
    uniqueFeatValues=set(featValues)
    del(features[bestFeat])           #删除掉该属性
    #设置多个子树
    for values in uniqueFeatValues:
        subDataSet=splitDataSet(dataSet,bestFeat,values)
        myTree[bestFeatLabel][values]=treeGrowth(subDataSet,features)  #每个分支创建一颗子树
    return myTree

#当没有多余的feature，并且剩下的样本不完全是一样的类别时，采用多数表决
def classify(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote]=0
        classCount[vote]+=1
    sortedClassCount=sorted(classCount,key=operator.itemgetter(1),reverse=True)
    #.iteritems()将字典中所有项以列表呈现，  operator.itemgetter(1)以哪一维进行排序
    return sortedClassCount[0][0]

#寻找用于分裂的最佳属性（遍历所有属性，计算信息增益，最大的为最好的分裂属性）
def findBestSplit(dataSet):
    numFeatures=len(dataSet[0])-1
    baseEntropy=calcShannonEnt(dataSet)
    bestInfoGain=0.0
    bestFeat=-1
    for i in range(numFeatures):
        featValues=[example[i] for example in dataSet]
        uniqueFeatValues=set(featValues)
        newEntropy=0.0
        for val in uniqueFeatValues:
            subDataSet=splitDataSet(dataSet,i,val)
            prob=len(subDataSet)/float(len(dataSet))
            newEntropy+=prob*calcShannonEnt(subDataSet)
        if (baseEntropy-newEntropy)>bestInfoGain:
            bestInfoGain=baseEntropy-newEntropy
            bestFeat=i
    return bestFeat

#选择完分裂属性以后，就进行数据集的分裂
def splitDataSet(dataSet,feat,values):
    retDataSet=[]
    for featVec in dataSet:
        if featVec[feat]==values:
            reduceFeatVec=featVec[:feat]
            reduceFeatVec.extend(featVec[feat+1:])
            retDataSet.append(reduceFeatVec)
    return retDataSet

#计算数据集的熵
def calcShannonEnt(dataSet):
    numEntries=len(dataSet)
    labelCounts={}
    for featVec in dataSet:
        currentLabel=featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel]=0
        labelCounts[currentLabel]+=1
    shannoEnt=0.0

    for key in labelCounts:
        prob=float(labelCounts[key])/numEntries
        if prob!=0:
            shannoEnt-=prob*math.log(prob,2)
    return shannoEnt

#根据上面构造的决策树进行数据分类
def predict(tree,newObject):
    while isinstance(tree,dict):
        key=tree.keys()[0]
        tree=tree[key][newObject[key]]
    return tree

if __name__ == '__main__':
    dataSet,features=createDataSet()
    tree=treeGrowth(dataSet,features)
    print(tree)

来源：CSDN

作者：yuxy411

链接：https://blog.csdn.net/yuxy411/article/details/103734081