微积分：2.2泰勒公式函数极值定积分

文章目录

• 任务详解：
• 1.泰勒公式
• 2.函数的凹凸性
• 3.函数的极值
• 4.不定积分（求原函数）
• 第一类换元法（凑微分）
• 第二类换元法
• 分部积分法
• 5.定积分
• 牛顿莱布尼茨公式
• 换元法
• 分部积分

本课程来自深度之眼，部分截图来自课程视频。
【第二章 微积分】2.2泰勒公式函数极值定积分
在线LaTeX公式编辑器

任务详解：

这节课主要介绍了泰勒公式，函数的凹凸性，函数的极值，不定积分，定积分等知识点。
掌握目标：
1、了解泰勒公式
2、了解函数的凹凸性
3、掌握函数的极值，以及极值的充要条件
4、掌握不定积分，定积分的计算，第一第二类换元，分部积分法，牛顿莱布尼茨公式

1.泰勒公式

泰勒（Taylor）中值定理1：如果函数$f(x)$在$x_0$处具有n阶导数，那么存在$x_0$的一个邻域，对于该邻域内的任一$x$，有
$f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+...+\frac{f^{n}(x_0)}{n!}(x-x_0)^n+R_n(x)$
其中：
$R_n(x)=o((x-x_0)^n)$
说人话：这个定理就是任意一个函数$f(x)$，都可以在$x_0$展开，写成一个多项式的模式，最后一项就是误差$R_n(x)$，是x到$x_0$的高阶无穷小（佩亚诺余项）。
泰勒（Taylor）中值定理2：如果函数$f(x)$在$x_0$的某个邻域$U(x_0)$内具有(n+1)阶导数，那么对任一$x\in U(x_0)$，有
$f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+...+\frac{f^{n}(x_0)}{n!}(x-x_0)^n+R_n(x)$
其中：
$R_n(x)=\frac{f^{n+1}(\xi)}{(n+1)!}(x-x_0)^{n+1}$
$\xi$是$x_0$与$x$之间的某个值，这项也叫：拉格朗日余项
当×0=0时，称为麦克劳林展开
例子（略）

2.函数的凹凸性

定义：设$f(x)$在区间$I$上连续，如果对$I$上任意两点$x_1,x_2$恒有
$f\left(\frac{x_1+x_2}{2}\right)<\frac{f(x_1)+f(x_2)}{2}$
那么称$f(x)$在$I$上的图形是（向上）凹的（或凹弧）；如果恒有
$f\left(\frac{x_1+x_2}{2}\right)>\frac{f(x_1)+f(x_2)}{2}$
那么称$f(x)$在$I$上的图形是（向上）凸的（或凸弧）.
如果函数$f(x)$在$I$内具有二阶导数，那么可以利用二阶导数的符号来判定曲线的凹凸性，这就是下面的曲线凹凸性的判定定理：
定理2：设$f(x)$在[a，b]上连续，在(a,b)内具有一阶和二阶导数，那么
（1）若在(a,b)内$f^n(x)>0$，则$f(x)$在[a,b]上的图形是凹的；
（2）若在(a,b)内$f^n(x)<0$，则$f(x)$在[a,b]上的图形是凸的.
证明：
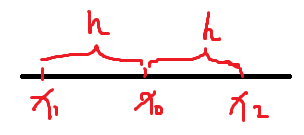
设$x_1$和$x_2$为[a,b]类任意两点，且$x_1<x_2$，记$\frac{x_1+x_2}{2}=x_0$，并记$x_2-x_0=x_0-x_1=h$，则$x_1=x_0-h$，$x_2=x_0+h$

由拉格朗日中值公式可得：
$f(x_0+h)-f(x_0)=f'(\xi_1)(x_0+h-x_0)=f'(x_0+\theta_1h)h,0<\theta_1<1\tag{1}$
$f(x_0)-f(x_0-h)=f'(\xi_2)(x_0-x_0+h)=f'(x_0-\theta_2h)h,0<\theta_2<1\tag{2}$
上面由于$\xi_1$是在$x_0$到$x_0+h$之间的，所以可以写成最后那个样子$(\xi_1=x_0+\theta_1h$是等价的，$\xi_2$同理。
等式（1）减（2）得：
$f(x_0+h)+f(x_0-h)-2f(x_0)=[f'(x_0+\theta_1h)-f'(x_0-\theta_2h)]h\tag{3}$
对等式（3）中的$f'(x_0+\theta_1h)-f'(x_0-\theta_2h)$再来一次拉格朗
日
中值公式：
$f'(x_0+\theta_1h)-f'(x_0+\theta_2h)=f''(\xi_3)(x_0+\theta_1h-x_0+\theta_2h)$$=f''(\xi_3)(\theta_1+\theta_2)h\tag{4}$
将（4）带入（3）：
$f(x_0+h)+f(x_0-h)-2f(x_0)=f''(\xi_3)(\theta_1+\theta_2)h^2\tag{5}$
对于定理的第一种情况
（1）若在(a,b)内$f^n(x)>0$，则$f(x)$在[a,b]上的图形是凹的；
我们可以由$f''(\xi_3)>0，(\theta_1+\theta_2)>0,h^2>0$，对公式(5)判断：整体大于0，即：
$f(x_0+h)+f(x_0-h)-2f(x_0)>0$
把$x_1=x_0-h$，$x_2=x_0+h$，$\frac{x_1+x_2}{2}=x_0$带回去
$f(x_2)+f(x_1)>2f(\frac{x_1+x_2}{2})$
证明完毕
$f\left(\frac{x_1+x_2}{2}\right)<\frac{f(x_1)+f(x_2)}{2}$
情况二类似。

3.函数的极值

定义设函数$f(x)$在点$x_0$的某邻域$U(x_0)$内有定义，如果对于去心邻域$\overset{o}{U}(x_0)$内的任一x，有
$f(x)<f(x_0)(或f(x)>f(x_0))$
说人话：就是$x_0$比附近所有的x的值都大（小）。
那么就称$f(x_0)$是函数$f(x)$的一个极大值（或极小值）.

定理1（必要条件）：设函数$f(x)$在$x_0$处可导，且在$x_0$处取得极值，则$f'(x)=0$

定理2（第一充分条件）：设函数$f(x)$在$x_0$处连续，且在$x_0$的某去心邻域$\overset{o}{U}(x_0,\delta)$内可导.
（1）若$x\in (x_0-\delta,x_0)$时，$f'(x)>0$，而$x\in (x_0,x_0+\delta)$时，$f'(x)<0$，则$f(x)$在$x_0$处取得极大值；
说人话：在x的左边导数大于0（函数递增），右边导数小于0（函数递减）.
（2）若$x\in (x_0-\delta,x_0)$时，$f'(x)<0$，而$x\in (x_0,x_0+\delta)$时，$f'(x)>0$，则$f(x)$在$x_0$处取得极小值；
（3）若$x\in \overset{o}{U}(x_0,\delta)$时，$f'(x)$的符号保持不变，则$f(x)$在$x_0$处没有极值。

定理3（第二充分条件）：设函数$f(x)$在$x_0$处具有二阶导数且$f'(x_0)=0$，
$f''(x_0)\neq0$，则
（1）当$f''(x_0)<0$时，函数$f(x)$在$x_0$处取得极大值；
（2）当$f''(x_0)>0$时，函数$f(x)$在$x_0$处取得极小值.
这个定理3是根据函数的凹凸性来进行判断了，也可以用泰勒展开式来进行判断。

4.不定积分（求原函数）

定义1：如果在区间$I$上，可导函数$F(x)$的导函数为$f(x)$，即对任一$x\in I$，都有
$F'(x)=f(x)或dF(x)=f(x)dx$，那么函数F（x）就称为$f(x)（或f(x)dx）$在区间$I$上的一个原函数
定义2：在区间$I$上，函数$f(x)$的带有任意常数项的原函数称为$f(x)$（或$f(x)dx$）在区间$I$上的不定积分，记作
$\int f(x)dx$
其中记号$\int$称为积分号，$f(x)$称为被积函数，$f(x)dx$称为被积表达式，$x$称为积分变量。
由此定义及前面的说明可知，如果$F(x)$是$f(x)$在区间$I$上的一个原函数，那么$F(x)+C$就是$f(x)$的不定积分，即
$\int f(x)dx=F(x)+C$
性质1：设函数$f(x)$及$g(x)$的原函数存在，则：
$\int[f(x)+g(x)]dx=\int f(x)dx+\int g(x)dx$
性质2：设函数$f(x)$的原函数存在，k为非零常数，则
$\int kf(x)dx=k\int f(x)dx$

第一类换元法（凑微分）

定理1:设$f(u)$具有原函数，$u=\varphi(x)$可导，则有换元公式
$\int f[\varphi(x)]\varphi'(x)dx=\left [\int f(u)du\right]_{u=\varphi(x)}$
例子：求$\int 2cos2xdx$
$\int 2cos2xdx=\int cos2xd2x$
令$u=2x$
$\int cos2xd2x=\int cosudu=sinu+C$
带回$u=2x$
$\int 2cos2xdx=sin2x+C$

第二类换元法

定理2：设$x=\psi(t)$是单调的可导函数，并且$\psi'(t)\neq0.$又设$f[\psi(t)]\psi'(t)$具有原函数，则有换元公式
$\int f(x)dx=\left [\int f[\psi(t)]\psi'(t)dt\right]_{t=φ^{-1}(x)}$
其中$φ^{-1}(x)$是$x=\psi(t)$的反函数.

分部积分法

$\int udv=uv-\int vdu$
例子：求$\int xcosxdx$
$\int xcosxdx=\int x dsinx=xsinx-\int sinxdx=xsinx+cosx+C$

5.定积分

定积分的意义：曲线的面积

在区间[a,b]中任意插入若干个分点
$a=x_0<x_1<x_2<……<x_{n-1}<x_n=b$
把[a,b]分成n个小区间
$[x_0,x_1],[x_1,x_2],…,[x_{n-1},x_n]$
它们的长度依次为
$\Delta x_1=x_1-x_0,\Delta x_2=x_2-x_1,...,\Delta x_n=x_n-x_{n-1}$
面积A为：
$A\approx f(\xi_1)\Delta x_1+f(\xi_2)\Delta x_2+...+f(\xi_n)\Delta x_n=\sum_{i=1}^nf(\xi_i)\Delta x_i$
其中$\xi_i$是在$x_{i-1}\sim x_i$区间的任意一个值。
为了保证所有小区间的长度都无限缩小，我们要求小区间长度中的最大者趋于零，如记$\lambda=max|\Delta x_1, \Delta x_2,…,\Delta x_n|$，则上述条件可表示为$\lambda \to0$.当$\lambda \to0$时（这时分段数n无限增多，即$n\to \infty$），取上述和式的极限，便得曲边梯形的面积
$A=\lim_{\lambda\to0}\sum_{i=1}^nf(\xi_i)\Delta x_i$
$\int_a^bf(x)dx=I= \lim_{\lambda\to0}\sum_{i=1}^nf(\xi_i)\Delta x_i$

牛顿莱布尼茨公式

定理3（微积分基本定理）如果函数$F(x)$是连续函数$f(x)$在区间[a,b]
上的一个原函数，那么
$\int_a^bf(x)dx=F(b)-f(a)$

换元法

分部积分

例子：
$\int_0^1xe^{-x}dx=\int_0^1-xde^{-x}=\left[-xe^{-x}\right]_0^1-\int_0^1e^{-x}d{-x}$
$=(-1e^{-1})-\int_1^0e^udu=-e^{-1}-[e^u]_1^0=e^{-1}-1+e$

来源：CSDN

作者：oldmao_2001

链接：https://blog.csdn.net/oldmao_2001/article/details/103710418