K-近邻算法（KNN）

1. 原理

• 定义
  如果一个样本的特征空间中的K个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。
  K值取的过小，容易受到异常点的影响
  K值取的过大，容易受到样本不均衡的影响

• 距离公式

  欧式距离：
  
  曼哈顿距离（绝对值距离）：
  

2. K-近邻算法API

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')

 - n_neighbors：K值 ,int,可选 (默认= 5)，k _neighbors查询默认使用的邻居数
 - algorithm: {'auto', 'ball_tree', 'kd_tree'， 'brute'}, 可选用于计算最近邻居的算法: 
                 'ball_ tree'将会使用BallTree， 'kd_tree'将使用KDTree。
                 'auto'将 尝试根据传递给fit方法的值来决定最合适的算法。(不同实现方式影响效率)

3. 案例：鸢尾花种类预测

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
def knn_iris():
    # 1)获取数据
    iris = load_iris()
    # 2) 划分数据集
    x_train, x_test, y_train, y_test=train_test_split(iris.data, iris.target,random_state=6)
    # 3) 特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 4) KNN算法预估流程
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train,y_train)
    # 5) 模型评估
    #方法1 直接比对 真实值和预测值
    y_predict = estimator.predict(x_test)
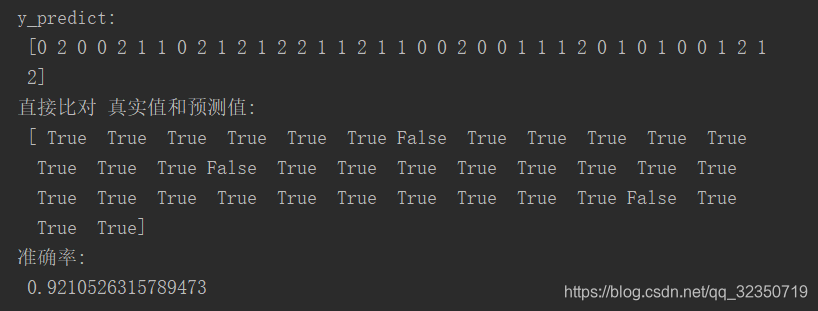
    print("y_predict:\n", y_predict)
    print("直接比对 真实值和预测值:\n", y_test==y_predict)
    #方法2 计算准确率
    score = estimator.score(x_test,y_test)
    print("准确率:\n",score)

knn_iris()

4. K-近邻总结
优点：简单、易于理解、易于实现、无需训练
缺点：

• 懒惰算法，对测试样本分类时计算量大，内存开销大
• 必须指定K值，K值选择不当则分类精度不能保证

使用场景：小数据场景，几千~几万样本

来源：https://blog.csdn.net/qq_32350719/article/details/99449339