题目:
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-common-subsequence
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
输入:text1 = “abcde”, text2 = “ace”
输出:3
解释:最长公共子序列是 “ace”,它的长度为 3。
暴力算法,常规思路
从样例输入输出入手,输入两个字符串:abcde/ace。
按照字符串角标走的话,从左往右,角标同时想有移动,遇到相同字符则最长公共子序列+1。
两个字符串角标分别是i,j,如果i=0,j=0,那么我们可以知道s1[0]=s2[0],这时公共最长子序列有了字母a,那么剩下需要判断的则是 bcde 和 ce的公共最长子序列。
让i,j同时+1明显是不行的。
肉眼可以看到在剩下要判断的字符串中 s[2]是"c" s[1]是"c"。
也就是如果让i=i+1, j=j 是可以顺利找到下一个相同字符的。可是我们计算机不知道。
假象另一种情况 ,如果两个字符串是acbde afce,那么 i=i, j=j+1就能让我们找到下一个相同字符。
所以这里要同时计算 i=i, j=j+1 和 i=i+1, j=j 看哪种情况最终返回的长度大。
图解为
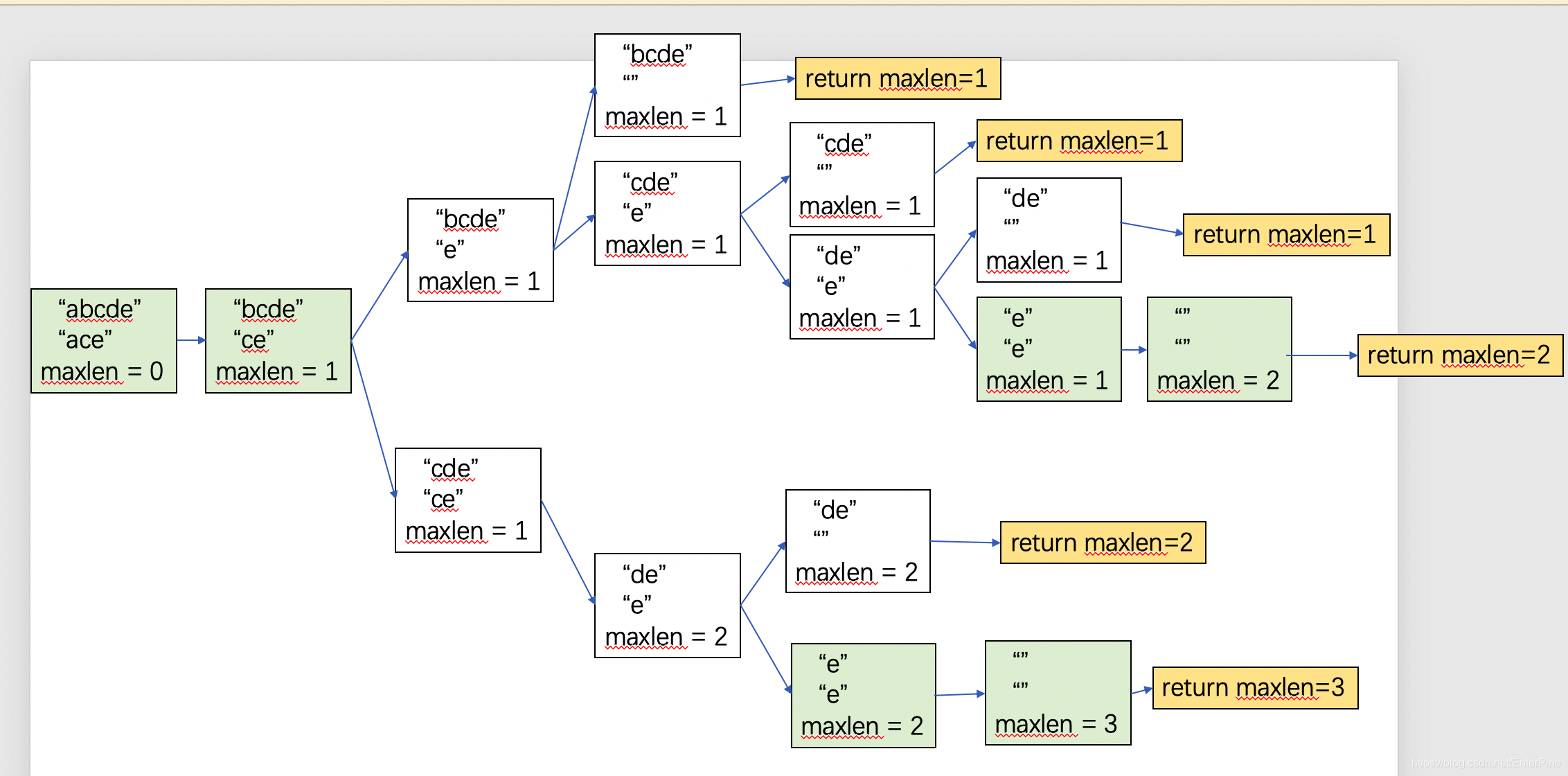
明显,这种算法效率为O(2^N)
下面是编码:
import static java.lang.Math.max;
public class LeetCode1143 {
public static int dp(String text1,String text2,int maxlen){
if(text1.charAt(0) == text2.charAt(0)){
String ttext1 = text1.substring(1,text1.length());
String ttext2= text2.substring(1,text2.length());
maxlen = maxlen + 1;
if(ttext1.length()>0 && ttext2.length()>0) {
return dp(ttext1, ttext2, maxlen);
}
}
else{
if(text1.length()>0 && text2.length()>0) {
String ttext1 = text1.substring( 1, text1.length());
String ttext2 = text2.substring(0, text2.length());
String ttext11 = text1.substring(0, text1.length());
String ttext22 = text2.substring(1, text2.length());
if(ttext1.length() == 0 && ttext22.length()>0){
return dp(ttext11, ttext22, maxlen);
}
if(ttext22.length() == 0 && ttext1.length() > 0 ){
return dp(ttext1, ttext2, maxlen);
}
if(ttext22.length() > 0 && ttext1.length() > 0) {
return max(dp(ttext11, ttext22, maxlen), dp(ttext1, ttext2, maxlen));
}
}
}
return maxlen;
}
public static int longestCommonSubsequence(String text1, String text2) {
int a = dp(text1,text2,0);
return a;
}
public static void main(String[] args){
// String s1 = "abcde";
//// String s2 = "ace";
String s1 = "pmjghexybyrgzczy";
String s2 ="hafcdqbgncrcbihkd";
int a = longestCommonSubsequence(s1,s2);
System.out.println(a);
}
}
以上代码是可以找到正确答案的,但是由于是深度搜索的思路,效率非常差,提交后会显示超时。
以上为从左向右深度搜索所有情况,当找到两个相同的字符时,最大长度+1,然后继续向后按照各种情况查找。
优化后的算法,使用动态规划提高效率
上述算法的缺点是,使用了深度优先搜索的思想,将所有查找方式都遍历一遍才找到最大长度。
当找到两个相同字符的时候,让相同字符前的最大长度+1。
例如:
abcde
ace
当我找到c=c的时候,那么最大长度应该是ab 与 a的最大子序列长度+1。
再例如,当我找到e=e的时候,那么最大长度应该是abcd 与 ac的最大子序列长度+1。
也就有了这样的模型。
有一个数组dp[][]
dp[i][j] 表示 s1的0~i 与s2的0~j 两个子串的最长公共子序列。
那么当 s[i]=s[j]的时候 dp[i][j]=dp[i-1][j-1]+1
当 s[i]<>s[j]的时候,那么dp[i][j]的值若想要代表当天位置的最长子序列,我们把角标各自往前推一步,取较大的值。
dp[i][j]=max(dp[i-1][j],dp[i][j-1])

代码实现:
package com.jinsong.leetcode;
public class LeetCode1143_ac {
public static int longestCommonSubsequence(String text1, String text2) {
int[][] dp = new int[text1.length()+1][text2.length()+1];
//表示text1[0~i] text2[0~j]的最大子序列长度
for(int i = 0 ;i<text1.length()+1;i++){
dp[i][0]=0;
}
for(int i = 0 ;i<text2.length()+1;i++){
dp[0][i]=0;
}
for(int i=0;i<text1.length();i++){
for(int j=0;j<text2.length();j++){
if(text1.charAt(i)==text2.charAt(j)){
dp[i+1][j+1]=dp[i][j]+1;
}
else{
dp[i+1][j+1]=java.lang.Math.max(dp[i][j+1],dp[i+1][j]);
}
}
}
return dp[text1.length()][text2.length()];
}
public static void main(String[] args){
String s1 = "pmjghexybyrgzczy";
String s2 = "hafcdqbgncrcbihkd";
int a = longestCommonSubsequence(s1,s2);
System.out.println(a);
}
}
来源:CSDN
作者:EnterPine
链接:https://blog.csdn.net/EnterPine/article/details/103476203