目录
概览
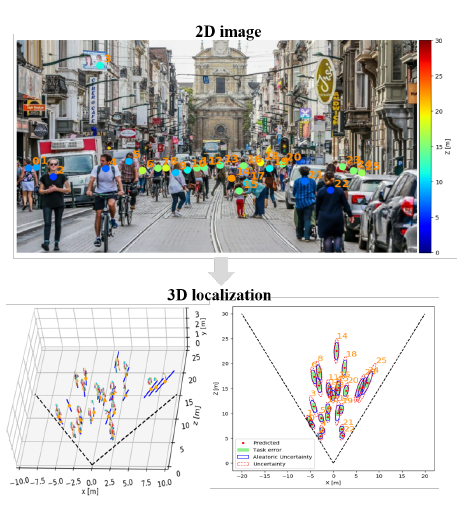
近日在阅读"MonoLoco: Monocular 3D Pedestrian Localization and Uncertainty Estimation"文献,旨在解决定位图像中行人位置(本质上只预测距离),文献主要采用基于开源框架提取单目视觉图像中的人体骨架信息,再通过轻量级的全连接神经网络对行人的方位进行预测,并对方位预测的不确定度进行了评估和可视化。
HighLights
- task-error:task-error是一种确定的不确定性,是由于任务抽象时对有关因素忽略而导致的不可消除误差,可被作为不确定度的下界。本文中,基于距离和身高的三角形相似性原理和欧洲人口身高的高斯分布假设,求解了定位误差(米)的task-error作为不确定判断的下界。
- 输出假设的Laplace分布:使用Laplace分布替代高斯分布作为计算数据不确定性(aleatoric uncertainty)的分布,其优势是基于距离比的分布计算,使得预测对象无论远近,误差都能被合理考虑,问题在于无法像高斯分布一样直接得到,需要采样求出。
- Geometric Baseline方法:提供了一种纯几何学的定位方法,作为baseline。
- 模型与数据不确定性估计:模型不确定性采用基于dropout的变分推理实现(由于需多次运行模型,因此称为expensive sample),数据不确定性是在由输出决定的Laplace分布上采样求方差得到(由于只需在确定的分布上采样多次,因此称为cheap sample)。
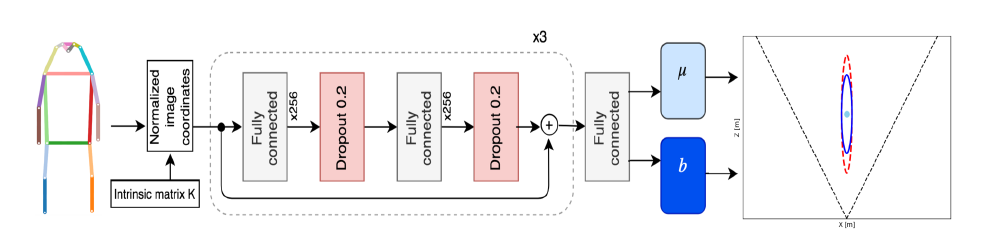
模型架构:开源工具提取单目图像人体骨架 + 相机内在矩阵正则化与中心化 + 全连接成预测Laplace分布参数。
Camera Intrinsic Matrix 笔记
在利用开源框架提取骨架信息之后,将骨架信息输入神经网络之前,模型使用了两个数据预处理手段,一是相机固定矩阵(intrinsic matrix)以避免模型对特定的相机配置过拟合,二是中心化输入的数据,使模型只考虑骨架之间的相对结果,忽略骨架在图像中的具体位置。我一直对计算机图形学中的部分内容了解不是太清楚,借着这个机会查阅学习了一下,在此做一些整理:
Camera Matrix 被分为Intrinsic和Extrinsic矩阵,常常是通过外部测量得到的结果,两者有着各自的用途,假设现在有一个理想的针孔(pinhole)照相机:

Intrinsic Matrix - K:将3D物品经过针孔投影(projection)后的坐标(3D坐标(Z轴为常量1)/2D坐标以针孔为参考系)转换到以相机底片上的2D参考系上。
Extrinsic Matrix(待求证): 刻画相机在拍摄空间中的倾向。
Intrinsic Matrix
让我们通过将胶片的2D坐标还原至针孔的3D坐标开始,在底片参考系下,考虑数字相片所存储的像素点,其2D坐标常常是以左上角为原点,序列索引组成的\((x_s,y_s)\)。
Step 1 :根据物理像素距离,将2D坐标转换为真实长度坐标,其中\(s_x,s_y\)分别表示了相机像素点在底片上的实际距离。
\[\hat X_s = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_s \\ y_s \\ 1 \end{bmatrix}\]
Step 2 :基于基向量的转换,将当前基于胶片的坐标\(\hat X_s\)变为基于针孔的坐标。转换矩阵形状3x3,为\(M_s = [R_s | c_s]\),其中\(R_s\)的对应着胶片与针孔间的旋转情况,\(c_s\)对应着胶片与针孔中心点的位移情况,具体内容不在此深究。
\[p = M_s \hat X_s\]
Step 3:对Step1和Step2过程求逆,形成Intrinsic Matrix。由于三角形相似定理,step2中算出的\(p\)坐标与针孔的3D投影坐标\(p_c\)呈正比\(p = sp_c\),因此最终由\(p_c -> (s_x,s_y)\)的过程可以如下书写:
\[ [s_x, s_y, 1]^T = \alpha M_s^{-1}p_c = Kp_c\]
因此最终求得Intrinsic Matrix K.
Hint:在这里面,正比例系数\(\alpha / s\)是规定的,其的确定需要结合针孔投影后的3D坐标尺度进行考虑,在MonoLoco文章中,利用\(K\)矩阵正则化的具体公式为\([x^*_i,y^*_j,1]^T = K^{-1}[u_i,v_i,1]^T\),我们可以看到,这里的比例系数使得常量坐标z恒为1.
小结:在论文中,通过将行人骨架信息乘以\(K^{-1}\),实际上就是将坐标脱离底片,还原至真实点经过针孔投影后的2D坐标,使得坐标只与针孔(相机间无差异)有关,而与底片(相机间有差异)信息无关。
Task-Error - 不确定性任务下确界的计算
在常见的利用变分推理进行不确定性估计的模型中,通常手段是模型预测、dropout采样等,并根据不确定度与误差的相关性以定性地证明不确定度评估的有效性。在本文中,利用简单几何学建模的手段,给出了确定的task-error(不确定性预估的下界),从而给出了一个定量的参考。。
不确定性的源头:行人身高的差异
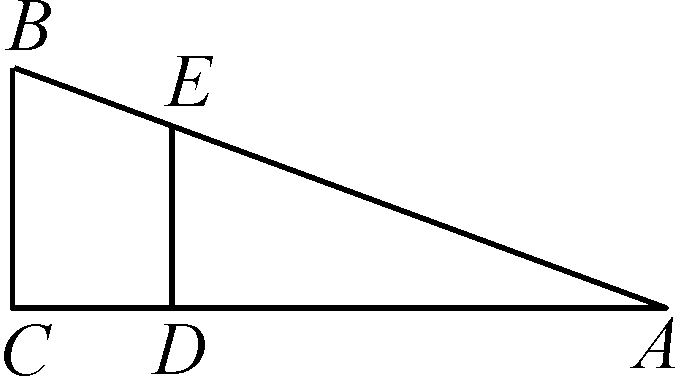
几何学中有一类经典问题:路灯打在小明身上,已知路灯和小明的身高以及两者之间的距离,求解小明影子的长度。对于拍摄得到的照片,如果所有人的尺寸(最常用的就是身高)都完全一致的话,那么机器是可以在给定尺寸条件下根据相似定理无误差地推断出距离的。但实际情况并不是这样……
建模:
- 由三角形相似定理,若以假设的固定身高测某人距离,那么误差为\(e = |d_{gt} - d_{h-mean}| = d_{gt}|1-{h_{mean} \over h_{gt}}|\)
- 对于e的期望,假定身高服从某种分布\(P(H)\),则误差期望为\(\hat e = d_{gt}E_{h \sim P(H)}[|1- {h_{mean}\over h}|]\)
- 对于分布P(H),可以有很多种假设:
- 一维高斯分布
- 男性高斯分布+女性高斯分布 -> 混合分布
- 成年男性+成年女性+青少年...
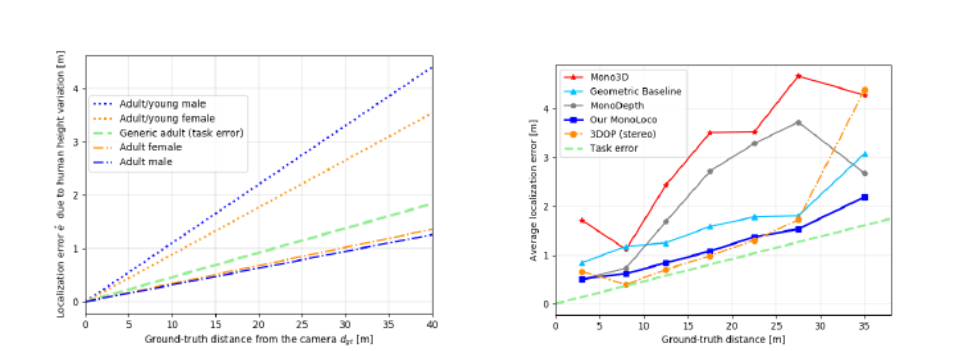
通过最终的实验,可以看出Task-Error对于不确定性下界的划定是比较准确的,并且能够定量分析模型对不确定性预测的效果。
输出假设的Laplace分布
Laplace分布形如\(L_{Laplace}(x|\mu,b) = {|1 - \mu / x|\over b}\), 其中有\(\mu\)和\(b\)两个参数,前者和正态分布一样对应着均值,但后者并不直接代表方差(只是一种对区间大小的估计),因此方差只能通过在该分布上采样并估计得到。
该分布相较于正态分布的优势在于考虑了第一视角在空间中误差比例差异大的问题,其使用的是相对比例而非绝对距离:对于过近的行人,小范围内的距离变化也将被考虑;对于过远的行人,大范围内的距离不会被过分考虑。
问题:
在文中最后所给出的epistemic+aleatoric不确定计算公式中,与前面博文中利用正态分布求不确定性有一些不同。
- 正态分布+变分推理:两类不确定性分开求解,模型不确定性需多次dropout,数据不确定性一次即可但为了统一跟随多次dropout求均值。
- 拉普拉斯+变分推理:两类不确定性一并求解,将在分布上采样和dropout采样的结果混在一起,计算方差。(经过公式推理,两者的差异在于前者计算模型不确定性时直接使用预测得到的均值,后者计算模型不确定性时使用的均值是采样求平均得到的)
Geometric Baseline 基于纯几何学的参照方法
在实验中,设计了一种Geometric Baseline作为深度学习网络效果的参照,可以理解为这种方法其实是一种传统的数学建模。在建模这个模型的过程中,使用了很多概率统计方法辅助模型选择,在此对这个方法进行简述。
假设:将所有行人考虑为固定的对象(同样身高、同样的其他身体尺寸等……)
方法:选择某种身体长度信息,使用pose detector在图像上测量其像素信息,再用相似三角形原理计算其距离相机的距离(考虑角度,进而算出真实坐标信息)。
身体长度信息的选择:该模型的重点在于选择哪一个身体指标?,为此论文中列举了三个指标:头-肩膀、肩膀-臀部,臀部-膝关节,并用统计学的方法进行选择。
- 目标:寻找对于所有人来说“尺寸尽可能固定”的指标 —— 指标真实值的方差最小。
- 指标真实值的计算:给定内在矩阵K和实例的Groud Truth位置(x,y,z),即可根据图片中该指标的长度反投影得到真实世界中指标的长度(以米为单位)。
- 统计:对所有行人都做这样的工作,分析指标的均值和方差。
- 结论:肩膀-臀部的距离在所有行人中方差最小(最稳定)。因此根据图片中肩膀-臀部的像素长度,利用几何学计算行人在真实世界中的位置。
公式总结
损失函数:基于Laplace分布的negative log-likelihood损失 + 变分推理KL散度拟合的损失
\[L_{Laplace}(x|\mu,b) = {|1 - \mu/x| \over b} + log(2b)\]
\[L_{dropout}(\theta,p_{drop}) = {1 - p_{drop} \over 2N}||\theta||^2\](高斯分布,均值为0,方差为\(\theta\))
不确定度计算:以下公式是dropout采样和Laplace采样形成的不确定总计算公式,可由两个不确定度公式合并和消除得到(注意数据不确定的方差是有Laplace采样得到的)。
\[Var(X) = {1 \over TI}\Sigma^T_{t=1}\Sigma^I_{i=1}\hat x^2_{t,i}(\mu_t,b_t) - [{1\over TI} \Sigma^T_{t=1}\Sigma^I_{i=1}\hat x_{t,i}(\mu _t, b_t)]^2\]
