Tarjan专题
由于时间关系,本文只针对Tarjan做总结。如果有对Tarjan的入门有疑问请自行百度
有向图tarjan
在有向图中跑tarjan,通常都是求强连通分量(其中的所有点都可以间接直接到达)。一个点也算强连通。
设当前的节点为 \(u\) ,它的儿子节点为 \(v\) ,如果 \(v\) 没有被访问,那么时间戳戳一个,low[u]=min(low[u],low[v]) 。如果被访问过,那么low[u]=min(low[u],dfn[v]) 。这里必须用一个栈来保存强连通及其大小。当一个点访问玩所有的儿子后,还有 dfn[u]==low[u] ,那么在这个栈里面的元素就都是强连通分量。因为我们dfs是是以树枝边进行遍历的。如果 \(u\) 能到达的最早的节点都只有它自己,那么它的儿子更没有机会遍历到前面的节点。输出强连通只需输出栈内元素即可。
缩点
求了强连通之后,将强连通变成一个点,那么整张图就变成了有向无环图。我们就可以在上面做一些拓扑序之类的问题了。
无向图tarjan
无向图有一些改变。边从有向变成了无向,任意两点只要连边就可以到达。所以在无向图上求强连通是没有意义的。
在无向图上一般求割点与桥。
顾名思义,干掉割点,其他的点就无法全部连通,干掉桥,其他的点也无法全部连通。见图:
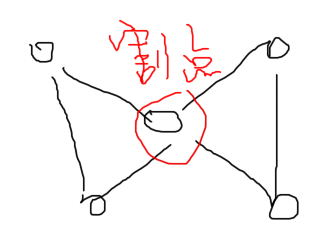
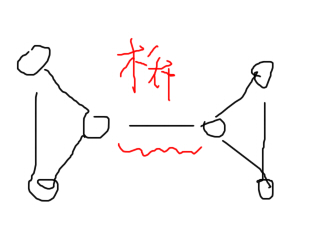
对于割点,我们可以发现:存在 dfn[u]<=low[v] 。如果不存在,那么其儿子都可以通过后向边访问到比 \(u\) 更靠前的节点。在根节点时会有些不同。如果在根节点需要做超过1次dfs(不是超过1棵子树),那么根就是割点。
对于桥,也可以发现:dfn[u]<low[v]。注意,这里和上面有点不同。这里不可以取等。因为这是桥,那么 \(u\) 的孙子一定只能通过 \(v\) 到达 \(u\) 。low[v]==dfn[v]。