ML(9) - EnsembleLearing集成学习

集成学习

• 集成学习基本概念
• Bagging
• 基本概念
• Scikit-learn中的Bagging
• 随机森林
• Boosting
• 基本概念
• Scikit-learn中的Boosting
• 集成学习结合策略
• 集成学习回归问题

---

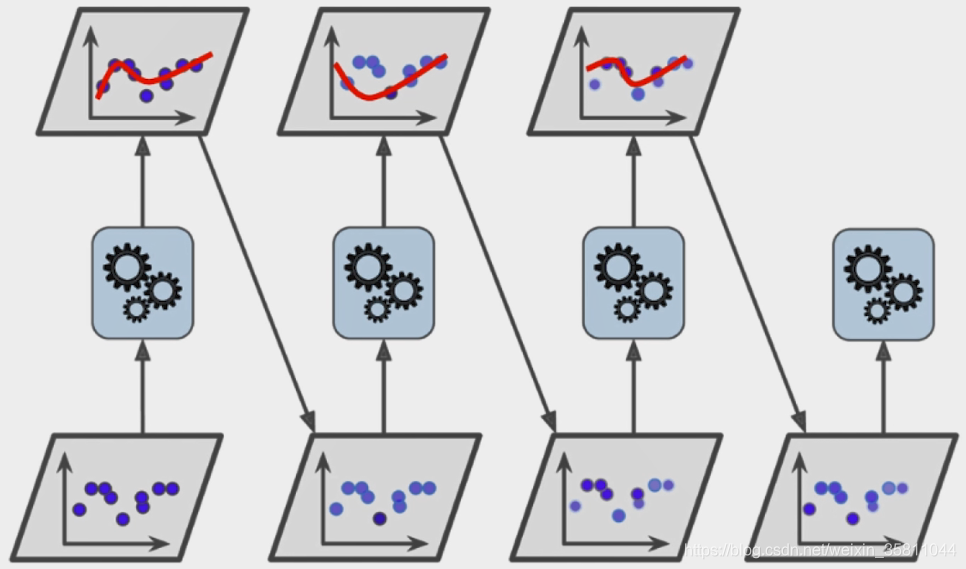
集成学习基本概念

• 训练多个学习器，对同一样本预测，再用某种结合策略将各学习器结合起来，得出最终预测结果。
• 集成学习的一般结构：

1. 同质集成(homogeneous)：学习器使用的算法都是相同类型，例如全使用决策树算法。单个学习器称为 ‘基学习器’ 或 ‘基学习算法’。
2. 异质集成(heterogenous)：学习器使用的算法类型不同，例如同时使用决策数、SVM等算法。单个学习器称为 ’ 组件学习器’。

• 集成学习的方法：

1. Bagging：学习器之间不存在强依赖关系，各学习器可独立并行。
2. Boosting：学习器之间存在强依赖关系，通常后一个学习器是对前一个学习器的补充。

• 集成学习效果强大尤其是针对弱学习器(即精度略高于50%算法模型)，虽然单个弱学习器效果很差，但是成百上千的弱学习器集成在一起，错误率以指数级下降，理论上可以趋于0。
  
  
  
  

Bagging

• 基本概念

1. 当想要集成成百上千的学习器时，学习器之间的差异就尤为重要(如果都一样就体现不出集成学习的效果)。虽然有很多机器学习算法，但是远远不够的，必须为每一种算法创建更多的子模型且子模型之间要有差异性。
2. 如何创建有差异的子模型？即在训练时，使用的数据保持差异。
   1. Pasting： 无放回抽取。假设500个训练数据，每次抽取100各样本，则同一算法只可训练出5个差异子模型，且随机性比较大。
   2. Bagging： 有放回抽取。同样500个训练数据，每次抽取100各样本，则同一算法可训练出成百上千的子模型，也能避免随机性问题。
      对于有放回的取样，假设m个样本，每次抽1个样本，抽m次，因此任意一个样本在m次抽取中始终沒被抽到的概率$(1-\frac{1}{m})^m$，当对m取极限即：$lim_{m->\infin}(1-\frac{1}{m})^m=\frac{1}{e}\approx0.368$ 。所以平均大概有37%的样本不会被抽取到，这些未被取到的样本被称为Out-of-bag。
      因此就可以直接使用Out-of-bag作为验证数据集。
   3. Random Subspaces： 针对样本特征进行随机有放回抽取，生成不同的子特征空间，同样可以训练出大量差异模型。
   4. Random Patches： 即进行样本随机抽取，又进行特征随机抽取。

• Scikit-learn中的Bagging

• API：sklearn.ensemble.BaggingClassifier
• scikit-learn实现的bagging是同质集成(homogeneous)。
• 主要参数：

参数名	含义
base_estimator	指定基学习器，若为空则使用决策树，默认 = None
n_estimators	基学习器的数量，默认 = 10
max_samples	训练集X中随机抽取样本数，用于训练每个基学习器。int，即为数量；float，为比例：max_samples * X.shape[0]。默认 = 1.0
max_features	样本中随机抽取的特征数，用于训练每个基学习器。int，即为数量；float，为比例：max_samples * X.shape[1]。默认 = 1.0
bootstrap	是否选择有放回的抽取样本(bagging)，如果是False，则选择不放回抽取(pasting)。默认=True。
bootstrap_features	是否启用有放回的抽取特征，如果是False，不启用。默认=False。
oob_score	是否用out-of-bag，作为验证集，默认=False。
n_jobs	使用运算核心数，默认：None(1), -1代表使用全部
verbose	训练资讯显示，默认：0，数字越大越详细
random_state	随机种子

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier

'X总样本,y总label;X_train训练样本,y_train训练label;X_test训练样本,y_test训练label;'

'有放回的抽取样本'
bagging_clf = BaggingClassifier(DecisionTreeClassifier(),n_estimators=500, max_samples=100,bootstrap=True)
bagging_clf.fit(X_train, y_train)
bagging_clf.score(X_test, y_test)

'有放回的抽取样本和特征'
bagging_clf = BaggingClassifier(DecisionTreeClassifier(),n_estimators=500, max_samples=100,bootstrap=True,
max_features=2, bootstrap_features=True)
bagging_clf.fit(X_train, y_train)
bagging_clf.score(X_test, y_test)

'有放回的抽取样本和特征,并使用out-of-bag作为验证集'
random_patches_clf=BaggingClassifier(DecisionTreeClassifier(),n_estimators=500, max_samples=100,bootstrap=True, oob_score=True,max_features=1, bootstrap_features=True)
random_patches_clf.fit(X, y)
# oob_score_ 查看out-of-bag作为验证集的准确率。
random_patches_clf.oob_score_

• 随机森林

• 集成学习中的bagging即将样本或者特征抽样训练子模型的集成学习方式。而在bagging这种集成学习方式中使用决策树作为基学习器(base estimators)，就称为随机森林。
• 在sklearn中同样也直接实现了两种随机森林，普通随机森林(RandomForestClassifier)和极度随机森林(ExtraTreesClassifier)，结合策略均采用平均而非投票。
• 值得一提的是二者均提供了bootstrap参数，控制是否启用有放回抽取，但是没有提供调整抽取数量的max_samples参数。
• ExtraTreesClassifier 极度体现在，在子特征集中选取最佳特征时，每个特征仅随机取一个阀值进行划分，然后选最佳。提供了非常强大的随机性，抑制了过拟合，但增多了bias(偏差)。
• 普通随机森林 API: sklearn.ensemble.RandomForestClassifier
• 主要参数： 基本为决策树和bagging参数集合

参数名	含义
n_estimators	森林里决策树的数量，默认 = 10
criterion	衡量算法： ‘gini’(默认)， ‘entropy’
min_samples_split	子节点拆分所需的最小样本数：如果是int，直接表示最小样本数，如果是float，表示概率，最小样本数为min_samples_split * n_samples。默认 = 2。
min_samples_leaf	子节点至少要有的样本数：如果是int，直接表示需要样本数，如果是float，表示概率，需要样本数为min_samples_split * n_samples。默认 = 1。
max_depth	树的最大深度。默认 = None，扩展节点直到所有子节点都是纯的或直到所有子节点包含少于min_samples_split样本。
max_leaf_nodes	最多能有多少子节点，默认=None，可以有无限个。
min_impurity_decrease	节点继续分裂的最小杂质含量，float，默认 = 0
max_features	每次拆分考虑的特征数量：int,float,‘auto’(默认),‘sqrt’,‘log2’,‘None’。None即考虑全部特征。
bootstrap	是否选择有放回的抽取样本，如果是False，则使用整个数据集。默认=True。
oob_score	是否用out-of-bag，作为验证集，默认=False。
class_weight	各类别的权重：字典({0:0.9,1:0.1})，‘balanced’，'balanced_subsample，默认None.

from sklearn.ensemble import RandomForestClassifier
rf_clf = RandomForestClassifier(n_estimators=500, oob_score=True, random_state=666, n_jobs=-1)
rf_clf.fit(X, y)
rf_clf.oob_score_

• 极度随机森林API：sklearn.ensemble.ExtraTreesClassifier
• 主要参数：RandomForestClassifier与唯一不同bootstrap 默认不为True为 False。

from sklearn.ensemble import ExtraTreesClassifier
et_clf = ExtraTreesClassifier(n_estimators=500, bootstrap=True, oob_score=True, random_state=666, n_jobs=-1)
et_clf.fit(X, y)
et_clf.oob_score_

Boosting

• 基本概念

1. 与Bagging独立的集成多个有差异的模型不同，Boosting同样集成多个模型，但是每个模型并不是独立的，都是在其它模型的基础上继续增强整体集成模型的性能。

2. Boosting有两种典型的方法：

   1. Ada Boosting
      使用同样的训练数据集，训练完一个模型后再用此模型去预测此数据集，预测效果不太好的数据加大权重再将此数据集用于训练下一个模型。因此每一个模型都对前一个模型的补充，最后再将所有子模型结合起来，如下图：
      

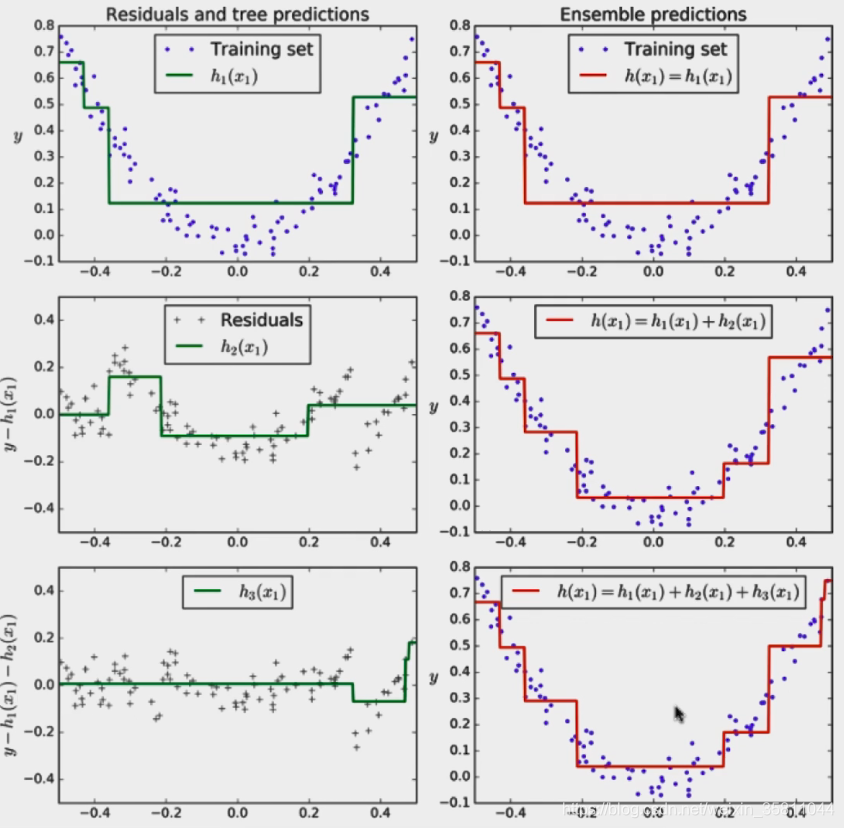
   2. Gradient Boosting
      使用同样的训练数据集，训练完一个模型后再用此模型去预测此数据集，预测效果不太好的数据取出再去训练一个新的模型，依次类推。因此每一个模型都是对前一个模型的修复，最后再将所有子模型加起来，如下图：

   
   

• Scikit-learn中的Boosting

• API：sklearn.ensemble.AdaBoostClassifier 和 sklearn.ensemble.GradientBoostingClassifier
• scikit-learn实现的boosting是同质集成(heterogenous)。

集成学习结合策略

• 对于分类任务，通常采用投票法结合各学习器预测结果。
• 投票法主要分为两种：Hard voting 和 Soft voting
• scikit-learn中封装了投票结合策略API：sklearn.ensemble.VotingClassifier 可用于结合多种学习器。
• 主要参数：

参数名	含义
estimators	元组列表，需用投票策略结合的学习器。
voting	投票方式：‘hard’(默认), ‘soft’。
weights	各类别投票所占权重，数组形式，shape (n_classifiers)，默认=None，权重统一。

1. Hard voting classifier
   1. 通过少数服从多数的形式，综合结果。

from sklearn.ensemble import VotingClassifier

'联合三种算法，采用少数服从多数。这里没有进行任何超参数的选择，应先找出每一种算法最佳结果的超参数，再集成起来进行判断。'
voting_clf = VotingClassifier (
	estimators=[
    ('log_clf', LogisticRegression()), 
    ('svm_clf', SVC()),
    ('dt_clf',  DecisionTreeClassifier())],
     voting='hard')

voting_clf.fit(X_train, y_train)
voting_clf.score(X_test, y_test)

2. Soft voting classifier
   1. 在某些情况下少数服从多数并不是合理的。
   2. 如下图：根据hard voting 样本将被分为B类，但是另外两个模型高度认定是A类而认为是B类的模型确认度并不高。
      
   3. 因此soft voting采用概率模型：
      A：(99% + 49% + 40% + 90% + 30%)/5 = 61.6%
      B：(1% + 51% + 60% + 10% + 70%)/5 = 38.4%
      结果应该定为A类。
   4. 因此，如果要使用soft voting投票方式，要求集成的分类算法必须支持概率输出的：
      逻辑回归：sigmoid函数就是概率。
      KNN：最近的几个点占总考虑点数的比重，可求出概率。
      决策树：与KNN类似，构建完成的树每一个子节点不一定都是纯的，gini或熵都不一定完全为0，因此每子节点都能根据里面不同类样本数(训练样本)算出该子节点属于某一类的概率。
      SVM：计算概率较为复杂，在scikit-learn中SVC里有一个参数 probability为true就可为SVM算法估计概率。

from sklearn.ensemble import VotingClassifier

'采用权重概率'
voting_clf2 = VotingClassifier(
	estimators=[
    ('log_clf', LogisticRegression()), 
    ('svm_clf', SVC(probability=True)),
    ('dt_clf', DecisionTreeClassifier(random_state=666))],
    voting='soft')
    
voting_clf2.fit(X_train, y_train)
voting_clf2.score(X_test, y_test)

集成学习回归问题

API：

• sklearn.ensemble.AdaBoostRegressor
• sklearn.ensemble.BaggingRegressor
• sklearn.ensemble.ExtraTreesRegressor
• sklearn.ensemble.GradientBoostingRegressor
• sklearn.ensemble.RandomForestRegressor
• sklearn.ensemble.VotingRegressor

这些类与之前用于分类的集成学习方法，用法几乎都是一致的，只不过最后返回的是一个具体的数字，用于解决回归问题。

来源：https://blog.csdn.net/weixin_35811044/article/details/100172344