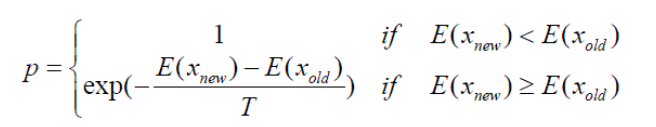这个算法是在《集体智慧编程》中读到的,页码大概是在P95,有兴趣的同学可以私下好好专研一番,我在这里就简单的抒写一些个人感受以及内容介绍吧。
首先呢,介绍一些类似的优化算法以及这些算法中的各种不足与优点吧:
一、随机搜索法:顾名思义,就是不断的给出随机解,然后在大量的解中找到最优的那个解。
优点:思路简单,代码好写
缺点:如果不是八核、32G、第九代i7等这样的配置,估计你得运行上个好几天才能求出一个好的解
二、爬山法:就是顺着一个相对来说好的解的方向进行不断的求出最优解
优点:相对比起随机搜索法,显的理智了不少缺点:容易得到局部最优解,也就是看上去好像是最好的,实际也是好的,但不代表全部中的最好
三、模拟退火算法(本文主讲):受物理学领域启发而来的一种优化算法(看起来就牛逼吧,高端!),也是由一个问题的随机解开始。它用一个变量来表示温度,这一温度开始时非常高,然后逐渐降低。每一次迭代期间,算法回随机选中题解中的某个数字,然后朝某个方向变化
优点:能介绍局部最优解,如果这三个算法按学历来排的话,这个应该是博士吧
缺点:额......."博士"的缺点,身为本科生暂时没想到。
好咯,嗑瓜子部份的内容也讲完了,接下来就再来个爆米花内容的节目呗,介绍一下算法原理咯?
这里我就简单的略写一下把,上面的介绍也讲了一部分原理,这里来点专业点的把。
公式来一个:
嗯,大概就是这样,简单给大家描述一下,也就是这个T一开始数值会高,也就可以避免前面说的局部最优解这个问题了,这个T对避免这个局部最优解十分重要!比如:刚开始这个解的相差很小,在爬山法中可能就不会往这个方向进行了,但是在退火算法中,它就不一定了,它也可能会接受这样的解,以此来避免后面的局部最优解这个问题。
接下来,代码走起:
def annealingoptimize(domain,costf,T=10000.0,cool=0.95,step=1):
vec=[float(random.randint(domain[i][0],domain[i][1])) for i in range(len(domain))]
while T>0.1:
#随机选择一个需要修改的值
i=random.randint(0,len(domain)-1)
#选择一个改变索引值的方向
dir=random.randint(-step,step)
#创建一个代表题解的新列表,改变其中一个值
vecb=vec[:]
vecb[i]+=dir
if vecb[i]<domain[i][0]:
vecb[i]=domain[i][0]
elif vecb[i]>domain[i][1]:
vecb[i]=domain[i][1]
#计算当前成本和新的成本
ea=costf(vec)
eb=costf(vecb)
#它是更好的解吗?或者是趋向最优解的可能的临界解吗?
if(eb<ea or random.random()<pow(math.e,-(eb-ea)/T)):
vec=vecb
#然后逐步降低温度值进行迭代
T=T*cool
return vec
这部份呢,这部份的算法灵魂最主要的就是 :
if(eb<ea or random.random()<pow(math.e,-(eb-ea)/T)) 这条代码了,大家有兴趣的再好好的琢磨琢磨呗。
有兴趣的也可以和我一起探讨一下更多更有趣的算法,等你来噢!
来源:CSDN
作者:灰熊不会灰
链接:https://blog.csdn.net/weixin_41886611/article/details/103241585