协方差矩阵

首先我们给你一个含有n个样本的集合，依次给出数理统计中的一些相关概念：

标准差和方差一般是用来描述一维数据的，但现实生活我们常常遇到含有多维数据的数据集，以考试成绩为例，若要统计多个学科的考试成绩，就要用协方差，协方差就是一种用来度量两个随机变量关系的统计量，其定义为：

来度量各个维度偏离其均值的程度，标准差可以这么来定义：

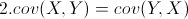
需要注意的是，协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算个协方差，那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

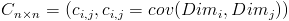
这个定义还是很容易理解的，我们可以举一个简单的三维的例子，假设数据集有三个维度，则协方差矩阵为

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。

上面涉及的内容都比较容易，协方差矩阵似乎也很简单，但实战起来就很容易让人迷茫了。必须要明确一点，协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。这个我将结合下面的例子说明，以下的演示将使用Matlab，为了说明计算原理，不直接调用Matlab的cov函数(蓝色部分为Matlab代码)。

首先，随机产生一个10*3维的整数矩阵作为样本集，10为样本的个数，3为样本的维数。

mysample = fix(rand(10,3)*50)

根据公式，计算协方差需要计算均值，那是按行计算均值还是按列呢。前面我们也特别强调了，协方差矩阵是计算不同维度间的协方差，要时刻牢记这一点。样本矩阵的每行是一个样本，每列为一个维度，所以我们要按列计算均值。为了描述方便，我们先将三个维度的数据分别赋值：

>> dim1 = mysample(:,1); >> dim2 = mysample(:,2); >> dim3 = mysample(:,3);

计算dim1与dim2，dim1与dim3，dim2与dim3的协方差：

>> sum((dim1 - mean(dim1)) .* (dim2 - mean(dim2))) / (size(mysample, 1) - 1)  %得到 -147.0667 >> sum((dim1 - mean(dim1)) .* (dim3 - mean(dim3))) / (size(mysample, 1) - 1)  %得到  -82.2667 >> sum((dim2 - mean(dim2)) .* (dim3 - mean(dim3))) / (size(mysample, 1) - 1)  %得到   76.5111

搞清楚了这个后面就容易多了，协方差矩阵的对角线就是各个维度上的方差，下面我们依次计算：

>> var(dim1)  %得到 227.8778 >> var(dim2)  %得到 179.8222 >> var(dim3)  %得到 156.7111

>> cov(mysample)

Update

但是通常我们不用上述方法，而是用下面简化的方法进行计算：

先让样本矩阵中心化，即每一维度减去该维度的均值，然后直接用新的到的样本矩阵乘上它的转置，然后除以(N-1)即可。其实这种方法也是由前面的公式通道而来，只不过理解起来不是很直观而已。大家可以自己写个小的矩阵看一下就明白了。其Matlab代码实现如下：

>> temp = mysample - repmat(mean(mysample), 10, 1);% 中心化样本矩阵 >> result = temp' * temp ./ (size(mysample, 1) - 1)

（为方便对matlab不太明白的人，小小说明一下各个函数，同样，对matlab有一定基础的人直接跳过：

B = mean(A)的说明：

如果你有这样一个矩阵：A = [1 2 3; 3 3 6; 4 6 8; 4 7 7];
用mean(A)（默认dim=1）就会求每一列的均值
ans =


ans =

如果在size函数的输入参数中再添加一项n，并用1或2为n赋值，则 size将返回矩阵的行数或列数。其中r=size(A,1)该语句返回的是矩阵A的行数， c=size(A,2) 该语句返回的是矩阵A的列数）

参考

https://blog.csdn.net/xiao_lxl/article/details/72730000

https://my.oschina.net/gujianhan/blog/225241

文章来源: 协方差矩阵