一.聚类(clustering)
1.k-均值聚类(k-means)
这是机器学习领域除了线性回归最简单的算法了。该算法用来对n维空间内的点根据欧式距离远近程度进行分类。
INPUT:
K(number of clusters)
OUTPUT:
K个聚类中心
算法工作原理摘要:

#簇数为k#数据空间维度为n#训练集元素数为mdef K_means_demo(k,n,m): clusters=np.random.randint(0,40,size=[k,n]) #随机生成聚类中心 tr_set=np.random.randint(0,40,size=[m,n]) #因为是模拟,所以自己随机生成的数据集for iter in range(0,5): clu_asist=np.zeros(shape=[k,n],dtype=int) for i in range(0,m): #遍历训练集内每个样本 min=9999999 owner=0 for j in range(0,k): #遍历所有聚心找到最近的聚心owner dis=0 for p in range(0,n): abso =tr_set[i][p] - clusters[j][p] dis+=abso*abso #dis为第i个元素和第j个聚心的欧式距离的平方 if dis-min < 0: min=dis owner=j for p in range(0,n): #渐进更新均值 clu_asist[owner][p]+=(tr_set[i][p]-clu_asist[owner][p])//(p+1) clusters=clu_asist return clusters
在上面的代码中我手动设定了迭代更新次数为5,因为我做的demo规模比较小,迭代几次便收敛了,而在实际使用中一般用( 迭代次数 || EarlyStop )作为迭代终止条件。
更新情况:(assume n=2,k=4,m=15)
(虽然我的demo不太显著,可毕竟是亲手做的QAQ)
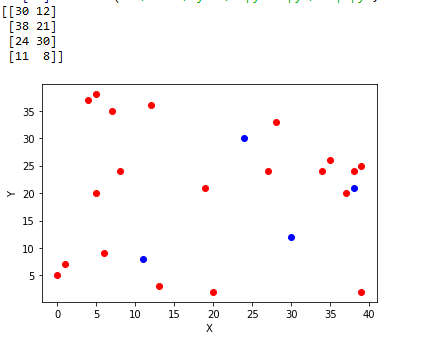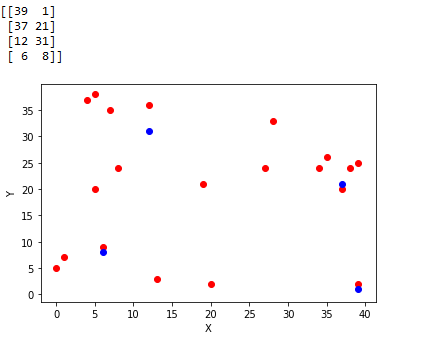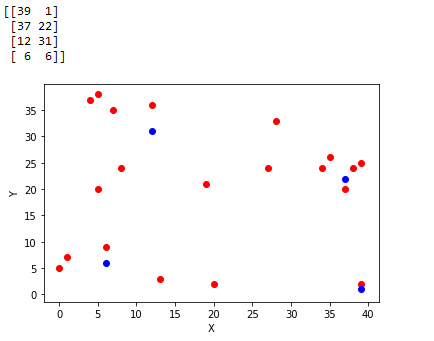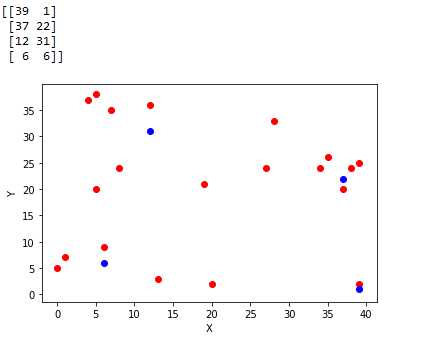
通读本算法,可以发现k-means对聚心初始值非常敏感,如果初始情况不好会震荡的。这里可以采取一些措施预判聚心大致要在哪个位置,然后直接将其初始化。
另外,关于收敛的判断,可以采取多种方法。比如使用代价函数
K-means优缺点分析:
只能发现球形类簇。
2.层次聚类(Hierarchical Clustering)
顾名思义,层次聚类就是一层一层地进行聚类。既可以由下向上对小的类别进行聚合(凝聚法),也可以由上向下对大的类别进行分割(分裂法)。在应用中,使用较多的是凝聚法。
INPUT:training_set D,聚类数目或者某个条件(一般是样本距离的阈值)
OUTPUT:聚类结果
凝聚法:
跟竞赛中经常出现的并查集问题略相似,凝聚法指的是先将每个样本当做一个类簇,然后依据某种规则合并这些初始的类簇,直到达到某种条件或者减少到设定的簇数。
在算法迭代中每次均选取类簇距离最小的两个类簇进行合并。关于类簇距离的计算表示方法主要有以下几种:
(1)取两个类中距离最小的两个样本的距离作为两个集合的距离
(2)取两个类中距离最大的两个样本的距离作为两个集合的距离
(3)计算两个集合中每两两点的距离并取平均值,这种方法要略费时
(4)比(3)轻松一些,取这些两两点距的中位数
(5)求每个集合中心点,然后以中心点代表集合来计算集合距离
(6)......
迭代会在簇数减少到设定数量时结束,当然,如果设定了阈值f,那么当存在两个距离小于f的集合时则会继续迭代直到不存在这样的两个集合。
分裂法:
首先将所有样本归类到一个簇,然后依据某种规则逐渐分裂,直到达到某种条件或者增加到设定的簇数。
(手写再拍照真不容易QAQ)

(1)K-means时间复杂度为O(N),而层次聚类时间复杂度为O(N^2),所以分层聚类不能很好地处理大批量数据,而k-means可以。
(2)K-means不允许嘈杂数据,而层次聚类可以直接使用嘈杂数据集进行聚类
(3)当聚类形状为超球形(如2D圆形,3D球形)时,k-means聚类效果更好。
3.基于密度聚类Mean Shift
4.基于密度聚类DBSCAN
5.高斯混合模型(GMM)与EM
6.基于图论聚类
二.降维(demensionality reduction)
1.主成分分析(PCA)
2.独立成分分析(ICA)
3奇异值分解(SVD)
4.t-SNE
来源:博客园
作者:dynmi
链接:https://www.cnblogs.com/dynmi/p/11619698.html