牛顿法,全称Newton's method。
当N=1时,
牛顿法的基本思想是:在现有极小点估计值的附近对f(x)做二阶泰勒展开,进而找到极小点的下一个估计值。设 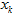 为当前的极小值点的估计值,那么通过二阶泰勒:
为当前的极小值点的估计值,那么通过二阶泰勒:

由于求的是最值, 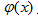 应满足
应满足
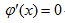
即

求得
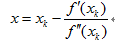
令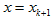 ,则
,则
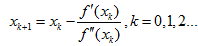
当N>1时,超过二维。二阶泰勒展开式可以做推广。
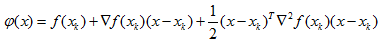
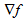 为f的梯度向量, 为f的海森矩阵,其定义如下所示。
为f的梯度向量, 为f的海森矩阵,其定义如下所示。
令
同理,
则
若矩阵非奇异,存在逆矩阵时,可求解为:
牛顿法算法伪代码:
缺点:原始牛顿法在迭代公式中没有步长因子,定 迭代,对于非二次型目标函数,有时会使函数值上升,表明牛顿法不能保证函数值稳定地下降,在严重的情况下,甚至可能造成迭代点列{ }发散而失败。
来源:博客园
作者:cymx66688
链接:https://www.cnblogs.com/cymx66688/p/11514568.html