OpenCV（四）之图像梯度处理

OpenCV（四）之图像梯度处理

• Gradient processing系列
• Gradient processing-Sobel算子
• Gradient processing-Scharr算子
• Gradient processing-Laplacian算子
• Gradient processing-计算梯度计算的对比

Gradient processing系列

在这一节中，我分析了关于图像梯度处理的几个方法，分析原理，代码实现，并观察有何差异。

---

Gradient processing-Sobel算子

	对于x-导数，或对y-导数进行转置。 	该函数通过将图像与适当的内核进行卷积来计算图像导数：

	Sobel算子结合了高斯平滑和微分，因此结果或多或少地抵抗噪声。  	大多数情况下，使用（xorder = 1，yorder = 0，ksize = 3）或（xorder = 0，yorder = 1，ksize = 3）， 	调用函数以计算第一个x或y图像导数。  	第一种情况对应于以下内核：

	第二种情况对应于以下内核：

	参数 	SRC	输入图像。 	DST	输出与src相同大小和相同通道数的图像。 	ddepth	输出图像深度，见#combinations ; 在8位输入图像的情况下，它将导致截断的导数。 	DX	导数x的顺序。 	DY	导数y的顺序。 	ksize	扩展的Sobel内核的大小; 它必须是1,3,5或7。 	scale	计算导数值的可选比例因子; 默认情况下，不应用缩放（有关详细信息，请参阅# getDerivKernels）。 	delta	在将结果存储在dst之前添加到结果中的可选delta值。 	borderType	像素外推法，参见#BorderTypes

---

function： def convertScaleAbs(src, dst=None, alpha=None, beta=None): 	缩放，计算绝对值，并将结果转换为8位。 	在输入数组的每个元素上，函数convertScaleAbs按顺序执行三个操作：缩放，取绝对值，转换为无符号8位类型：

$dst_i = saturate_{uchar}(|\alpha*src_i+\beta|)$

在多通道阵列的情况下，该功能独立处理每个通道。  当输出不是8位时，可以通过调用convertTo方法（或使用矩阵表达式）然后通过计算结果的绝对值来模拟操作。   	参数 	SRC	输入数组。 	DST	输出数组。 	alpha	可选的比例因子。 	beta	可选delta添加到缩放值。

Eg.

#导入图像 img = cv2.imread('car.png') 

#用sobel算子计算梯度，分别求X，Y方向的梯度 sobelX = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3) sobelY = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=3) #封装在plt中 plt.subplot(121) plt.imshow(sobelX) plt.title('sobelX') plt.subplot(122) plt.imshow(sobelY) plt.title('sobelY') #显示图片 plt.show() 

Result.1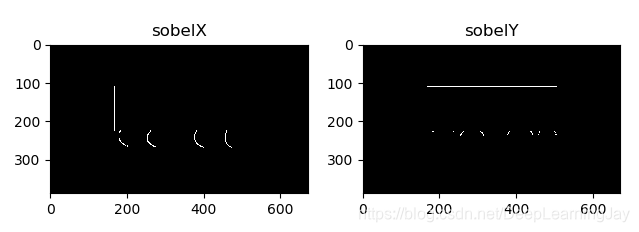

#白色到黑色的差值应该为正数，黑色到白色的差值，应该为负数，在sobel中所有的负数会被截断为0，所以要取绝对值 sobelX = cv2.convertScaleAbs(sobelX) sobelY = cv2.convertScaleAbs(sobelY) #分别计算x和y，再求和 sobelXY = cv2.addWeighted(sobelX,0.5,sobelY,0.5,0) cv_show('sobelXY',sobelXY) 

Result.2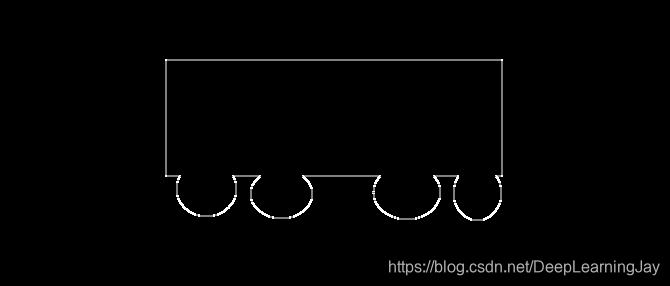

#如过直接在sobel函数中计算梯度，效果并不理想 # sobelXY = cv2.Sobel(img,cv2.CV_64F,1,1,ksize=3) # sobelXY = cv2.convertScaleAbs(sobelXY) # cv_show('sobelXY',sobelXY) 

Result.3

#使用其他图片测试,导入 lena = cv2.imread('lena.jpg',cv2.IMREAD_GRAYSCALE) #分别计算sobelX和sobelY lena_sobelX = cv2.Sobel(lena,cv2.CV_64F,1,0,ksize=3) lena_sobelY = cv2.Sobel(lena,cv2.CV_64F,0,1,ksize=3) #将其中负值都绝对值化 lena_sobelX = cv2.convertScaleAbs(lena_sobelX) lena_sobelY = cv2.convertScaleAbs(lena_sobelY) #将sobelX,Y融合 lena_sobelXY = cv2.addWeighted(lena_sobelX,0.5,lena_sobelY,0.5,0) #显示图像 res = np.hstack((lena,lena_sobelXY)) cv_show('lenas',res) 

Result.4

Note.

1.建议不直接通过sobel函数实现X和Y方向上的梯度运算，因为这样计算的结果通常不准确且会有重叠。

---

Gradient processing-Scharr算子

function： def Scharr(src, ddepth, dx, dy, dst=None, scale=None, delta=None, borderType=None): 	使用Scharr算子计算第一个x或y图像导数。 	该函数使用Scharr算子计算第一个x或y空间图像导数。 函数方法为：

相当于：

	参数 	SRC	输入图像。 	DST	输出与src相同大小和相同通道数的图像。 	ddepth	输出图像深度，请参阅#combinations 	DX	导数x的方向。 	DY	导数y的方向。 	scale	计算导数值的可选比例因子; 默认情况下，不应用缩放（有关详细信息，请参阅getDerivKernels）。 	delta	在将结果存储在dst之前添加到结果中的可选delta值。 	borderType	像素外推法，参见cv :: BorderTypes

Eg.

#与sobel算子相比，Scharr中的核中数值会大一点 #分别计算ScharrX和ScharrY lena_scharrX = cv2.Scharr(lena,cv2.CV_64F,1,0) lena_scharrY = cv2.Scharr(lena,cv2.CV_64F,0,1) #将其中负值都绝对值化 lena_scharrX = cv2.convertScaleAbs(lena_scharrX) lena_scharrY = cv2.convertScaleAbs(lena_scharrY) #将sobelX,Y融合 lena_scharrXY = cv2.addWeighted(lena_scharrX,0.5,lena_scharrY,0.5,0) #显示图像 res = np.hstack((lena,lena_scharrXY)) cv_show('lenas',res) 

Result.1

Note.

1.Scharr算子其实本质上应该与Sobel算子的原理一致，不过Scharr算子核中的数值会比Sobel算子的数值大，这将会使得，与锚点相近的像素点权重都变得更大，差异更大，也就能够把一些Sobel算子中没有计算出来的微小梯度放大。

---

Gradient processing-Laplacian算子

function： def Laplacian(src, ddepth, dst=None, ksize=None, scale=None, delta=None, borderType=None): 	计算图像的拉普拉斯算子。 	当ksize> 1时，该函数通过将使用Sobel运算符来计算X和Y的二阶导，进而相加来计算源图像的拉普拉斯算子：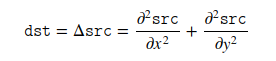

当ksize == 1时，通过使用以下3×3过滤器过滤图像来计算拉普拉斯算子：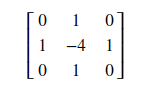

	参数 	SRC	来源图片。 	DST	与src相同大小和相同通道数的目标图像。 	ddepth	目标图像的所需深度。 	ksize	用于计算二阶导数滤波器的过滤器大小。有关详细信息，请参阅getDerivKernels。大小必须是正数且为奇数。 	scale	计算的拉普拉斯算子值的可选比例因子。默认情况下，不应用缩放。有关详细信息，请参阅getDerivKernels。 	delta	在将结果存储在dst之前添加到结果中的可选增量值。 	borderType	像素外推方法，请参阅cv :: BorderTypes

Eg.

#laplacian算子只需要调用一次，不必分别指定X，Y方向导数 lena_laplacian = cv2.Laplacian(lena,cv2.CV_64F) #将其中负值都绝对值化 lena_laplacian = cv2.convertScaleAbs(lena_laplacian) # #显示图像 res = np.hstack((lena,lena_laplacian)) cv_show('lenas',res) 

Result.1

Note.

1.laplacian算子是计算二阶导。

---

Gradient processing-计算梯度计算的对比

Code.

#显示原图以及各种算子计算梯度的效果图 res = np.hstack((lena,lena_sobelXY,lena_scharrXY,lena_laplacian)) cv_show("all",res) 

Result.

Note.

1.Sobel算子能大致计算出图像的梯度变化，Scharr算子计算较之更加细化，能把更细小的梯度变化计算出来。
2.Laplacian算子计算的梯度，略显模糊，但各个算子，应该都有在不同场合下必要的应用。

---

END

来源：51CTO

作者：DeepLearningJay

链接：https://blog.csdn.net/DeepLearningJay/article/details/100162915