常用的聚类方法:
①分裂方法:
K-Means算法(K-平均)、K-MEDOIDS算法(K-中心点)、CLARANS算法(基于选择的算法)
②层次分析方法:
BIRCH算法(平衡迭代规约和聚类)、CURE算法(代表点聚类)、CHAMELEON算法(动态模型)
③基于密度的方法:
DBSCAN(基于高密度连接区域)、DENCLUE算法(密度分布函数)、OPTICS算法(对象排序识别)
④基于网格的方法:
STING算法(统计信息网络)、CLIOUE算法(聚类高维空间)、WAVE-CLUSTRE(小波变换)
⑤基于模型的方法:
统计学方法、神经网络方法
其中Kmeans、K中心点、系统聚类比较常用。
KMeans:K-均值聚类也叫快速聚类法,在最小化误差函数的基础上将数据划分为预定的类数K。该算法原理简单并便于处理大量的数据。
K中心点:K-均值算法对孤立点的敏感性,K-中心点算法不采用簇中对象的平均值作为簇中心,而选用簇中离平均值最近的对象作为簇中心。
系统聚类:系统聚类也叫多层次聚类,分类的单位由高到低呈树形结构,且所处的位置越低,其所包含的对象就越少,但这些对象间的共同特征越多。该聚类方法只适合在小数据量的时候使用,数据量大的时候处理速度会非常慢。
KMeans聚类
K-Means:在最小化误差函数的基础上将数据划分为预定的类数K,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。
算法描述
①从N个样本数据中随机选取K个对象作为初始的聚类中心。
②分别计算每个样本到各个聚类中心的距离,将对象分配到距离最近的聚类中。
③所有对象分配完成后,重新计算K个聚类的中心。
④与前一次计算得到的K个聚类中心比较,如果聚类中心发生变化,转第②步。
⑤当质心不发生变化时停止并输出聚类结果。
聚类的结果可能依赖于初始聚类中心的随机选择,可能使得结果严重偏离全局最优分类。在实践中为了得到较好的结果,通常以不同的初始聚类中心,多次运行K-Means算法。在所有对象分配完成后,重新计算K个聚类的中心时,对于连续数据聚类中心取该簇的均值。
数据类型与属性度量
对于连续属性,要先对各属性值进行0-均值规范,再进行距离的计算。K-Means 聚类算法中,一般需要度量样本之间的距离、样本与簇之间的距离以及簇与簇之间的距离。
样本之间的相似性最常用的是欧几里得距离、曼哈顿距离和闵可夫斯基距离。
样本与簇之间的距离可以用样本到簇中心的距离$d\left(e_{i,}, x\right)$
簇与簇之间的距离可以用簇中心的距离$d\left(e_{i}, e_{j}\right)$
用p个属性来表示n个样本的数据矩阵:$$\left[\begin{array}{ccc}{x_{11}} & {\cdots} & {x_{1 p}} \\ {\vdots} & {} & {\vdots} \\ {x_{n 1}} & {\cdots} & {x_{n p}}\end{array}\right]$$
欧几里得距离的计算公式为:$$d(i, j)=\sqrt{\left(x_{i 1}-x_{j 1}\right)^{2}+\left(x_{i 2}-x_{j 2}\right)^{2}+\cdots+\left(x_{i p}-x_{j p}\right)^{2}}$$
曼哈顿距离的计算公式为:$$d(i, j)=\left|x_{i+}-x_{j 1}\right|+\left|x_{2}-x_{j 2}\right|+\cdots+\left|x_{i p}-x_{i p}\right|$$
闵可夫斯基距离的计算公式为:$$d(i, j)=\sqrt[q]{\left|\left(x_{i 1}-x_{j 1} |\right)^{q}+\left(\left|x_{i 2}-x_{j 2}\right|\right)^{q}+\cdots+\left(\left|x_{i p}-x_{j p}\right|\right)^{q}\right.}$$
q为正整数,q=1时为曼哈顿距离;q=2时为欧几里得距离。
对于文档数据,使用余弦相似性度量,先将文档数据整理成文档一词矩阵格式。
两个文档之间的相似度的计算公式为:$d(i, j)=\cos (i, j)=\frac{\vec{i} g \vec{j}}{|\vec{i}| g|\vec{j}|}$
目标函数
使用误差平方和SSE(残差平方和)作为度量聚类质量的目标函数,对于两种不同的聚类结果,可选择误差平方和较小的分类结果。
连续属性的SSE计算公式为:$$S S E=\sum_{i=1}^{K} \sum_{x \in E_{i}} \operatorname{dist}\left(e_{i,} x\right)^{2}$$
文档数据的SSE计算公式为:$$S S E=\sum_{i=1}^{K} \sum_{x \in E_{i}} \cos i n e\left(e_{i}, x\right)^{2}$$
簇$E_{i}$的聚类中心$e_{i}$的计算公式为:$$e_{i}=\frac{1}{n_{i}} \sum_{\dot{x} \in E_{i}} x$$
$K$表示聚类簇的个数,$E_{i}$表示第$i$个簇,$x$表示样本,$e_{i}$表示聚类中心,$n$表示数据集中样本的个数,$n_{i}$表示第$i$个簇中样本的个数。
例子
根据顾客的一些消费行为特性数据,将顾客进行聚类,并评价不同顾客群体的价值。
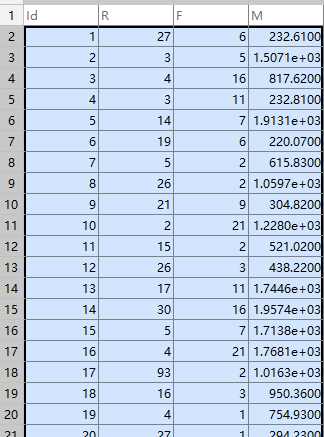
采用K-Means聚类算法,设定聚类个数K为3,最大迭代次数为500次,距离函数取欧氏距离。
%% 使用K-Means算法聚类消费行为特征数据 clear ; % 参数初始化 inputfile = '../data/consumption_data.xls'; % 销量及其他属性数据 k = 3; % 聚类的类别 iteration =500 ; % 聚类最大循环次数 distance = 'sqEuclidean'; % 距离函数 %% 读取数据 [num,txt]=xlsread(inputfile); data = num(:,2:end); %% 数据标准化 data = zscore(data); %% 调用kmeans算法 opts = statset('MaxIter',iteration); [IDX,C,~,D] = kmeans(data,k,'distance',distance,'Options',opts); %% 打印结果 for i=1:k disp(['第' num2str(i) '组聚类中心为:']); disp(C(i,:)); end disp('K-Means聚类算法完成!');
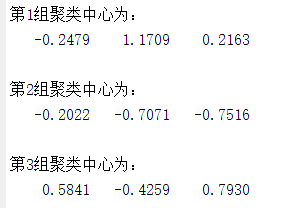
计算得到聚类中心为:
来源:博客园
作者:cruelty_angel
链接:https://www.cnblogs.com/fangxiaoqi/p/11459082.html