环境配置
BOOST下载boost_1_68_0x64
CGAL下载CGAL4.7x64
CMake下载x64 64位
VS2015 x64
1.编译boost
(1)打开命令行窗口;
(2)输入cmd.exe,回车;
(3)将boost根目录下面的booststrap.bat文件直接拖到cmd.exe打开的界面并回车,
(4)运行b2.exe;
(5)编译完成。
环境变量:
BOOST_LIBRARYDIR =...\boost_1_68_0x64\lib64-msvc-14.0
BOOST_ROOT = ...\boost_1_68_0x64
2.编译CGAL
(1)运行下载好的CGAL.exe。
(2)安装cmake,运行cmake-gui,进行设置:
(3)在cmake-gui界面点击左下角:Configure;
3.VS2015生成
(1) 打开CGAL.sln,在Debug和Release模式下都运行一遍。
(2) VS项目测试,新建控制台项目。添加x64配置。
多面体布尔运算流程
1.包含头文件,声明变量别名。
#include<CGAL/Exact_predicates_exact_constructions_kernel.h>
#include<CGAL/Polyhedron_3.h>
#include<CGAL/Nef_polyhedron_3.h>
#include<CGAL/Polyhedron_incremental_builder_3.h>
#include<CGAL/IO/Polyhedron_iostream.h>
typedefExact_predicates_exact_constructions_kernelKernel;
typedefPolyhedron_3<KernelPolyhedron;
typedefNef_polyhedron_3<Kernel> Nef_polyhedron;
typedefPolyhedron::HalfedgeDSHalfedgeDS;
typedefHalfedgeDS::VertexCGALVertex;
typedefCGALVertex::PointCGALPoint;
typedefPolyhedron::Point_iteratorPoint_iterator;
typedefPolyhedron::Facet_iteratorFacet_iterator;
typedefPolyhedron::Halfedge_around_facet_circulatorHalfedge_facet_circulator;
2.输入数据,mesh结构的多面体数据,包含一个顶点数组和一个多边形顶点索引的二维数组,该数组的一个存储单元表示一个简单多边形。
structVFMesh
std::vector<CGALPoint> pointlist;//点;
std::vector<std::vector<int>> facelist;//面,保存面的点的索引;
};
3.将输入的多面体数据转化为CGAL的多面体结构CGAL::Polyhedron_3<Kernel>(半边结构),Polyhedron的实现用到了灵活性很高的半边数据结构,要求多边形表面是二维可定向流形(orientable 2-manifolds)。按照CGAL的官方教程,可以新建一个模板类,实现数据的转换。
templateclassHDS>
classCgalPolyhedronpublicModifier_base<HDS>
{
public:
CgalPolyhedron(VFMeshmesh) : m_mesh(mesh) {}
voidoperator()(HDS& hds);
private:
VFMesh
};
最终的实现转换的函数接口为:(输入为mesh,输出为CGAL::Polyhedron)
voidVFMeshmesh, PolyhedronP);
4.CGAL中的Polyhedron并不能直接进行多面体的布尔运算,真正实现布尔运算的结构是CGAL::Nef_polyhedron_3<Kernel>(包含用于二元布尔运算所需要的结构信息),按照CGAL的官方教程,用Polyhedron来构造Nef_Polyhedron;Nef_Polyhedron重载了+,*,-运算符,分别表示并,交,差。
Polyhedron
Nef_polyhedron
Nef_polyhedron
Nef_polyhedron=+
布尔运算的结果仍为Nef_Polyhedron类型,调用Nef_Polyhedron的convert_to_polyhedron(Polyhedron)函数可以将Nef_Polyhedron转化回为Polyhedron。
out.convert_to_polyhedron(result);
然后通过接口函数 polyhedron2mesh将CGAL::Polyhedron_3<Kernel>转换为mesh。得到布尔运算的mesh结果:
voidVFMeshmesh, PolyhedronP);
5.CGAL中有独立的模型输入输出文件系统,模型文件的类型是.off文件。通过.off文件可以直接初始化CGAL::Polyhedron_3<Kernel>(重载了输出输入运算符),不再需要mesh结构进行初始化。
//生成 .off 文件
Polyhedron;
std::ifstream fin2("data\\input.off", std::ios::in);
fin2 >> polyhedron;
fin2.close();
//生成 .off 文件
std::ofstream"data\\result.off", std::ios::out);
fout <<polyhedron;
fout.close();
多面体布尔运算结果
输入数据


运算结果输出



| 输入:立方体 | 运算结果:交 | ||||
| 点集 | 1282 | 6146 | 189 | 502 | 510 |
| 面集 | 2560 | 6144 | 374 | 1000 | 1016 |
| 运行时间 | \ | \ | 3s | 4s | 4s |
1.在CGAL中点的坐标值类型为double,可以表示双精度的坐标点。
2.在进行布尔运算时,两个原始多面体的包含空间必须有交集。
3.CGAL::Polyhedron_3<Kernel>类型的多面体的每个面可以是多边形的结构,但是转换为CGAL::Nef_polyhedron_3<Kernel>时会自动三角化,所以最后的运算结果是三角面片构成的多面体。
4.多面体模型经过平移和旋转,只要两个多面体仍然坐标统一并有空间交集,就可以进行二元的布尔预算。
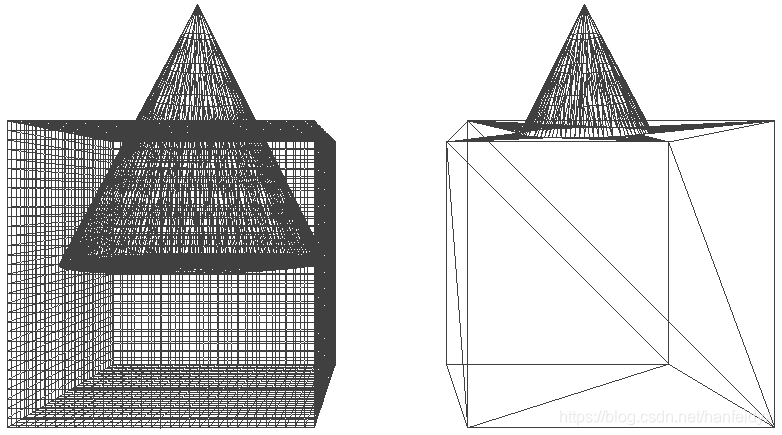
利用CGAL进行多面体的布尔运算可以保持很高的精度要求,无论是空间范围,还是坐标值的精度都可以满足常规的计算要求,但时间效率一般。
代码资源下载:https://download.csdn.net/download/hanfeidyx/10792922