假如deep learning得到不好的结果，应该从哪个方向进行改进呢？
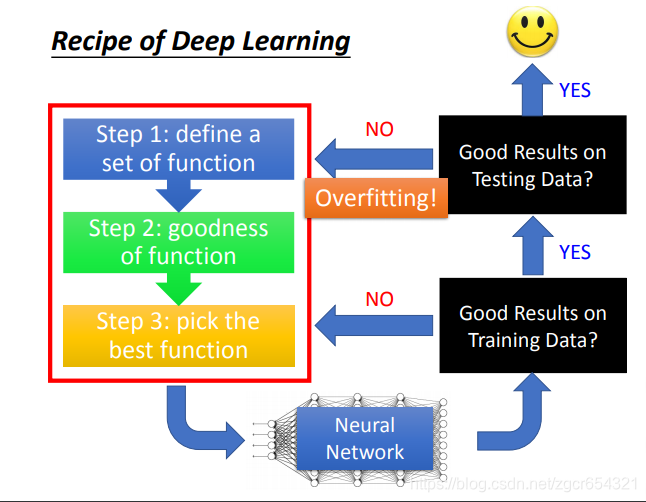
首先检查neural network在training data上是否得到好的结果。
如果在training data上得到好的结果，而在testing data上没有得到好的结果，那么这种情况就叫做overfitting。
如果在training data和testing data上都能得到好的结果，那么你就得到一个可以用的模型。
注意在神经网络层数不同时，层数更多的网络需要更多的训练次数才能训练好，如果比较两个层数不同的模型时，有时会发现一个层数少的模型的training error比层数多的模型还要下降的快，但这种情况有可能只是层数深的模型还没有训练好，需要更多训练次数。
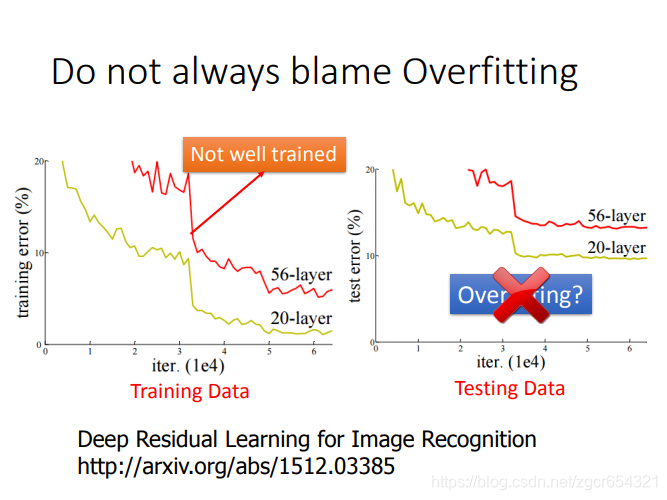
当然层数深的模型也不一定就比层数浅的模型表现要好。
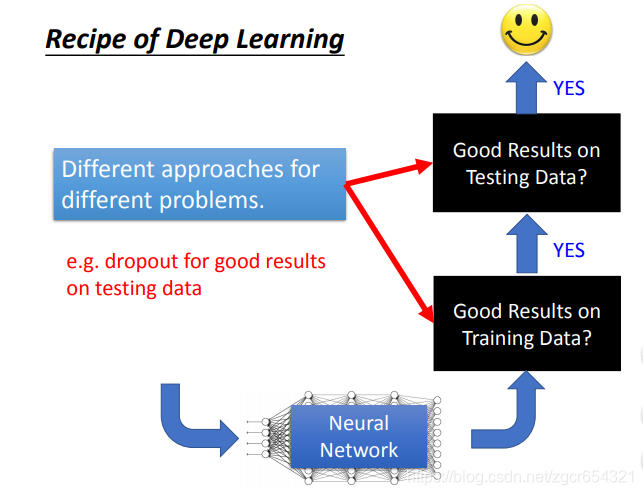
不同的方法应对不同的情况。有的是为了提升training set上的表现，而有的是提升testing set上的表现。
比如dropout是为了提升在testing set上的表现，而会使在training set上的表现变差。
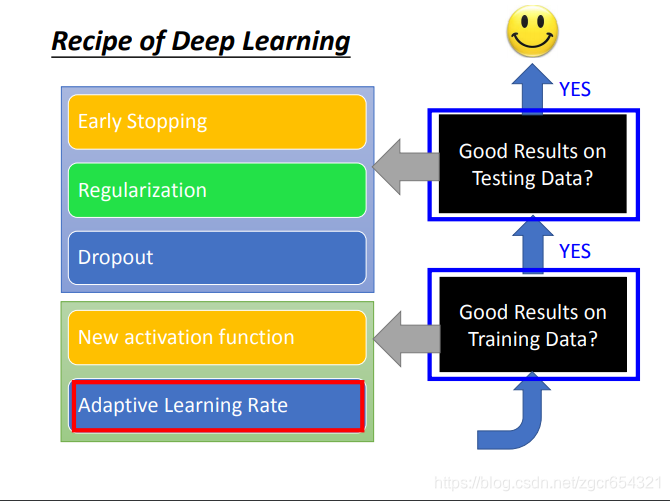
有哪些常用的方法：
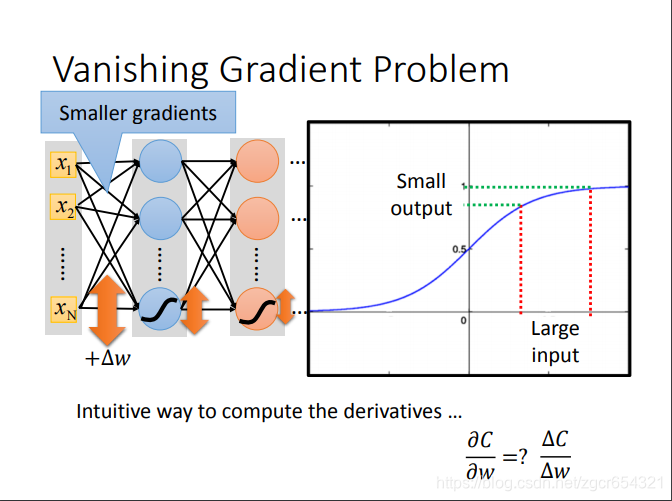
网络层数越深，表现不一定会更好。（梯度消失现象）梯度越小学习速度越慢。
梯度消失现象：由于反向传播的梯度是链式法则求导，最前面几层的学习率会越来越小，这样后面的loss到达local minima时，前面几层的权重还未学习到最合适的值。这也是激活函数从sigmoid函数改动relu函数的原因。
看sigmoid函数的特性：input变化很大时，output的变化相对来说并不大。
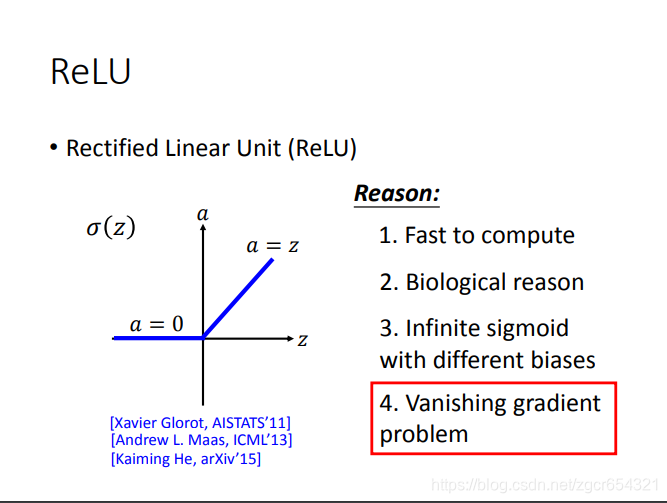
而relu函数则不会发生这样的情况，因为它的函数是下面这样的：
即输入值大于0，则输出等于输入值；输入值小于0，则输出值为0。
比如现在有一个两层的模型，都用relu作激活函数：
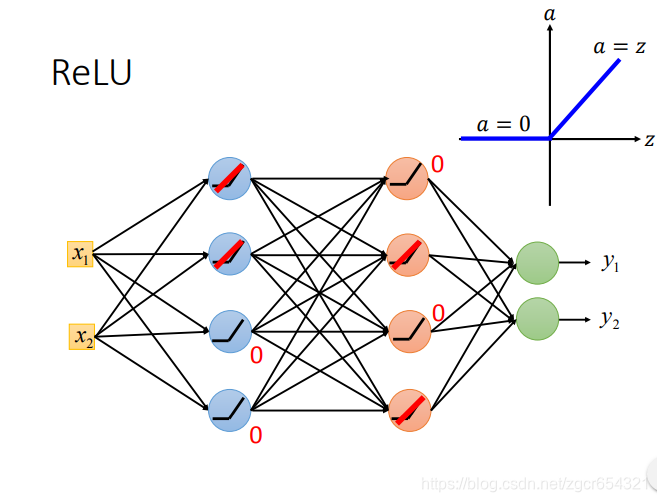
对于input大于0的神经元，这个神经元就相当于线性变换；对于input小于0的神经元，这个神经元的输出就是0，在反向传播的时候，计算这里参数的梯度是0，也就相当于不用更新。
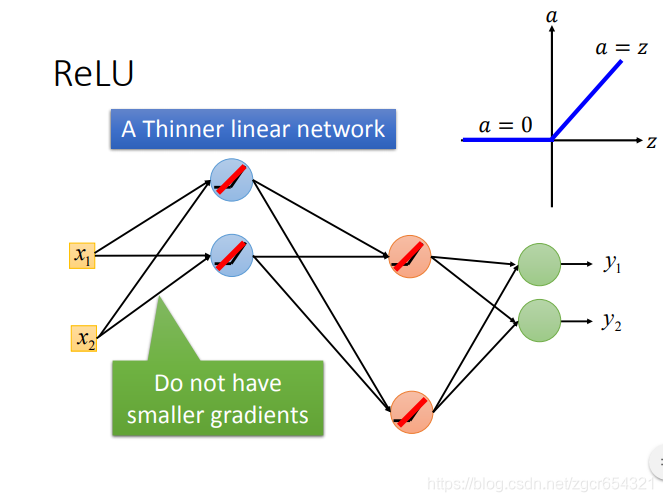
如果是线性的变换，那么就不会出现梯度消失的问题。这样这个模型中只有一部分神经元是线性的，而且不同层中作线性变换的神经元不一样，这样对于整个模型来说，模型就不是线性的，这样模型就可以模拟非线性的情况。
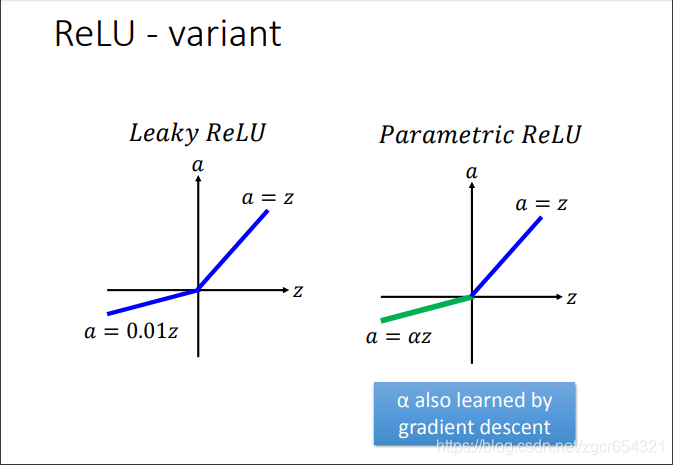
relu还有很多变形：
除此之外，还有之后提出来的ELU激活函数。
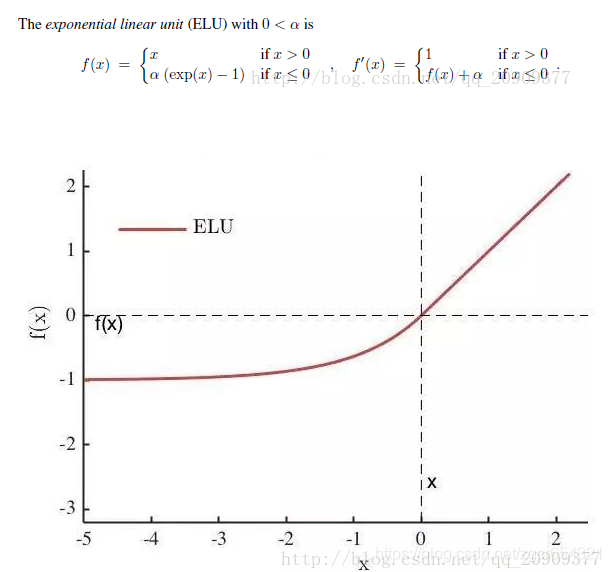
右侧线性部分使得ELU能够缓解梯度消失，而左侧软饱能够让ELU对输入变化或噪声更具有鲁棒性。
ELU的输出均值接近于零，所以收敛速度更快。
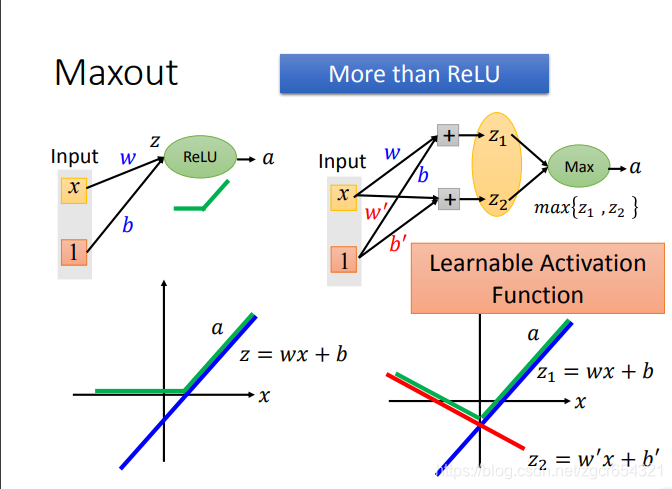
事实上，Relu是Maxout的一种特殊情况。
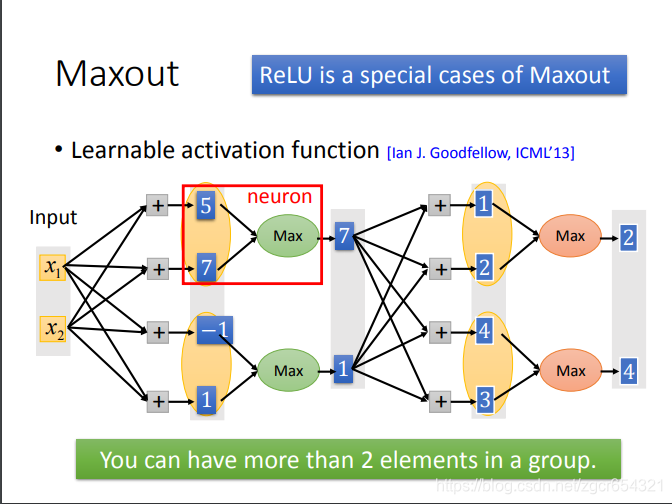
Maxout就是自动学习激活函数。模型可以自己学习每个神经元需要什么样的激活函数。
Maxout的原理：
比如上图x1和x2分别与4个神经元做运算，得到4个输出值，正常情况下，这4个输出值应该都要再经过激活函数的计算。
而在Maxout中是将这4个值分两组，第一组取其中最大值7，第二组取其中最大值1（有点像池化操作）。
后面一层的做法也类似。
为什么Maxout可以对不同的神经元产生不同的激活函数？
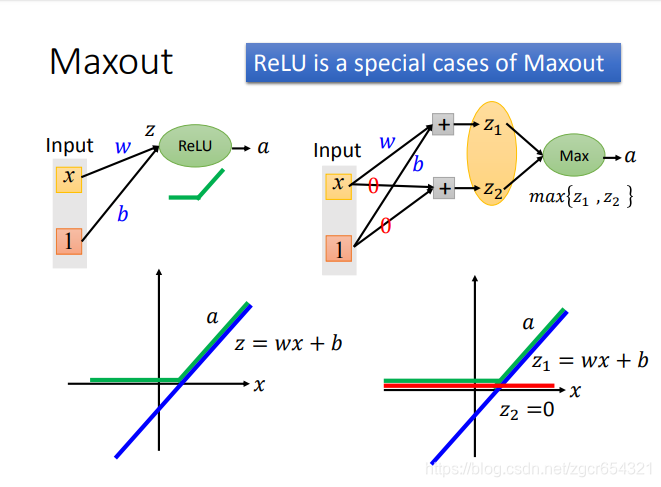
如果激活函数是relu时：
z=wx+b，是左图上的蓝色直线，是线性的。
而a是z经过relu处理的值，这时a就不是线性的了。
如果采用Maxout：
我们先计算出z1和z2，然后取max{z1,z2}。
我们可以看到z1和左图的蓝色直线一样，而z2是z2=0的直线。
这样我们可以发现通过max{z1,z2}所得的值在x的整个区间上就和relu函数得到的值一模一样了。
这就是用Maxout学习出来的激活函数就和relu函数一模一样了。对其他的激活函数也类似。
当然我们要注意Maxout学习出来的激活函数是分段的线性函数。
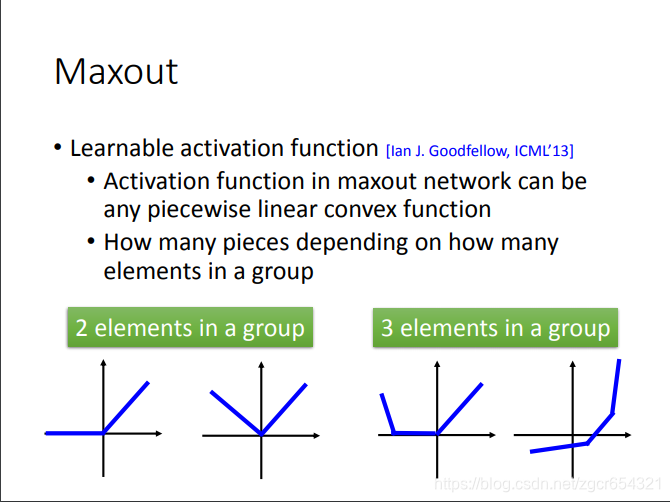
有多少段就取决于你的分组中有多少个神经元。
如何去train这个Maxout呢？
Maxout是可以train的。给定一组输入值x1和x2，我们假设红框是每个分组里的最大值，那么train参数时就将分组中其他较小的值当做不存在，这时我们就发现Maxout还是一个线性的函数，我们就可以用反向传播算法来更新每层的权重了。
而分组的其他值在其他不同的输入值时可能是最大值，故在其他不同的输入值时，它们也可以用反向传播算法来更新权重。
自适应学习率：
Adagrad的公式：
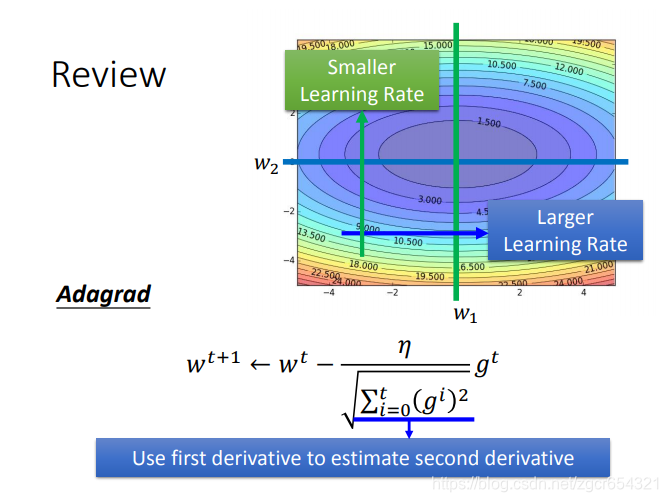
有时候我们需要不同的学习率。
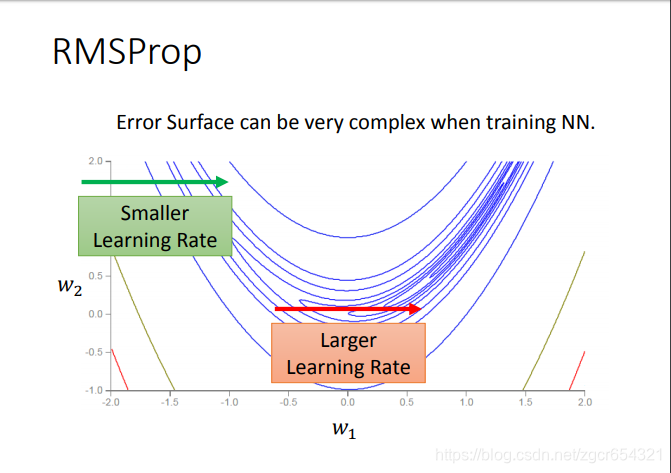
我们可以看到在w2值不同时需要的learning rate的大小不同。
这时候我们就要用RMSProp方法了。
RMSProp方法：
这个方法的核心就是在梯度越平坦的方向步子越大，梯度越陡峭的方向步子越小。
RMSProp与Adagrad的区别：
这是Adagrad：
这是RMSProp：
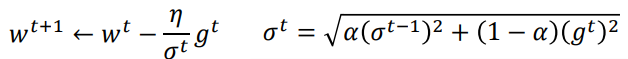
实际上就是分母由原来的所有步次的梯度和改为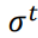
。（更多考虑上一步梯度的影响）
Momentum方法：
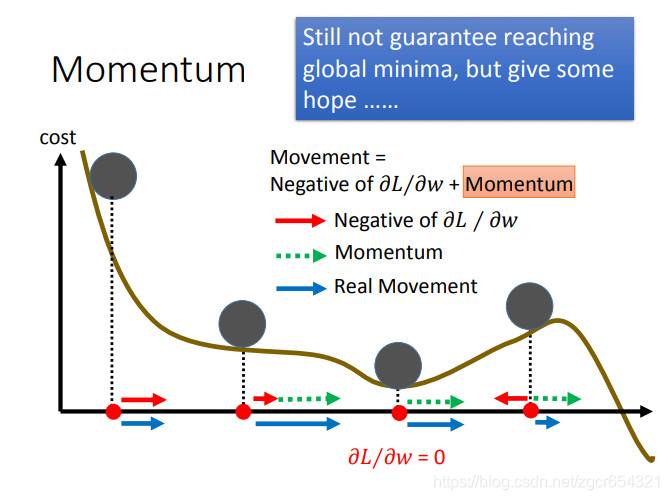
Momentum其实就是保留了上一步的梯度的跨步的幅度。
复习：一般的梯度下降方法：
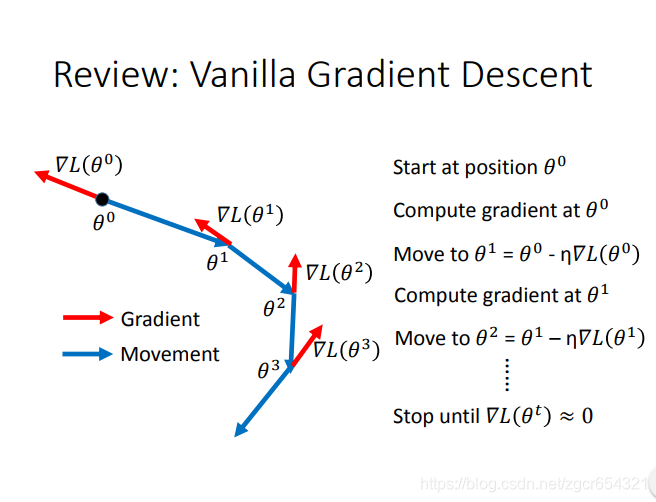
如果把RMSProp和Momentum的合并起来，就是Adam算法。
如何在testing data上也具有比较好的表现？
我们可以使用validation set来测试其testing error，这样可以及早在testing error升高前停下来。
实际应用时，就是train一段时间就用validation set来测试一下模型。
正则化也可以用来减少testing error。
如L2正则化：
其做梯度下降时：
加上正则项时，更新参数时，现在前面是
。前面括号内总是一次小于1的项，这样wt每次都会越来越小。
后面这项
会与前面这项取得平衡。
L1正则化：
dropout方法：
dropout就是丢掉一部分神经元的输出值。然后将剩下的输出值输入下一层。
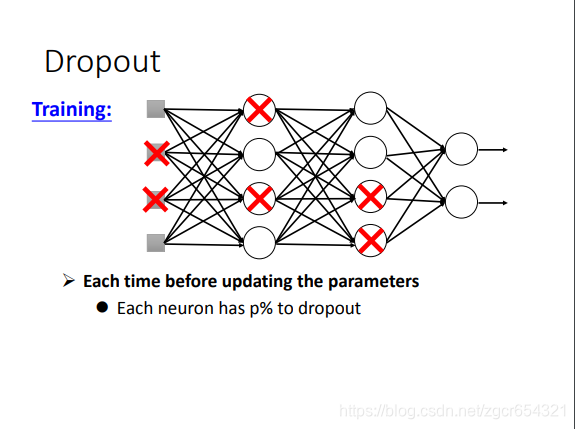
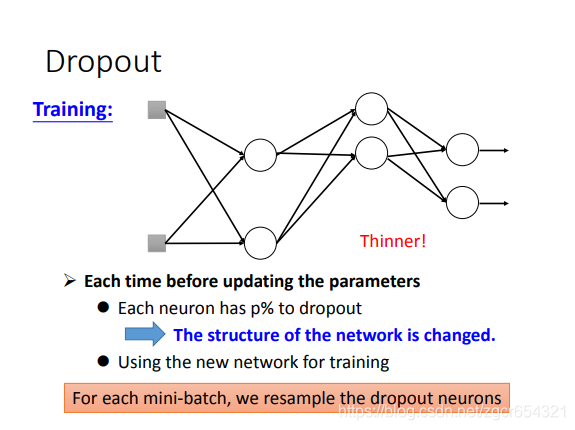
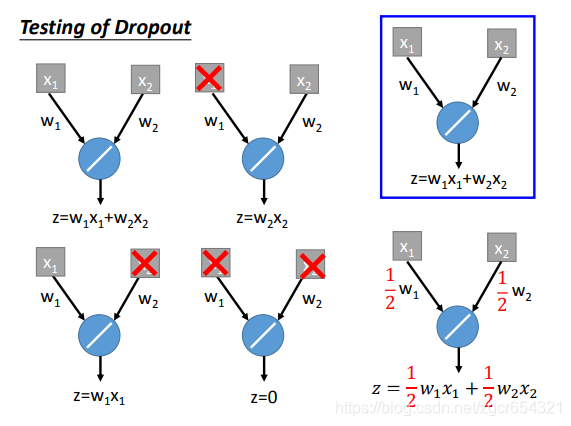
注意：
testing的时候是不dropout的。training时才dropout。
训练时多批样本会将所有神经元的权重都训练到，不需要担心训练不到的情况。
dropout可以看作是一种ensemble的方式。
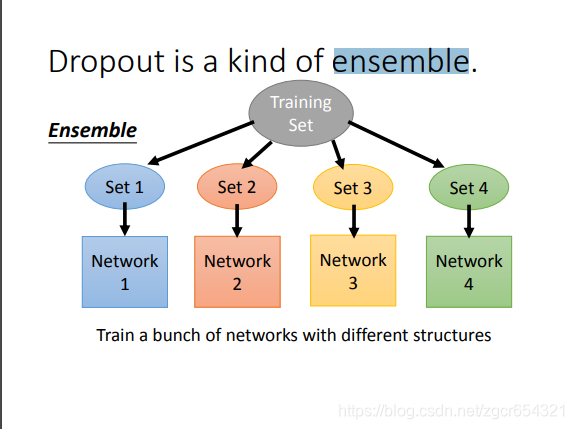
如果一个模型中有m个神经元，则经过dropout后可能产生2的m次方个的模型。
每一个模型都用一个minibath的样本去train它。注意它们的参数是共用的。所有的模型的参数拼起来就是完整的网络中的所有参数。
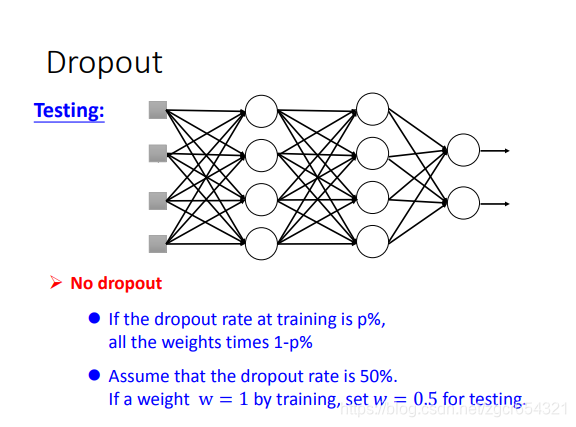
而在test时：
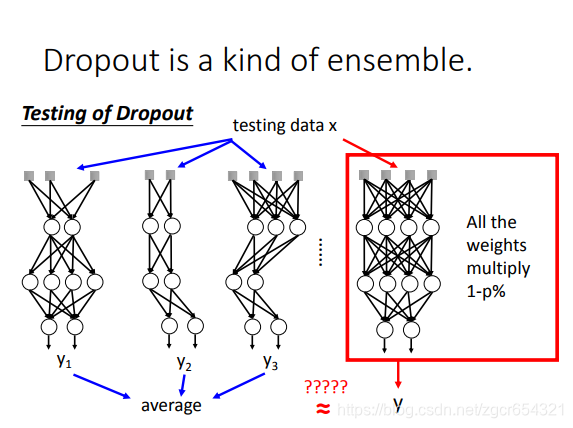
test时，所有的weights都乘以1-p%。
举例：
