买卖股票的最佳日期学会了动态规划

原创公众号：bigsai 欢迎加入力扣打卡
文章已收录在 全网都在关注的数据结构与算法学习仓库 欢迎star

祝大家新年快乐!万事如意!

买卖股票的最佳日期①

题目描述:

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 10^5
0 <= prices[i] <= 10^4

分析:
通过题意很容易知道题目的要求就是在整个数组中找到一个前后顺序差值最大的一对数字并将差值返回.如果使用暴力破解的方法(O(n2)向后遍历))固然可以但时间复杂度过高,所以我们就采取一个策略在O(n)的时间复杂度之内完成所有操作.

遍历的过程中需要借助一些变量来辅助记录一些操作,在这里我使用:

• int low:前面的最小值(初始为第一个元素),当然这个也可能会变动(遇到更小的会更新),记录前面已经枚举过的值中最小的作为买的日期.
• int value:用来记录结果,当然这是一个动态变化的过程,在枚举的过程记录前面的最小值,那枚举的值和前面最小值low的差如果大于value那么更新value.

在枚举途中(第一个元素可以不枚举)如果遇到下面两种情况需要做出处理:

• 枚举的值比最小值low还小,那么只需要更新这个low即可.
• 枚举的值和最小值的差大于value,那么更新value.

最后返回value即可.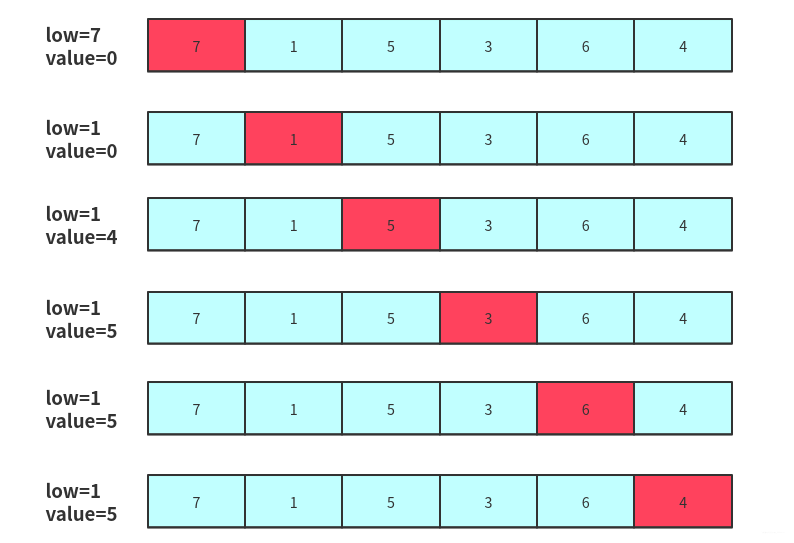

具体代码为:

class Solution {
   
   
   
    public int maxProfit(int[] prices) {
   
   
   
        if(prices.length<2)
            return  0;
        int value=0;
        int low=prices[0];
        for(int i=0;i<prices.length;i++)
        {
   
   
   
            if(prices[i]<low)
                low=prices[i];
            else if(prices[i]-low>value)
                value=prices[i]-low;
        }
        return  value;
    }
}

买卖股票的最佳日期②

题目描述:

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 3 * 10 ^ 4
0 <= prices[i] <= 10 ^ 4

分析:
这个该如何考虑呢?可以买的次数没有限制的.所以这个只要能买那就买(赚了就可买),还有一点比如序列1 3 5买1卖5转4,你可以看成买1卖3赚2,买3卖5赚2总共赚4,所以我们只需要找到相邻递增的差值叠加即是我们要找的值.

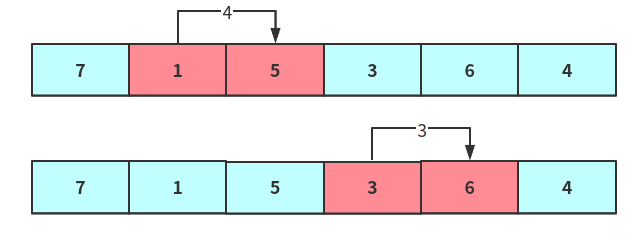
具体代码为:

class Solution {
   
   
   
    public int maxProfit(int[] prices) {
   
   
   
       if(prices.length<2)
            return  0;
        int value=0;
       
        for(int i=1;i<prices.length;i++)
        {
   
   
   
            if(prices[i]>prices[i-1])
                value+=prices[i]-prices[i-1];
        }
        return  value;
    }
}

买卖股票的最佳时机③

题目描述

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入：prices = [3,3,5,0,0,3,1,4]
输出：6
解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这个情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 10^5
0 <= prices[i] <= 10^5

分析
这个题和前面最大的不同就是最多只可以买卖两次.可能是一次或者两次.难度相比前面大一点,但是仔细思考还是很容易解决的,其实这题也不是很难,可以依靠动态规划的思想解决问题.

我们在上面第一题的时候用一个value保存当前一次的最大利润值,我们这题可以转化用用一个dpleft[]存储从左向右的最大结果,dpleft[i]表示0-i长度买卖一次的最大值. 所以我们只需要将整个数组拆分成两个部分看看,左侧的一个最大值,右侧的一个最大值.当然你可能会疑问那如果只买卖一次呢?那也很容易解决啊,只需要包含边界(其中一个长度为0就行啦).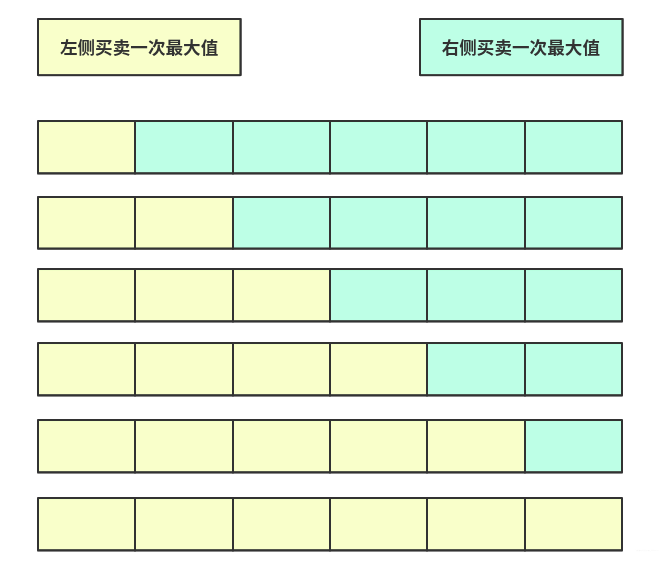

你可能会说那左侧右侧怎么算?从0号位置开始的很容易的得知计算方法和第一题相似,如果value最大值更新那么dp存这个值,否则dpleft[i]=dpleft[i-1]保留左侧值.

而右侧计算方法不需要从左向右再次计算,那样O(n2)的时间复杂度太慢了.对于右侧我们同样可以一次O(n)就可以解决,方法就是从右向左进行计算,和从左向右相反的是存储从右向左的最大值. dp的结果就是最大值和向前枚举的值的差.需要更新的时候就存储更新的值,否则dpright[i]=dpright[i+1];

最终

具体代码为:

class Solution {
   
   
   
    public int maxProfit(int[] prices) {
   
   
   
        int dpleft[]=new int[prices.length];//从左向右的
        int dpright[]=new int[prices.length+1];//多一个保留特殊情况
        if(prices.length<2)
            return  0;
        int value=0;//记录最大的那个
        int low=prices[0];
        for(int i=1;i<prices.length;i++)
        {
   
   
   
            dpleft[i]=dpleft[i-1];
            if(prices[i]<low) {
   
   
   
                low = prices[i];
            }
            else if(prices[i]-low>value) {
   
   
   
                value = prices[i] - low;
                dpleft[i] = value;
            }
        }
        int high=prices[prices.length-1];
        value=0;
        for(int i=prices.length-2;i>=0;i--)
        {
   
   
   
            dpright[i]=dpright[i+1];
            if(prices[i]>high)
            {
   
   
   
                high=prices[i];
            }
            else if(high-prices[i]>value)
            {
   
   
   
                value=high-prices[i];
                dpright[i]=value;
            }
        }

        value=0;//最终的结果
   
        for(int i=1;i<prices.length;i++)
        {
   
   
   
            int money=dpleft[i]+dpright[i];
            if(money>value)
                value=money;
        }
        return  value;
    }
}

原创不易，如果觉得有所收获，希望大家点赞、分享、在看一键三连帮忙扩散，谢谢！

咱们下次再见！关注后欢迎加入力扣打卡群(备注力扣 csdn即可)。

本文同步分享在 博客“Big sai”（CSDN）。
如有侵权，请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。

来源：oschina

链接：https://my.oschina.net/u/4160637/blog/4956957