1、单链表是否有环
题目描述:有一个单链表,其中可能有一个环,也就是某个节点的next指向的是链表中在它之前的节点,这样在链表的尾部形成一环。问题:
1、如何判断一个链表是不是这类链表?
2、如果链表为存在环,如何找到环的入口点?
一、判断链表是否存在环
设置两个指针(fast, slow),初始值都指向头,slow每次前进一步,fast每次前进二步,如果链表存在环,则fast必定先进入环,而slow后进入环,两个指针必定相遇。(当然,fast先行头到尾部为NULL,则为无环链表)。
1: boolean isExsitLoop() {
2: Node<T> slow = head;
3: Node<T> fast = head;
4:
5: while (fast != null && fast.next != null) {
6: slow = slow.next;
7: fast = fast.next.next;
8:
9: if (slow == fast)
10: return true;
11: }
12: return false;
13: }
二、找到环的入口点
当fast若与slow相遇时,slow肯定没有走遍历完链表,而fast已经在环内循环了n圈(1<=n)。假设slow走了s步,则fast走了2s步(fast步数还等于s 加上在环上多转的n圈),设环长为r,则:
2s = s + nr
s= nr
设整个链表长L,入口环与相遇点距离为x,起点到环入口点的距离为a。
a + x = nr
a + x = (n – 1)r +r = (n-1)r + L - a
a = (n-1)r + (L – a – x)
(L – a – x)为相遇点到环入口点的距离,由此可知,从链表头到环入口点等于(n-1)循环内环+相遇点到环入口点。于是我们从链表头、与相遇点分别设一个指针,每次各走一步,两个指针必定相遇,且相遇第一点为环入口点。
1: Node<T> getLoopEntry() {
2: Node<T> slow = head;
3: Node<T> fast = head;
4:
5: while (fast != null && fast.next != null) {
6: slow = slow.next;
7: fast = fast.next.next;
8:
9: if (slow == fast)
10: break;
11: }
12:
13: if (fast == null || fast.next == null)
14: return null;
15:
16: // slow指向链表头节点
17: // fast指向slow和fast相遇的节点
18: slow = head;
19:
20: while (slow != fast) {
21: slow = slow.next;
22: fast = fast.next;
23: }
24:
25: return fast;
26: }
2、两个链表是否相交
题目描述:给出两个单向链表的头指针(如下图所示),
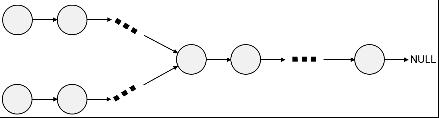
比如h1、h2,判断这两个链表是否相交。
直接循环判断第一个链表的每个节点是否在第二个链表中。但,这种方法的时间复杂度为O(Length(h1) * Length(h2))。显然,我们得找到一种更为有效的方法,至少不能是O(N^2)的复杂度。
- 针对第一个链表直接构造hash表,然后查询hash表,判断第二个链表的每个结点是否在hash表出现,如果所有的第二个链表的结点都能在hash表中找到,即说明第二个链表与第一个链表有相同的结点。时间复杂度为为线性:O(Length(h1) + Length(h2)),同时为了存储第一个链表的所有节点,空间复杂度为O(Length(h1))。是否还有更好的方法呢,既能够以线性时间复杂度解决问题,又能减少存储空间?
- 进一步考虑“如果两个没有环的链表相交于某一节点,那么在这个节点之后的所有节点都是两个链表共有的”这个特点,我们可以知道,如果它们相交,则最后一个节点一定是共有的。而我们很容易能得到链表的最后一个节点,所以这成了我们简化解法的一个主要突破口。那么,我们只要判断俩个链表的尾指针是否相等。相等,则链表相交;否则,链表不相交。
所以,先遍历第一个链表,记住最后一个节点。然后遍历第二个链表,到最后一个节点时和第一个链表的最后一个节点做比较,如果相同,则相交,否则,不相交。这样我们就得到了一个时间复杂度,它为O((Length(h1) + Length(h2)),而且只用了一个额外的指针来存储最后一个节点。这个方法时间复杂度为线性O(N),空间复杂度为O(1),显然比解法三更胜一筹。 - 上面的问题都是针对链表无环的,那么如果现在,链表是有环的呢?还能找到最后一个结点进行判断么?上面的方法还同样有效么?显然,这个问题的本质已经转化为判断链表是否有环。那么,如何来判断链表是否有环呢?
所以,事实上,这个判断两个链表是否相交的问题就转化成了:
1、先判断带不带环。
2、如果都不带环,就判断尾节点是否相等。
3、如果都带环,判断一链表上俩指针相遇的那个节点(问题1中的相遇节点),在不在另一条链表上。如果在,则相交,如果不在,则不相交。
这里为了简化问题,我们假设两个链表均不带环。
一、判断两链表链表是否有公共点
如果都不带环,就判断尾节点是否相等即可。如果都带环,判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
1: static boolean isCommonNode(LinkList<Integer> link, LinkList<Integer> link2) {
2: Node<Integer> last;
3: Node<Integer> last2;
4: // 两链表均无环
5: if (link.isExsitLoop() == false && link2.isExsitLoop() == false) {
6: // 获取最后一个节点
7: last = (Node<Integer>) link.getLastNode();
8: last2 = (Node<Integer>) link2.getLastNode();
9: System.out.println("链表1的最后一个节点为:"+last.value+" 链表2的最后一个节点为:"+last2.value);
10: return last.value == last2.value;
11: }
12: //一个有环,一个无环
13: else if(link.isExsitLoop()!=link2.isExsitLoop())
14: {
15: return false;
16: }
17: //两个都有环,判断环里的节点是否能到达另一个链表环里的节点
18: else
19: {
20: // 相遇节点
21: Node<Integer> meetNode = link.getMeetNode();
22: Node<Integer> meetNode2 = link2.getMeetNode();
23: Node<Integer> p = meetNode.next;
24:
25: // 环中遍历
26: while(p!=meetNode)
27: {
28: if(p == meetNode2)
29: return true;
30: p = p.next;
31: }
32: return false;
33: }
34: }
二、求两个链表相交的第一个节点
如果两个尾结点是一样的,说明它们有重合;否则两个链表没有公共的结点。 在上面的思路中,顺序遍历两个链表到尾结点的时候,我们不能保证在两个链表上同时到达尾结点。 这是因为两个链表不一定长度一样。但如果假设一个链表比另一个长L个结点,我们先在长的链表上遍历L个结点,之后再同步遍历,这个时候我们就能保证同时到达最后一个结点了。
由于两个链表从第一个公共结点开始到链表的尾结点,这一部分是重合的。因此,它们肯定也是同时到达第一公共结点的。于是在遍历中,第一个相同的结点就是第一个公共的结点。
1: static Node<Integer> getFirstCommonNode(LinkList<Integer> link, LinkList<Integer> link2)
2: {
3: Node<Integer> l = link.getHeadNode();
4: Node<Integer> s = link2.getHeadNode();
5: int len1 = link.getLength();
6: int len2 = link2.getLength();
7: int diff = len1 - len2;
8:
9: if(len1<len2)
10: {
11: l = link2.getHeadNode();
12: s = link.getHeadNode();
13: diff = len2 - len1;
14: }
15:
16: // 长的先走diff长度
17: for(int i = 0; i < diff; i++ )
18: l = l.next;
19:
20: while(l!=null&&s!=null&&l.value!=s.value)
21: {
22: l = l.next;
23: s = s.next;
24: }
25:
26: Node<Integer> comNode = null ;
27: if(l.value==s.value)
28: comNode = l;
29: return comNode;
30: }
具体代码为:
1: class Node<T> {
2: T value;
3: Node<T> next = null;
4:
5: public boolean equals(Node<T> node) {
6: if (value.equals(node.value)) {
7: return true;
8: }
9: return false;
10: }
11:
12: public int hashCode() {
13: return value.hashCode();
14: }
15:
16: public String toString() {
17: if (value == null)
18: return "-1";
19: return value.toString();
20: }
21: }
22:
23: class LinkList<T> {
24: private Node<T> head;
25: private int len;
26:
27: public LinkList() {
28: initLinkList();
29: }
30:
31: private void initLinkList() {
32: head = new Node<T>();// 空链表
33: len = 0;
34:
35: head.next = null;
36: }
37:
38: // 链表插入操作
39: void insertAfterHead(Node<T> node) {
40: node.next = head.next;
41: head.next = node;
42: len++;
43: }
44:
45: void insertAtLast(Node<T> node) {
46: Node<T> p = getLastNode();
47:
48: node.next = p.next; // null
49: p.next = node;
50: len++;
51:
52: }
53:
54: // 产生环
55: void insertFormLoop(Node<T> node) {
56: Node<T> p = getLastNode();
57:
58: node.next = p; // 产生环
59: p.next = node;
60: len++;
61: }
62:
63: Node<T> getHeadNode() {
64: return head;
65: }
66:
67: Node<T> getLastNode() {
68: Node<T> p = head;
69: // 获取最后一个节点
70: while (p.next != null) {
71: p = p.next;
72: }
73: return p;
74: }
75:
76: int getLength() {
77: return len;
78: }
79:
80: // 遍历
81: void traversal() {
82: Node<T> node = head.next;
83: while (node != null) {
84: System.out.print(node + "-->");
85: node = node.next;
86: }
87: System.out.println();
88: }
89:
90: /* http://www.cppblog.com/humanchao/archive/2008/04/17/47357.html
91: 设置两个指针(fast, slow),初始值都指向头,slow每次前进一步,fast每次前进二步,如果链表存在环,则fast必定先进入环,而slow后进入环,两个指针必定相遇。
92: (当然,fast先行头到尾部为NULL,则为无环链表)*/
93: // 判断是否有环
94: boolean isExsitLoop() {
95: Node<T> slow = head;
96: Node<T> fast = head;
97:
98: while (fast != null && fast.next != null) {
99: slow = slow.next;
100: fast = fast.next.next;
101:
102: if (slow == fast)
103: return true;
104: }
105: return false;
106: }
107:
108: // 有环的情况下,获取相遇节点
109: Node<T> getMeetNode()
110: {
111: Node<T> slow = head;
112: Node<T> fast = head;
113:
114: while (fast != null && fast.next != null) {
115: slow = slow.next;
116: fast = fast.next.next;
117:
118: if (slow == fast)
119: return slow;
120: }
121: return null;
122: }
123:
124: // 找出环的入口
125: /*
126: * 当fast若与slow相遇时,slow肯定没有走遍历完链表,而fast已经在环内循环了n圈(1<=n)。假设slow走了s步,则fast走了2s步(fast步数还等于s 加上在环上多转的n圈),设环长为r,则:
127: 2s = s + nr
128: s= nr
129: 设整个链表长L,入口环与相遇点距离为x,起点到环入口点的距离为a。
130: a + x = nr
131: a + x = (n – 1)r +r = (n-1)r + L - a
132: a = (n-1)r + (L – a – x)
133: (L – a – x)为相遇点到环入口点的距离,由此可知,从链表头到环入口点等于(n-1)循环内环+相遇点到环入口点,于是我们从链表头、与相遇点分别设一个指针,每次各走一步,两个指针必定相遇,且相遇第一点为环入口点。
134: * */
135: Node<T> getLoopEntry() {
136: Node<T> slow = head;
137: Node<T> fast = head;
138:
139: while (fast != null && fast.next != null) {
140: slow = slow.next;
141: fast = fast.next.next;
142:
143: if (slow == fast)
144: break;
145: }
146:
147: if (fast == null || fast.next == null)
148: return null;
149:
150: // slow指向链表头节点
151: // fast指向slow和fast相遇的节点
152: slow = head;
153:
154: while (slow != fast) {
155: slow = slow.next;
156: fast = fast.next;
157: }
158:
159: return fast;
160: }
161:
162: }
163:
164: public class LinkBasic {
165: // java内部类的初始化
166: class StaticInnerTest {
167: void innerClass() {
168: System.out.println("java内部类测试,innerClass");
169: }
170: }
171:
172: /* http://blog.csdn.net/v_JULY_v/article/details/6447013
173: 判断是否有公共点
174: 1、两个链表都无环的情况:判断尾节点是否相等
175: 2、如果都带环,判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
176: */
177: static boolean isCommonNode(LinkList<Integer> link, LinkList<Integer> link2) {
178: Node<Integer> last;
179: Node<Integer> last2;
180: // 两链表均无环
181: if (link.isExsitLoop() == false && link2.isExsitLoop() == false) {
182: // 获取最后一个节点
183: last = (Node<Integer>) link.getLastNode();
184: last2 = (Node<Integer>) link2.getLastNode();
185: System.out.println("链表1的最后一个节点为:"+last.value+" 链表2的最后一个节点为:"+last2.value);
186: return last.value == last2.value;
187: }
188: //一个有环,一个无环
189: else if(link.isExsitLoop()!=link2.isExsitLoop())
190: {
191: return false;
192: }
193: //两个都有环,判断环里的节点是否能到达另一个链表环里的节点
194: else
195: {
196: // 相遇节点
197: Node<Integer> meetNode = link.getMeetNode();
198: Node<Integer> meetNode2 = link2.getMeetNode();
199: Node<Integer> p = meetNode.next;
200:
201: // 环中遍历
202: while(p!=meetNode)
203: {
204: if(p == meetNode2)
205: return true;
206: p = p.next;
207: }
208: return false;
209: }
210: }
211:
212: // 求两个链表相交的第一个节点
213: /*
214: * 思路:如果两个尾结点是一样的,说明它们有重合;否则两个链表没有公共的结点。
215: 在上面的思路中,顺序遍历两个链表到尾结点的时候,我们不能保证在两个链表上同时到达尾结点。
216: 这是因为两个链表不一定长度一样。但如果假设一个链表比另一个长L个结点,我们先在长的链表上遍历L个结点,
217: 之后再同步遍历,这个时候我们就能保证同时到达最后一个结点了。
218: 由于两个链表从第一个公共结点开始到链表的尾结点,这一部分是重合的。因此,它们肯定也是同时到达第一公共结点的。
219: 于是在遍历中,第一个相同的结点就是第一个公共的结点。
220: * */
221:
222: static Node<Integer> getFirstCommonNode(LinkList<Integer> link, LinkList<Integer> link2)
223: {
224: Node<Integer> l = link.getHeadNode();
225: Node<Integer> s = link2.getHeadNode();
226: int len1 = link.getLength();
227: int len2 = link2.getLength();
228: int diff = len1 - len2;
229:
230: if(len1<len2)
231: {
232: l = link2.getHeadNode();
233: s = link.getHeadNode();
234: diff = len2 - len1;
235: }
236:
237: // 长的先走diff长度
238: for(int i = 0; i < diff; i++ )
239: l = l.next;
240:
241: while(l!=null&&s!=null&&l.value!=s.value)
242: {
243: l = l.next;
244: s = s.next;
245: }
246:
247: Node<Integer> comNode = null ;
248: if(l.value==s.value)
249: comNode = l;
250: return comNode;
251: }
252:
253: /**
254: * @param args
255: */
256: public static void main(String[] args) {
257: // TODO Auto-generated method stub
258: LinkBasic.StaticInnerTest test = new LinkBasic().new StaticInnerTest();
259: test.innerClass();
260:
261: /************************
262: * 形成初始单链表
263: * **********************/
264: LinkList<Integer> link = new LinkList<Integer>();
265: LinkList<Integer> link2 = new LinkList<Integer>();
266: int[] arr = { 1, 2, 3, 4, 5, 6 };
267: int[] arr2 = { 7, 1, 2, 3, 6, 8, 9, 10 };
268: for (int i = 0; i < arr.length; i++) {
269: Node<Integer> node = new Node<Integer>();
270: node.value = arr[i];
271: link.insertAfterHead(node);
272: }
273:
274: for (int i = 0; i < arr2.length; i++) {
275: Node<Integer> node = new Node<Integer>();
276: node.value = arr2[i];
277: link2.insertAfterHead(node);
278: }
279:
280: /************************
281: * 在链表尾部插入新的结点
282: * **********************/
283: Node<Integer> node = new Node<Integer>();
284: node.value = 7;
285: link.insertAtLast(node);
286:
287: System.out.println("链表1长度:" + link.getLength());
288: System.out.println("链表1表头信息:" + link.getHeadNode().value);
289: System.out.println("链表1遍历结果:");
290: link.traversal();
291:
292: System.out.println("链表2长度:" + link2.getLength());
293: System.out.println("链表2遍历结果:");
294: link2.traversal();
295:
296: /************************
297: * 判断两个链表是否有公共节点
298: * **********************/
299: System.out.println("是否存在公共节点:"+isCommonNode(link,link2));
300: System.out.println("第一个公共节点为:"+getFirstCommonNode(link,link2).value);
301:
302: /************************
303: * 在链表尾部插入结点,形成环
304: *
305: * 即在链表的最后一个元素p后插入节点node,使node的next指针域指向p,形成环结构
306: * **********************/
307: Node<Integer> node2 = new Node<Integer>();
308: node2.value = 19;
309: link.insertFormLoop(node2);
310: if (link.isExsitLoop()) {
311: System.out.println("单链表存在环。");
312: System.out.println("环的入口节点:" + link.getLoopEntry().value);
313: }
314:
315: }
316:
317: }
参考资料:
1、《编程之美》
来源:https://www.cnblogs.com/ttltry-air/archive/2012/08/14/2638284.html