[学习笔记] 连续Hopfield网络解TSP问题

连续Hopfield网络解TSP问题

上篇讲的是离散型Hopfield网络用于联想记忆，这篇接上篇讲利用连续型Hopfield网络解TSP问题。

模型

连续型Hopfield网络与离散型Hopfield网络结构是一致的，唯一区别就是节点取值连续和在时间上也连续。

连续型的Hopfield网络一般用一个电路图来研究：

这里感谢周启航同学对我在电路方面的指导，才让我看懂了他认为很简单的这么个图。

这是一组放大器电路的结构，神经元的激活函数由运算放大器来模拟，电压\(u_i\)为激活函数的输入，所并联的电阻R决定的是各个神经元之间的连接强度，R和电容C模拟神经元输出的时间常数，而电流I模拟的是阈值,w模拟神经元间的突触特性。

由这个电路图可以得到一组动态方程：
\[ C_j\frac{dU_j(t)}{dt} = \sum_i w_{ij}V_i(t) - \frac{U_j(t)}{R_j} + I_j \\V_j(t) = g_j(U_j(t)) \]
上面的方程描述的其实是一段时间内的电荷关系，这个很容易看出来，第二个方程描述的是激活函数g。这里用的是sigmoid函数。

其中w对应的是网络的权重，V是激活后的节点值，U是激活前的节点值。

优化目标

针对TSP问题，其目标函数为最小化能量函数E：
\[ E = \frac{A}{2}\sum_i \sum_j \sum_kV_{ij}V_{ik} \\ + \frac{B}{2}\sum_i \sum_j \sum_k V_{ji} V_{ki} \\ + \frac{C}{2} (\sum_i\sum_jV_{ij} - N)^2 \\ +\frac{D}{2} \sum_i\sum_j\sum_k W_{ij} V_{ik}(V_{j,k+1} + V_{j,k-1}) \]

其中V为节点值，\(V_{ij}\)代表第i个城市的的访问顺序，\(V_i\)是个one-hot向量。W是任意两城市间的距离矩阵，A、B、C、D是超参。

第一行的条件使得对任意第i行的元素其所在行的任意两元素相乘求和最小，最好的情况是最多只有一个非0元，第二行同理。

第三行使得所有元求和接近N。

第四行是所有路径求和的表达式，其中需要注意的是k+1如果大于节点数则取1，k-1如果小与1则取N(如果index从1开始的话)。那这个公式咋理解呢？i和j表示第i个和第j个城市，那如果i到j走的话，一定有个k使得\(V_{ik}\)为1，第i行的其他元为0，就意味着j的访问顺序要么是在i之前，要么在其之后，所以考虑k+1和k-1。

在“Theories on the Hopfield neural networks”这篇论文中对上式又进行了改进，提高了收敛速度。

其改进后的公式为目标函数为：
\[ E = \frac{A}{2}\sum_i(\sum_j V_{ij} -1)^2 + \frac{A}{2}\sum_j(\sum_i V_{ij} -1)^2 + \frac{D}{2}\sum_i\sum_j\sum_kW_{ij}V_{ik}V_{j,k+1} \]
改进后的公式更易于理解。前两项是保证每行每列只有一个1，最后一项是路程。

优化过程

由于在初始化阶段我们就能确定网络的权重，即任意两城市之间的距离，也就是权重不需要学习直接可以初始化。那么优化过程更新的其实是节点，我们先将节点按照如下规则进行初始化：
\[ U_{ij} = \frac{1}{2}U_0 ln(N-1)+ \delta_{ij} \]
其中\(\delta_{ij}\)为-1到+1的随机值。\(U_0\)为超参。

然后就是怎么取更新节点了。

节点的更新需要利用下面的公式：
\[ \frac{dU_{ij}}{dt} = - \frac{\partial E}{\partial V_{ij}} \]
其实对于电压对时间微分为啥等于右边我也不是很清楚，很多论文直接搬上来的，我无法解释，所以也直接搬过来。

带入能量定义式：
\[ \frac{dU_{ij}}{dt} = - \frac{\partial E}{\partial V_{ij}} = -A(\sum_kV_{ik}-1) - A(\sum_kV_{kj}-1) - D\sum_kd_{ik}V_{k,j+1} \]
然后更新节点：
\[ U_{ij}(t+1) = U_{ij}(t) + \frac{dU_{ij}}{dt} \Delta t \]
然后sigmoid激活：
\[ V_{ij} = \frac{1}{2}(1+ tanh(\frac{U_{ij}}{U_0})) \]

Coding

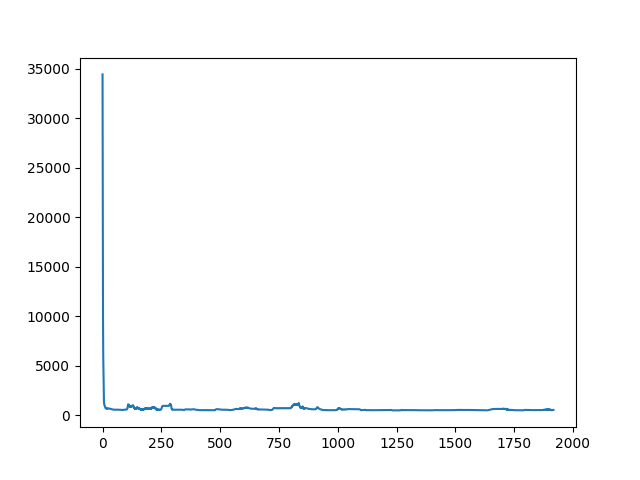
能量变化：

import numpy as np
import matplotlib.pyplot as plt 
class HopfieldTSPSolver():
    def __init__(self,cities):
        self.cities = cities
        self.n = cities.shape[0]
        self.u0 = 0.02
        self.delta_t = 1e-4
        self.A = 200
        self.D = 100
        self.W = np.zeros((self.n,self.n))
        self.U = np.zeros((self.n,self.n))
        self.V = np.zeros((self.n,self.n))
        self.init_weight()
        self.init_node()
    def init_weight(self,):
        for i in range(self.n):
            for j in range(self.n):
                self.W[i,j] = np.sqrt(np.sum((self.cities[i] - self.cities[j])**2))
    def init_node(self):
        for i in range(self.n):
            for j in range(self.n):
                self.U[i,j] = 0.5 * self.u0 * np.log(self.n-1) + np.random.random() * 2-1
    
    def diff(self,i,j):
        t = j+1 if j+1 < self.n else 0
        return -self.A*(np.sum(self.V[i]) -1) - self.A*(np.sum(self.V[:,j]) -1) - self.D * self.W[i,:].dot(self.V[:,t])    
    def get_energy(self):
        energy = 0.
        for i in range(self.n):
            energy += 0.5 * self.A * (np.sum(self.V[i,:]) - 1)**2
            energy += 0.5 * self.A * (np.sum(self.V[:,i]) - 1)**2
            for j in range(self.n):
                for k in range(self.n):
                    t = k+1 if k+1 < self.n else 0
                    energy += 0.5 * self.D * self.W[i,j] * self.V[i,k] * self.V[j,t]
        return energy
    def check(self):
        pos = np.where(self.V<0.2,0,1)
        flag = True
        if np.sum(pos) != self.n:
            flag = False
        for i in range(self.n):
            if np.sum(pos[:,i]) != 1:
                flag = False
            if np.sum(pos[i,:]) != 1:
                flag = False
        return flag
    def __call__(self):
        running_energy = []
        iter = 0
        while not self.check():
            iter +=1
            for i in range(self.n):
                for j in range(self.n):
                    self.U[i,j] += self.delta_t * self.diff(i,j)
            self.V = 0.5 * (1 + np.tanh(self.U / self.u0))
            energy = self.get_energy()
            running_energy.append(energy)
        return running_energy,np.where(self.V<0.2,0,1),iter
if __name__ == "__main__":
    cities = np.array([[2,6],[2,4],[1,3],[4,6],[5,5],[4,4],[6,4],[3,2]])
    solver = HopfieldTSPSolver(cities)
    energy,answer,iter = solver()
    print(answer)
    print(iter)
    plt.plot(energy)
    
    plt.show()
    

输出：

[[0 0 1 0 0 0 0 0]
 [1 0 0 0 0 0 0 0]
 [0 1 0 0 0 0 0 0]
 [0 0 0 1 0 0 0 0]
 [0 0 0 0 0 1 0 0]
 [0 0 0 0 1 0 0 0]
 [0 0 0 0 0 0 1 0]
 [0 0 0 0 0 0 0 1]]

1918

来源：https://www.cnblogs.com/aoru45/p/12482896.html