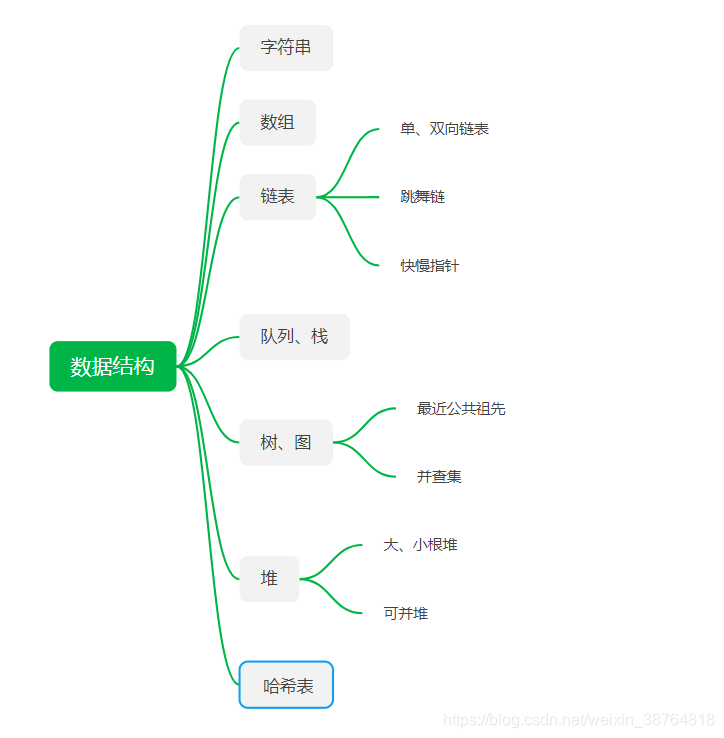
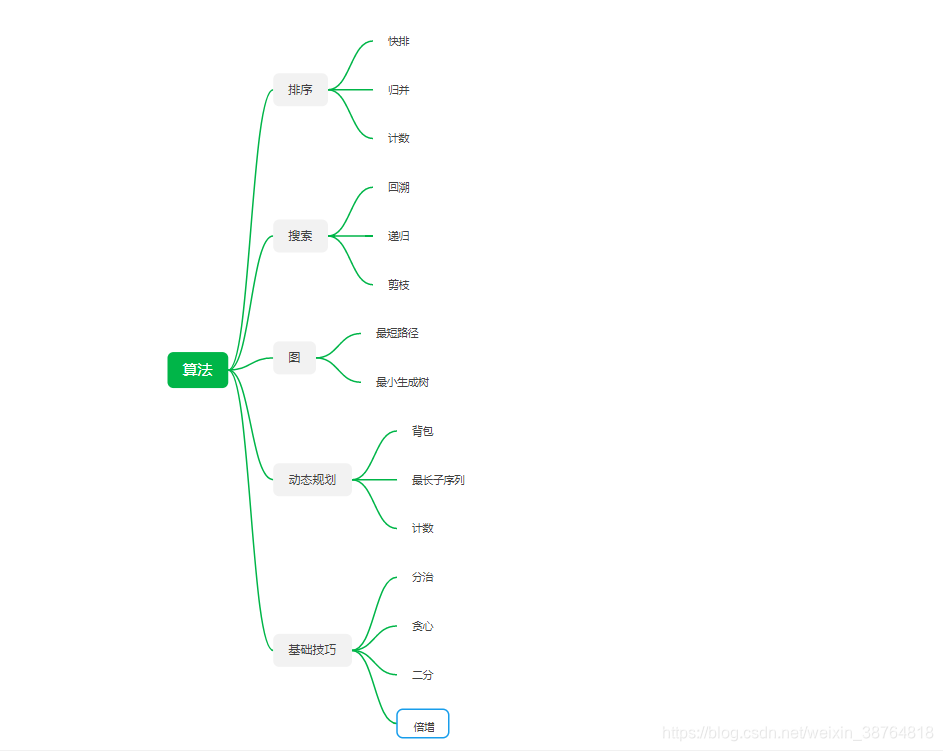
一.基本数据结构
1.数组、字符串
优点:
构建一个数组非常简单
能让我们在O(1)的时间里根据数组下标查询某个元素
缺点:
构建时必须分配一段连续的空间
查询、删除、添加某个元素时须遍历整个数组
2.链表
单链表:链表中的每个元素实际上是一个单独的对象,而所有对象都通过每个元素中的引用字段链接在一起。
双链表:双链表的每个结点中都含有两个引用字段。
优点:灵活分配空间
缺点:查询元素需要O(n)时间
解题技巧:
利用快慢指针(有时需要三个指针)
加链表头
例如:
两个排序链表进行整合排序
将链表的奇偶数按原定顺序分离,生成前半部分为奇数,后半部分为偶数的链表
3.栈
特点:后进先出
算法基本思想:
可以用一个单链表实现
只关心上一次操作
处理完上一次操作后,能在O(1)时间内查找到更前一次的操作。
4.队列
特点:先进先出
双链表实现
常用场景:
广度优先搜索
5.树
特点:结构直观
常考算法:递归
常考树的形状:
普通二叉树
平衡二叉树
完全二叉树
二叉搜索树
红黑树
树的遍历应用场景:
前序遍历:多应用于树的创建和搜索
中序遍历:二叉搜索树
后序遍历:在对某个节点进行分析的时候,需要来自左子树和右子树的信息。
二.高级数据结构
1.优先队列
与普通队列区别:
保证每次取出的元素是队列中优先级最高的
优先级别可自定义
常用场景:
从杂乱无章的数据中按照一定的顺序(或优先级)筛选数据
求前k个……的题目
本质:二叉堆
2.图
基本知识点:
- 阶、度
- 树、森林、环
- 有向图、无向图、完全有向图、完全无向图
- 连通图、连通分量
- 存储和表达方式:邻接矩阵、邻接链表
算法:
- 遍历:深度优先、广度优先
- 环的检测、树的检测:有向图、无向图
- 拓扑排序
- 最短路径算法
- 连通性相关算法:Kosaraju、Tarjan、求解孤岛数量、判断是否为树
- 图的着色、旅行商问题
- 联合-查找算法(Union-Find)
3.前缀树(字典树)
字典查找:例如给定一系列构成字典的字符串,要求在字典中找出所有以“ABC"开头的字符串
性质:
1.每个节点至少包含两个基本属性
- children:数组或集和,罗列出每个分支当中包含的所有字符
- isEnd:布尔值,表示该节点是否为某字符串的结尾
2.根节点是空的
3.除了根节点,其他所有节点都有可能是单词结尾,叶子节点一定都是单词的结尾。
基本操作:
1.创建:
- 遍历一遍输入的字符串,对每个字符串的字符进行遍历
- 从前缀树的根节点开始,将每个字符加入到节点的children字符集当中。
- 如果字符集已经包含了这个字符,则跳过
- 若当前字符是字符串的最后一个,则把当前节点的isEnd标记为真。
2.搜索:
从根节点出发,逐个匹配输入的前缀字符,如果遇到了就继续往下一层搜索,若没遇到就立即返回。
4.线段树
线段树:一种按照二叉树的形式存储数据的结构,每个节点保存的都是数组里某一段的总和。
5.树状数组
基本特征:
利用数组表示多叉树,和优先队列类似
优先队列是用数组来表示完全二叉树,而树状数组是多叉树
树状数组第一个元素是空节点
来源:CSDN
作者:親愛の小孩
链接:https://blog.csdn.net/weixin_38764818/article/details/104564490