假设对以下10个数进行快速排序:

我们先模拟快速排序的过程:首先,在这个序列中随便找一个数作为基准数,通常为了方便,以第一个数作为基准数。

在初始状态下,数字6在序列的第1位。我们的目标是将6挪到序列中间的某个位置,假设这个位置是k。现在就需要寻找这个k,并且以第k位为分界点,左边的数都小于等于6,右边的数都大于等于6。那么如何找到这个位置k呢?
我们要知道,快速排序其实是冒泡排序的一种改进,冒泡排序每次对相邻的两个数进行比较,这显然是一种比较浪费时间的。
而快速排序是分别从两端开始”探测”的,先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换他们。这里可以用两个变量iii和jjj,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵iii”和“哨兵jjj”。刚开始的时候让哨兵iii指向序列的最左边,指向数字6。让哨兵jjj指向序列的最右边,指向数字8。

首先哨兵jjj开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵jjj先出动,这一点非常重要。哨兵jjj一步一步地向左挪动(即j=j−1),直到找到一个小于6的数停下来。接下来哨兵iii再一步一步向右挪动(即i=i+1),直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前,哨兵iii停在了数字7面前。

现在交换哨兵$i$和哨兵$j$所指向的元素的值。交换之后的序列如下。
到此,第一次交换结束。接下来开始哨兵jjj继续向左挪动(再友情提醒,每次必须是哨兵j先出发)。他发现了4<6,停下来。哨兵iii也继续向右挪动的,他发现了9>6,停下来。此时再次进行交换,交换之后的序列如下。

第二次交换结束。哨兵jjj继续向左挪动,他发现了3<6,又停下来。哨兵iii继续向右移动,此时哨兵iii和哨兵jjj相遇了,哨兵iii和哨兵jjj都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下。

到此第一轮“探测”真正结束。现在基准数6已经归位,此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6。回顾一下刚才的过程,其实哨兵jjj的使命就是要找小于基准数的数,而哨兵i的使命就是要找大于基准数的数,直到i和j碰头为止。
关于边界值问题:
1.如果选取的基值是数组最左边的,则先让哨兵j先走,如果选取的基值是最右边的,则让哨兵i先走。
原因:一次快排结束后i一定是等于j的,哨兵i循环查看结束后i==j,哨兵j循环查找结束条件是找到一个比基值小的数,我们知道哨兵j先走,那么在上次排序后哨兵i指向的值一定是比基值小的,那么哨兵j查找结束后肯定会找到哨兵i,故结束时i =j。当哨兵i先走时,时哨兵i逼近哨兵j,那么最后结束后哨兵i指向的值是大于基值的,如果哨兵j先走,那么是哨兵j逼近哨兵i,那么结束时哨兵i指向的值是小于基值的,这样当选择最右边值做基值array[i] >temp,选择最左边值做基值时,array[i]<temp,这样交换array[i] 和temp就可以保证temp左边的值都小于等于temp,右边的值都大于等于temp(temp是基值)。
public static void sorts(int []nums,int begin,int end) {
if(begin<end) {
int i = quickSort(nums, begin, end);
sorts(nums, begin, i-1);//对基值左边的排序
sorts(nums, i+1, end);//对基值右边的排序, 去掉基值是因为他已经在正确的位置sh
//上以它不需要参与排序
}
}
public static int quickSort(int []nums,int begin,int end) {
int i = begin;
int j = end;
int temp = nums[begin];
while(i<j) {
while(j>i&&nums[j]>=temp) {
j--;
}
while(j>i&&nums[i]<=temp) {
i++;
}
if(i<j) {
int s = nums[i];
nums[i] = nums[j];
nums[j] = s;
}
}
nums[begin] = nums[i];
nums[i] = temp;
for (int k : nums) {
System.out.print(k+" ");
}
System.out.println();
return i;
}
时间复杂度分析:
快速排序最优的情况就是每一次取到的元素都刚好平分整个数组:

最坏时间复杂度就是每次划分只有基值某一侧有值,另一侧没有值
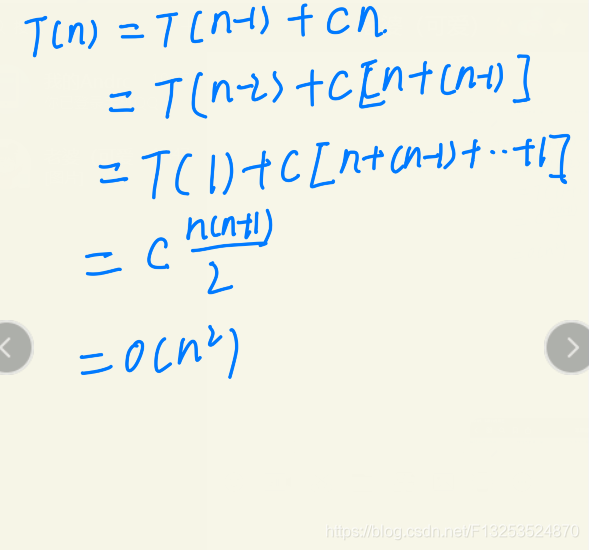
平均时间复杂度:
o(nlogn)
空间复杂度:
其实这个空间复杂度不太好计算,因为有的人使用的是非就地排序,那样就不好计算了(因为有的人用到了辅助数组,所以这就要计算到你的元素个数了);我就分析下就地快速排序的空间复杂度吧;
首先就地快速排序使用的空间是O(1)的,也就是个常数级;而真正消耗空间的就是递归调用了,因为每次递归就要保持一些数据;
最优的情况下空间复杂度为:O(logn) ;每一次都平分数组的情况
最差的情况下空间复杂度为:O( n ) ;退化为冒泡排序的情况
来源:CSDN
作者:F13253524870
链接:https://blog.csdn.net/F13253524870/article/details/104790933