在之前已经了解到神经网络是由一个一个的神经元来组成的,接下来学习神经网络的基础---神经元,从最简单的线性回归开始学起。
1. 直观上来看线性回归解决什么样的问题呢?
用最经典的房价预测来看,首先考虑最简单的情况,假定现在只看房价和面积的大小的关系,通过历史的经验我们可能能够有看到这样一些样本点:
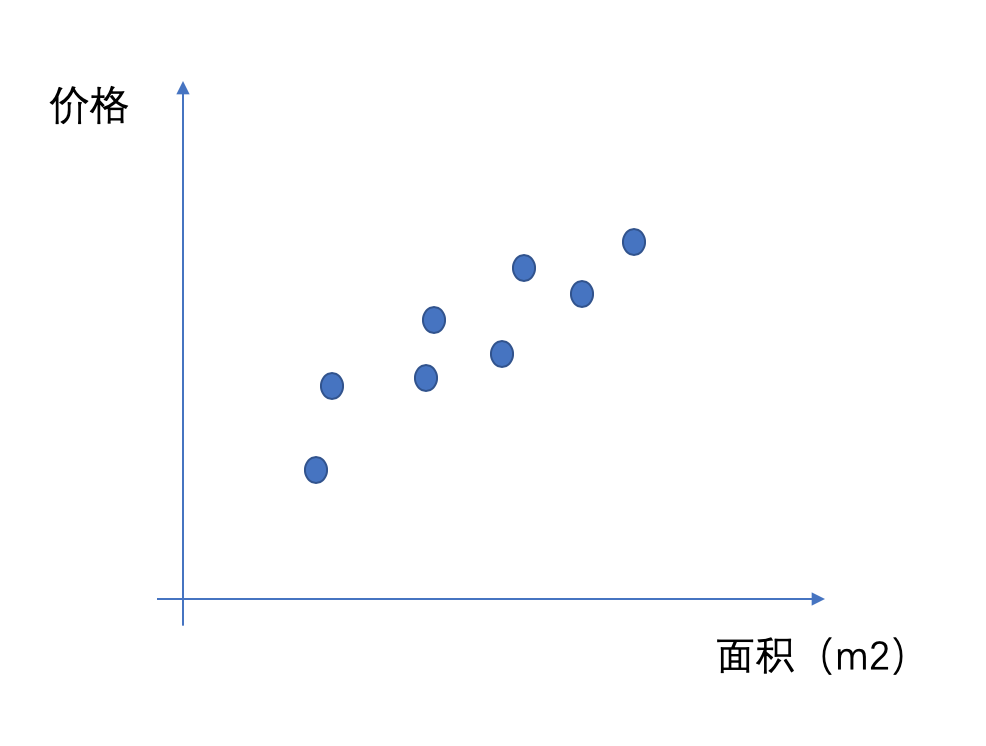
我们可以看到他们大概是呈一种正相关的关系,但是如果现在有一套新房,我们只知道他的面积,我怎么能够大概评估这个房子在什么价位呢?从最简单的角度来考虑,我们能不能找到一条直线来表达价格和面积之间的关系呢?
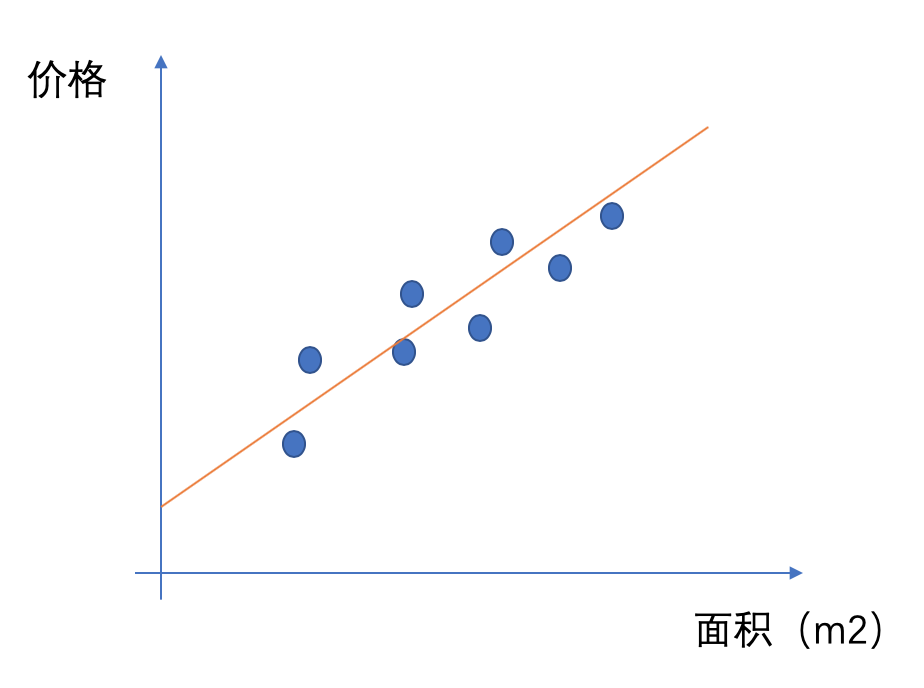
于是我们就有了一条直线来大概说明房价和面积之间是一种什么样的关系,这条直线用数学公式表达为:y_h = wx+b。但是在这个平面里面可以画无数条直线,哪一条直线是最好的呢?我们使用这条直线来预测房价,当然希望我在相同面积上面我预测的价格和实际的价格的差异越小越好,于是我们就有了优化的方向:Σ(h(x)-y)^2最小。
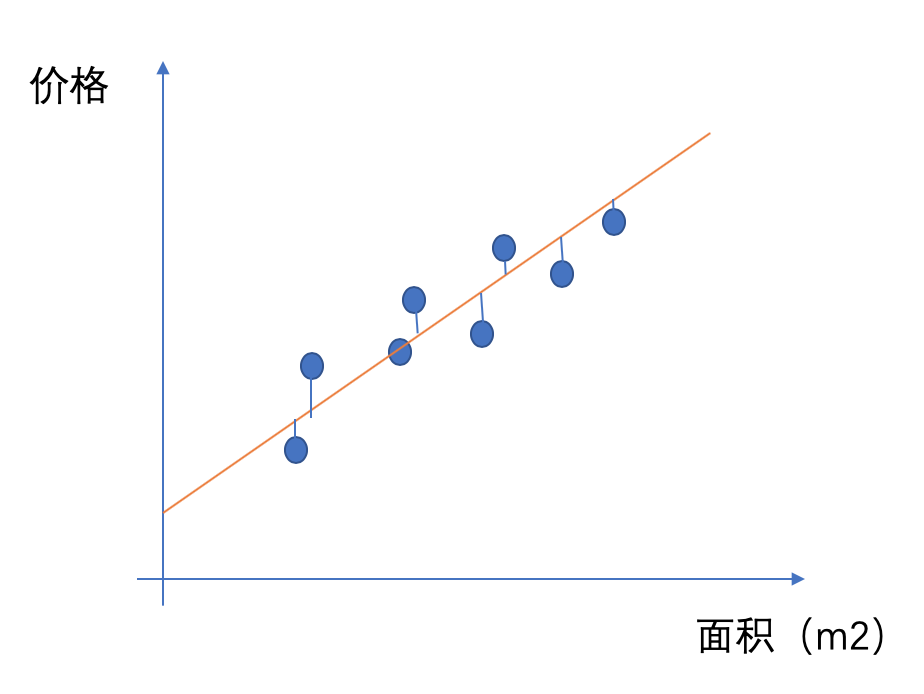
那怎么样去找到相关的参数,使得Σ(h(x)-y)^2,可以使用梯度下降法来实现。
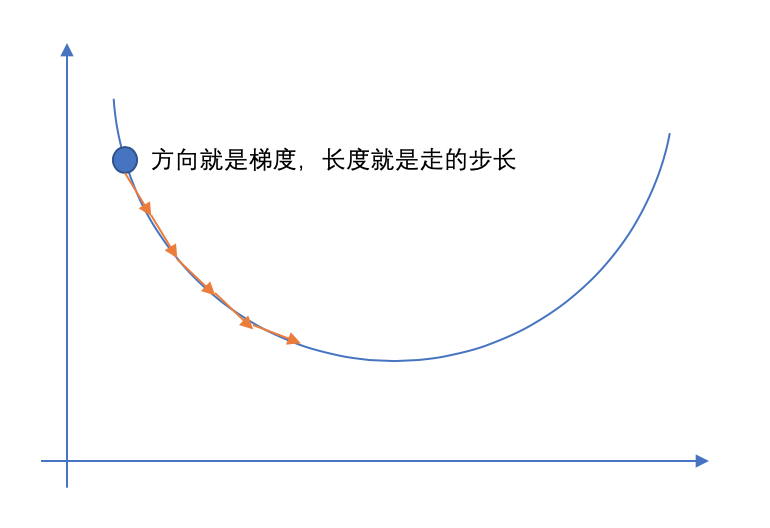
什么是梯度下降呢?
梯度下降就好比下山,上帝把你随机的放在了一座山的任意一个位置,但是现在你要下山去要怎么走呢?第一是确定一个方向,我们在不知道整座山的全貌的时候,就只好基于我们当前的形式来判断,环顾四周,我走向那个下降最快的方向,这个方向就是梯度,我们可以用偏导数来描述这个方向。第二步是确定按照这个方向走多远,这个在一定程度上决定了我们下山的效率,如果每走一小步都要停下来去看看四周,然后再走下一小步,那这样效率就太低了。如果要是定的距离太长了,那有可能就走过了最低点,所以步长的选择是比较重要的。比如:有一种方法是随着你走得越缓,就将你的步长放小一点,避免走过头了。
那我们在对这样一个问题的线性回归就可以描述为,找到一个参数w和b,使得Σ(h(x)-y)^2,那我们就用这条直线来表示面积和房价间的关系。当然,房价不仅仅只和面积有关,还和地段、配套设施等有关系,那我们推而广之,假设这些特征和房价之间都存在线性关系,我们用这样一个函数来拟合各个特征和房价的关系:h(x)=w1*x1+w2*x2+...+wn*xn+b,通过这样来对房价进行预测。
从神经元的角度来看线性回归是这样的:

2. 从数学模型角度来看线性回归:
模型:h(x)=w1*x1+w2*x2+...+wn*xn+b
损失函数:J(w,b) =1/2mΣ(h(xi)-yi)2
要使得损失函数:J(w,b) 最小,我们利用梯度下降算法来实现。
J(w)的梯度为:
∂J/∂w=1/mΣ(h(xi)-yi)xi
∂J/∂b=1/mΣ(h(xi)-yi)
梯度下降:
w:=w-aplha*∂J/∂w
b:=b-alpha*∂J/∂b
这样就实现了批梯度下降算法(BGD)。
批梯度下降法每次学习都使用整个训练集,因此每次更新都会朝着正确的方向进行,最后能够保证收敛于极值点,凸函数收敛于全局极值点,非凸函数可能会收敛于局部极值点,缺点就是学习时间太长,消耗大量内存,特别是在数据量很大的情况下。
这里有两种解决方法,一种是随机梯度下降法(SGD),随机取一个样本来进行梯度的计算和更新,由于每次只使用一条数据来计算,计算速度非常快。SGD的缺点在于每次更新可能并不会按照正确的方向进行,从而导致损失函数剧烈波动,而且无法判断是否收敛。但是有可能会歪打正着,如果目标函数有盆地区域,SGD会使优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点,这样对于非凸函数,可能最终收敛于一个较好的局部极值点,甚至全局极值点。
另一种是小批量梯度下降法(MBGD),其实就是在BGD和SGD之间取了折中,每次取一个小批量的数据来进行梯度的计算和更新,如果Batch Size选择合理,不仅收敛速度比SGD更快、更稳定,而且在最优解附近的跳动也不会很大,甚至得到比BGD更好的解。
在这之外针对震荡问题还有Momentum梯度下降法/NAG梯度下降法,还没有理解透,回头再补充进来。
3. 实现代码:
在代码实现中,实现了两种,一种是批梯度下降法(BGD),一种是小批量梯度下降法(MBGD),代码写得不好,画图部分大家可以自己加上,各位大佬拍砖。
1 import numpy as np
2 import random
3 import time
4
5
6 #构建数据集:
7 num_features = 2
8 num_samples = 10000
9 true_w = [1,3.5]
10 true_b = 3
11 #构建一个m个样本,2个特征的数据集
12 features = np.random.normal(scale=1,size=(num_samples,num_features))
13 print(features.shape)
14 #print(time.time())
15 labels = np.dot(features,true_w)+true_b
16 print(labels.shape)
17 labels += np.random.normal(scale=0.01,size=(num_samples,))
18 #后面这种形式的运行速度会更快一点
19 #labels2 = true_w[0]*features[:,0]+true_w[1]*features[:,1]+true_b
20
21 #定义线性回归模型
22 def linear_reg(w,b,X):
23 y_h = np.dot(X,w.T)+b
24 return y_h
25
26 #定义损失函数,1/2*(y_h-y)^2来衡量的平方损失函数
27 def square_loss(y_h,y,m):
28 #如果不做reshape,y.shape(1000,)在numpy中当作,在加减的时候会变成(1000,1000)
29 diff = y_h-y.reshape(m,1)
30 return (1./2/m)*np.dot(diff.T,diff)
31
32 #计算损失函数的梯度
33 def gradient_cal(X,y_h,y):
34 m,var = X.shape
35 gradw = np.zeros(var)
36 gradb = 0
37 #计算每个样本的偏导数,然后相加
38 for i in range(m):
39 for j in range(var):
40 gradw[j] += X[i][j]*(y_h[i]-y[i])
41 gradb += y_h[i]-y[i]
42 gradw=gradw/m
43 gradb=gradb/m
44 return gradw,gradb
45
46 #批梯度下降:每次都对所有的样本计算梯度,然后再更新参数
47 #alpha:学习速度
48 #eporchs:迭代轮数
49 #threshold:损失函数阈值
50 #X,y
51 def BGD(alpha,eporchs,threshold,X,y):
52 iter_count=0
53 w=np.random.normal(scale=1,size=(1,X.shape[1]))
54 b=0
55 m=X.shape[0]
56 y_h = linear_reg(w,b,X)
57 loss = square_loss(y_h,y,m)
58 while iter_count<eporchs and loss>threshold:
59 y_h = linear_reg(w,b,X)
60 gradw,gradb = gradient_cal(X,y_h,y)
61 w = w-alpha*gradw
62 b = b-alpha*gradb
63 # y_h = linear_reg(w,b,X)
64 loss = square_loss(y_h,y,m)
65 iter_count+=1
66 print("iter_count: ", iter_count, "the loss:", loss)
67 return w,b
68
69
70 #定义每次随机取一批数据
71 #总体思路:先生成一个乱序的长度等于样本数量的index list,然后每次取batch_size个,如果取到最后一个批次的时候就取到最后一个
72 #参数:batch_size,每批数据的大小
73 def data_iter(X,y,batch_size):
74 m = X.shape[0]
75 indecies = list(range(m))
76 random.shuffle(indecies)
77 for i in range(0,m,batch_size):
78 j = np.array(indecies[i:min(i+batch_size,m)])
79 yield X[j],y[j]
80 #小批量梯度下降,每次只用部分数据来更新参数
81 #alpha:学习速度
82 #eporchs:迭代轮数
83 #threshold:损失函数阈值
84 def MBGD(alpha,eporchs,threshold,features,labels):
85 #初始化
86 iter_count=0
87 w=np.random.normal(scale=1,size=(1,features.shape[1]))
88 b=0
89 loss = square_loss(linear_reg(w,b,features),labels,num_samples)
90 print(loss)
91 #对每个批量数据进行参数的更新
92 while iter_count<eporchs and loss>threshold:
93 for X,y in data_iter(features,labels,50):
94 y_h = linear_reg(w,b,X)
95 m=X.shape[0]
96 gradw,gradb = gradient_cal(X,y_h,y)
97 w = w-alpha*gradw
98 b = b-alpha*gradb
99 # y_h = linear_reg(w,b,X)
100 loss = square_loss(linear_reg(w,b,features),labels,num_samples)
101 iter_count+=1
102 print("iter_count: ", iter_count, "the loss:", loss)
103 return w,b
104
105 #执行对比,可以调整不同的参数来看看效果,MBGD收敛速度比BGD速度快很多
106 if __name__ == '__main__':
107 start = time.time()
108 w,b=MBGD(0.03,10,1e-4,features,labels)
109 middle = time.time()
110 print(middle-start,w,b)
111 w,b=BGD(0.03,10,1e-4,features,labels)
112 end = time.time()
113 print(end-middle,w,b)
来源:https://www.cnblogs.com/4man1woman/p/10118534.html