范数

什么是范数？

       范数（Norm）是一个表示向量“长度”的函数，为向量空间内的所有向量赋予非零的正长度或大小。
       下面简单地介绍以下几种向量范数的定义和含义。

1、$l_p$范数
       对于一个 $n$维向量 $\vec v$ ，一个常见的范数函数为 $l_p$ 范数。它代表了一组范数。其定义如下：
$l_p(\vec v)\equiv \Vert \vec v\Vert_p=\left( \sum_{i=1}^{n}\vert v_i\vert ^p\right)^{1/p}$
       其中，常用的 $p$ 的取值有 1，2，$\infty$等。

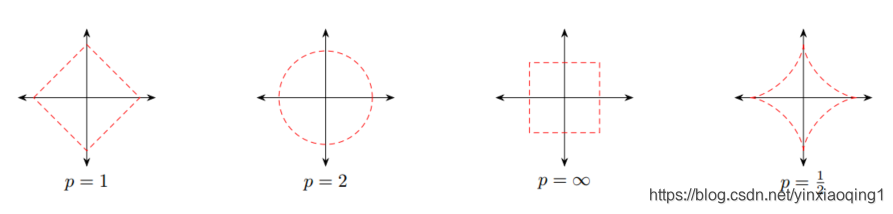
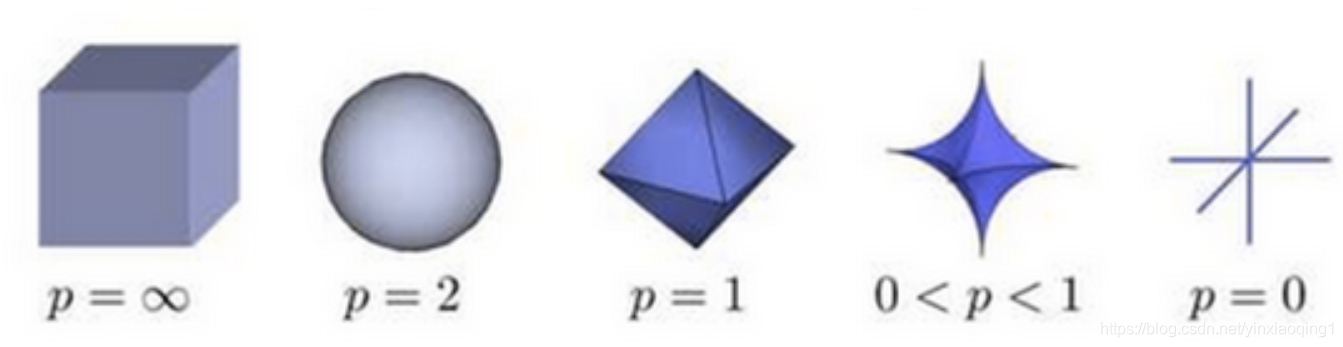       上图为 p 从0到无穷变化时，二维和三维空间到原点的距离（范数）为1的点构成的图形的变化情况。

2、$l_1$范数
       $l_1$ 范数为向量的各个元素的绝对值之和。
$\Vert \vec v \Vert_1=\sum_{i=1}^n\vert v_i\vert$

       $l_1$范数有很多的名字，例如我们熟悉的曼哈顿距离、最小绝对误差等。使用$l_1$范数可以度量两个向量间的差异，如绝对误差和（Sum of Absolute Difference）等。
       由于 $l_1$ 范数的天然性质，对 $l_1$ 优化的解是一个稀疏解，因此 $l_1$ 范数也被叫做稀疏规则算子。通过L1可以实现特征的稀疏，去掉一些没有信息的特征，例如在对用户的电影爱好做分类的时候，用户有100个特征，可能只有十几个特征是对分类有用的，大部分特征如身高体重等可能都是无用的，利用 $l_1$ 范数就可以过滤掉。

3、$l_2$范数
       $l_2$ 范数为向量的各个元素的平方和再开方。
$\Vert \vec v \Vert_2=\sqrt{\sum_iv_i^2}$

       它也有很多的名字，例如欧氏距离。像 $l_1$ 范数一样， $l_2$ 也可以度量两个向量间的差异，如平方差和（Sum of Squared Difference）。
       L2范数通常会被用来做优化目标函数的正则化项，防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力。

4、$l_\infty$范数
       $l_\infty$ 范数为向量的各个元素的最大绝对值。

参考文献：
几种范数的简单介绍
神经网络与深度学习-邱锡鹏

来源：CSDN

作者：yinxiaoqing1

链接：https://blog.csdn.net/yinxiaoqing1/article/details/104632849