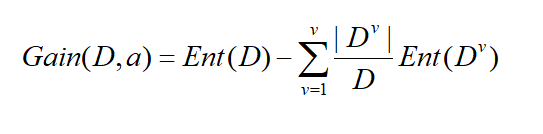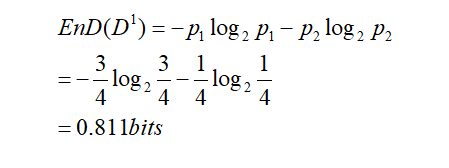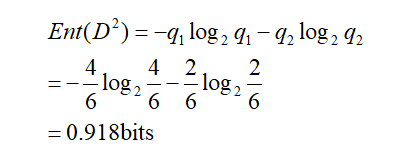决策树原理（一）

        小伙伴们，欢迎浏览我的博客，从今天开始，我将为大家开始讲解机器学习的基础算法，如决策树、KNN算法、SVM、神经网络等。本节先讲解决策树算法。

        一、机器学习中分类与预测算法评估

           1、准确率

            2、速度

            3、强壮性

            4、可规模性

            5、可解释性

        在机器学习算法当中、评价一个算法的好坏或者比较两个算法的优劣，主要以上5个方面进行评估。首先准确率是指算法分类或者预测的准确程度，这是个非常重要的标准，而速度是指算法的复杂度高不高，其次强壮行是指一个算法在包含噪音、缺失值、异常值的数据中依然保持非常好的效率 ，可规模性是指一个算法不仅可以在小规模数据上保持高效，在呈指数型增长的数据中依然能保持高效，最后可解释性是指算法在做出特征值的选取和归类能容易的解释这种归类和我们的直觉是相符的。

        二、决策树

        1、什么是决策树/判定书（decision tree）？

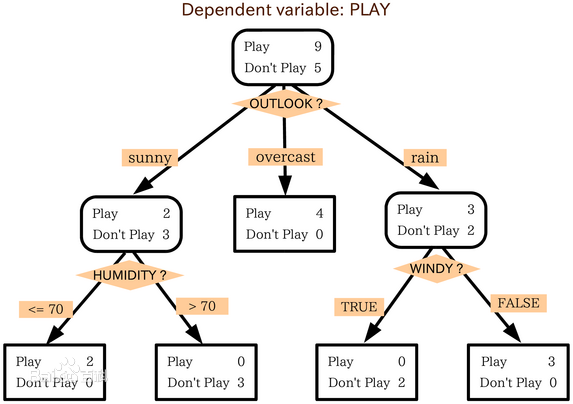
             决策树是类似于流程图的树结构：其中，每个内部节点表示在一个属性上的测试，每个分支表示一个属性的输出，而每个树叶节点表示一个类或者类分布。树的最顶层是根节点。

                                                                        

             以上图为例，该决策树的属性有：OUTLOOK、HUMIDITY、WINDY，以OUTLOOK属性为根节点，OUTLOOK有三个取值，即sunny、overcast、rain，根节点的三个分支就是它三个值的输出。决策树有五个叶子，叶子代表已经分好的类，即Play或者Don't Play。

             2、构造ID3决策树基本算法

            概念            

            信息熵（entropy）：     

                信息和抽象，如何度量？

                1948年，香农提出了 ”信息熵(entropy)“的概念

                一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者          

                是我们一无所知的事情，需要了解大量信息==>信息量的度量就等于不确定性的多少

                所以信息熵就是指信息的不确定度，不确定度越高，信息越复杂。

               样本D中第i个类样本所占的概率为p_i(i=1,2,3,.....y)，则信息熵的定义公式为：

  

             信息增益（information gain）

               我们继续了解信息增益

               假定离散属性a有V个可能的取值｛a¹,a²,a³.....a^v｝,比如性别有｛男，女｝两个取值，若用a属性对样本集进行划分，可以得到V个分支节点，其中第V个节点，包含了D所有再a属性上取值为a ^v的样本，记为D^v，我们根据上面的信息熵的公式可以算出D^v的信息熵，显而易见，每个分支所包含的样本数是不一样的，所以给每个分支赋予权重|D^v|/|D|，就是说，分支的样本数量多的对分支影响越大。则可以算出属性a对样本集D划分所得到的“信息增益”，以下为信息增益的公式：

一般来说，信息增益越大，属性a对样本集D划分纯度越到，因此信息增益大的优先作为决策树的属性节点。所以以信息增益为准则来选择划分属性。

 

            来，我们直接上例子

 

               

          这是一个电脑销售的记录，表示为样本D，显而易见，表中有四个测试属性，即age、income、student、credit_rating，一个分类属性，即buys_computer 。age属性取值有｛youth ，middle_aged，senior｝、income属性取值有｛low、medium、high｝、student｛yes、no｝、credit_rating属性取值为｛fair、excellent｝。现在·以各属性的信息增益为准则，选出决策树的根节点。

          现在以income属性为例，income属性取值有｛low、medium、high｝，则将对样本D划分为三个分支，得到三个子集，分别记为D¹=｛income=low｝ ，D² =｛income=medium｝，D³ =｛income=high｝ 。D1包含的编号有｛5，6，7，9｝的4个样例，buys_computer为yes的有3例，即p1=3/4，为no有1例，即p2=1/4，D2包含的编号有｛4，8，10，11，12，14｝的6个样例，正例占q1=4/6，反例占q₂=2/6，D³包含的编号有｛1，2，3，13｝的4个样例，正例占o₁=2/4，反例占o₂=2/4。

         根据信息熵的公式，先计算根节点的信息熵，样本集D有14个样例，正例占p=9/14，反例占q=5/14：

这里忘记说明，信息熵的单位是比特（bits）

         现在算出根据income属性划分三个分支的信息熵：

   D²的信息熵为：

 

 D³的信息熵为：

 

于是 根据信息增益公式，得出incomg属性的信息增益：

类似于同样的原理，算出age、student、 credit_rating三个属性的信息增益，得Gain(age) =0.246 , Gain(student) = 0.151, Gain(credit_rating)=0.048

 所以，选择age作为第一个根节点。

 通过第一次划分，得到下图的结果

按照 同样的原理，再算出各个属性节点的信息增益，对属性节点再次划分，划分终点的依据是节点包含的样本集都属于一类。

以上就是ID3决策树原理和实例演算的全过程。请读者耐心去将例子演算完毕，得出最终的决策树。

 

3 其他算法：
           在决策树算法中，ID3决策树只是一种常用的算法，还有更多的算法

           1、C4.5:  Quinlan

             2、Classification and Regression Trees (CART): (L. Breiman, J. Friedman, R. Olshen, C. Stone)

 着两个算法和ID3有共同点也有区别              

            共同点：都是贪心算法，自上而下(Top-down approach)

            区别：属性选择度量方法不同： C4.5 （gain ratio), CART(gini index), ID3 (Information Gain)

关于这两个算法，我再后续发表的文章会继续讲解，请继续关注我的博客。

 

4、决策树的优缺点

 决策树的优点：

     直观，便于理解，小规模数据集有效     

 

决策树的缺点：

     处理连续变量不好

     类别较多时，错误增加的比较快

     可规模性一般

 

 下一篇文章是  决策树应用（一），敬请期待

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

来源：https://www.cnblogs.com/xlandll/p/9212774.html