图论整理 | 易学教程

图的基本概念

根据之前博客数据结构整理中，我们可以知道

是一种线性数据结构

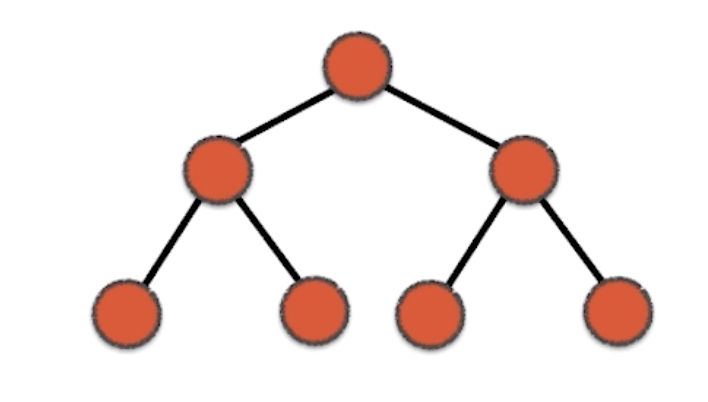
是一种树结构

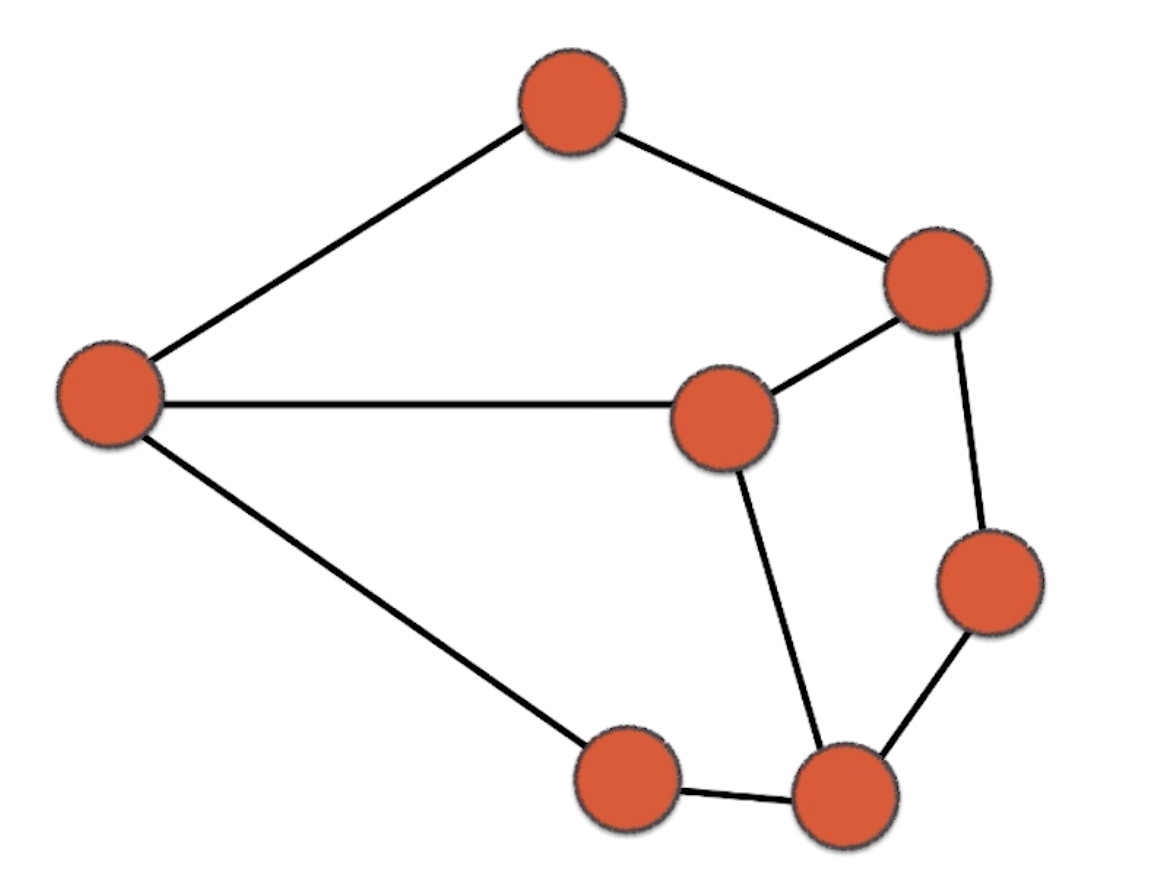
而这样一种结构就是一种图的结构

图的每一个点称为顶点(Vertex),通常我们会给顶点标上序号，而这些序号就可以理解为索引

当然这是一种抽象后的概念，在实际中，图可以表示为很多，比如社交网络

顶点与顶点相连的称为边(Edge)

而由以上的图中，由于各个顶点相邻的边是没有方向的，所以这种图又被称为无向图(Undirected Graph)，在无向图中，只要两个顶点相连，那么无论从哪个顶点出发都可以到达相邻的顶点。而类似于下图的图是有方向的

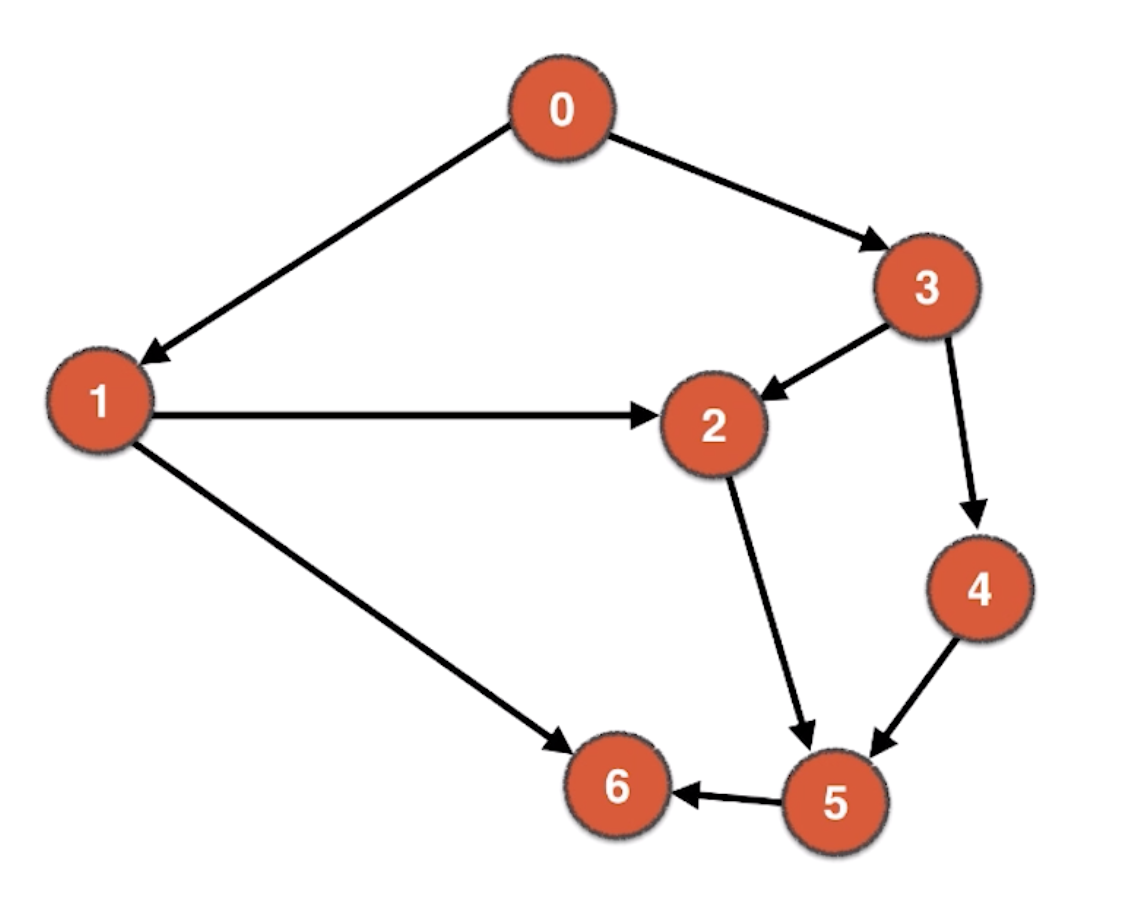
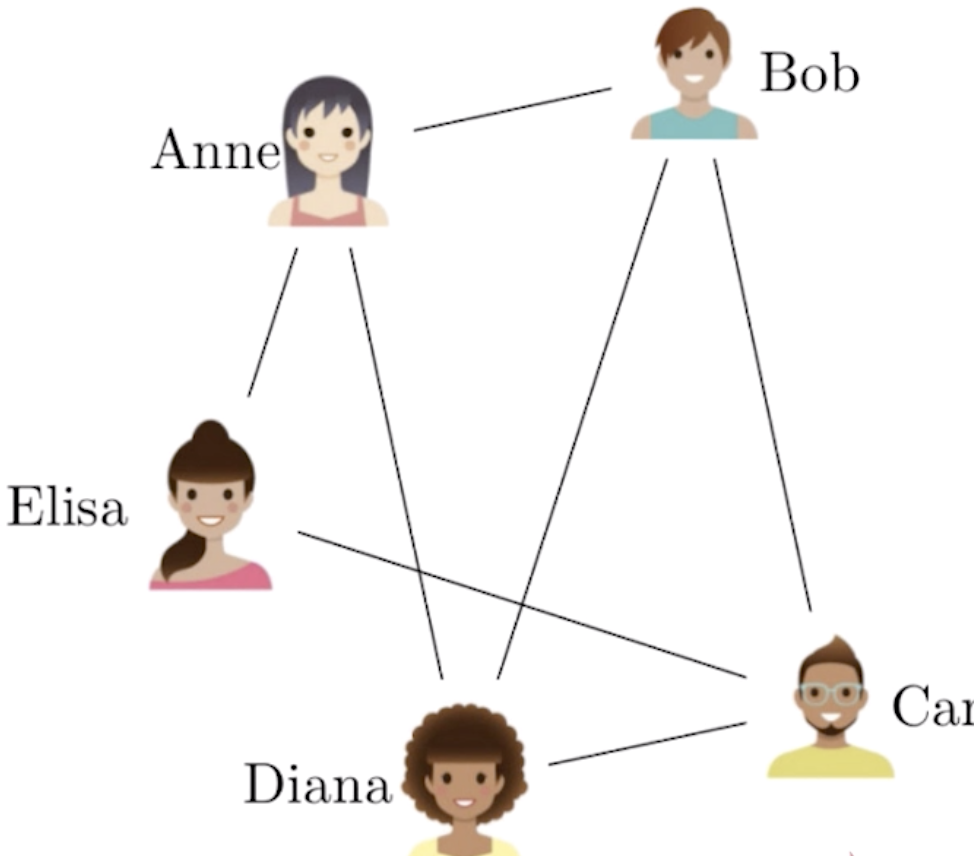
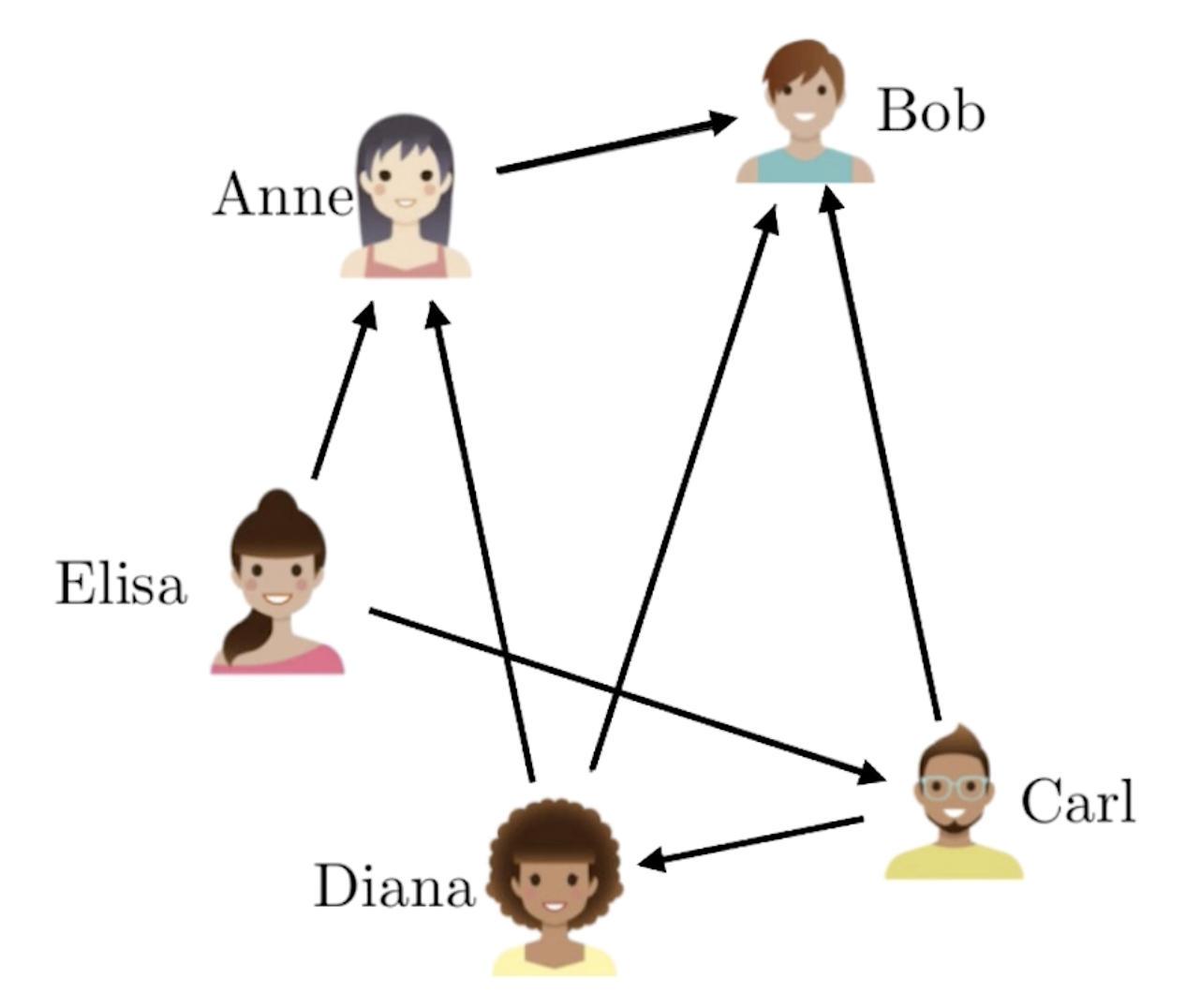
我们称之为有向图(Directed Graph)，在有向图中，只能够从起始顶点出发到达方向末端的相邻顶点，相反则不可以。所以我们在考虑现实关系建模的时候，要使用无向图还是有向图，比如地铁站点之间，无论从哪个站点出发都可以到达相邻的同一个线路的站点，所以要使用无向图。在社交网络中，如果是微信中，可以使用无向图，因为微信中人与人的关系是好友的关系。但有一些社交工具可能是一种关注的关系，而不是好友的关系。比如像下图中，Anne关注了Bob,而Bob并没有关注Anne,这样我们就必须使用有向图来进行建模。

如果一个图中，顶点与顶点的边只代表一种关系，而没有任何实际的度量，我们可以称这种图为无权图。而在有一些图中，它们的边代表具有一定的度量信息的意义。我们称这样的图为有权图。而这个权指的就是这些度量信息。

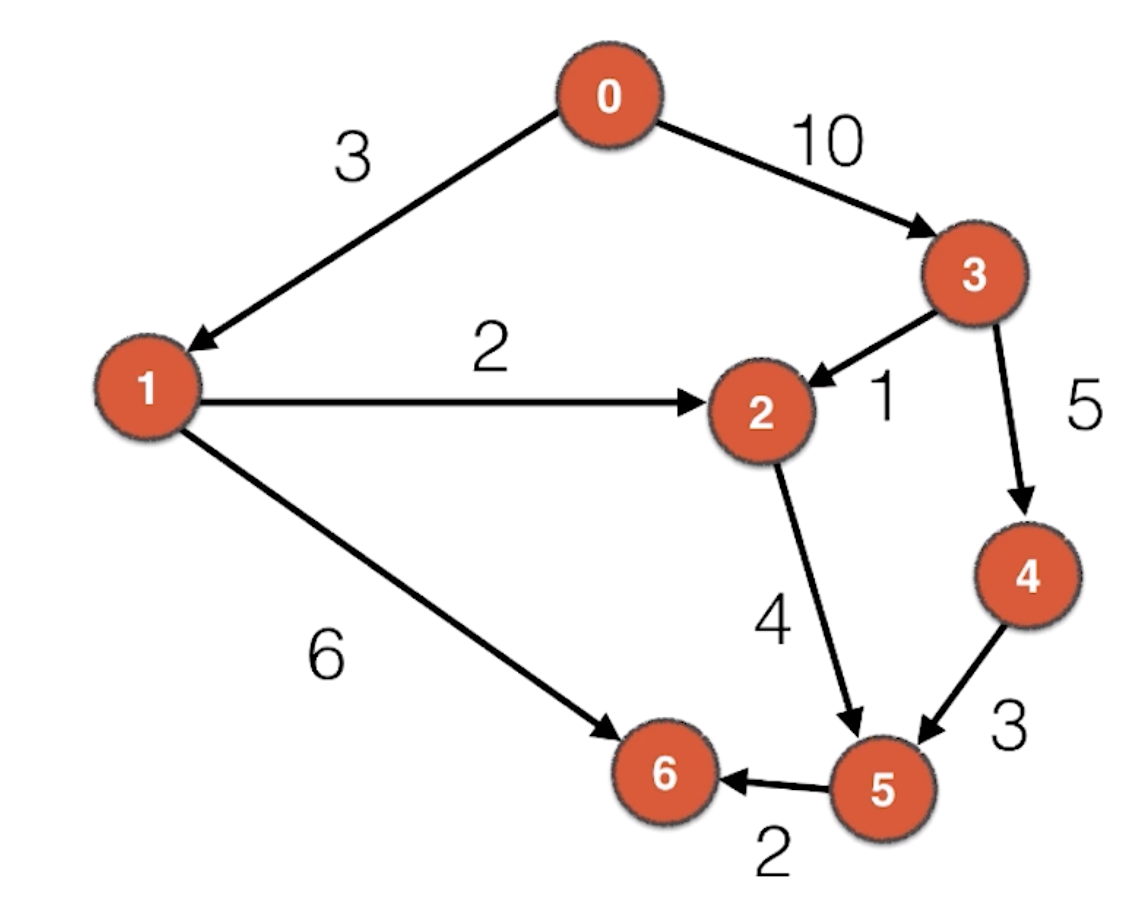
所以图的分类可以分为四种:

无向无权图
有向无权图
无向有权图
有向有权图

对于图的算法有一些只适合于某一类图，比如最小生成树算法只适用于有权图，拓扑排序算法只适用于有向图，最短路径算法虽然适用于所有类型的图，但是对于无向图和有向图的方式是不一样的。

在无向无权图中的概念

如果两个顶点之间有边，我们称为两点相邻

和一个顶点相邻的所有的边，我们成为点的邻边

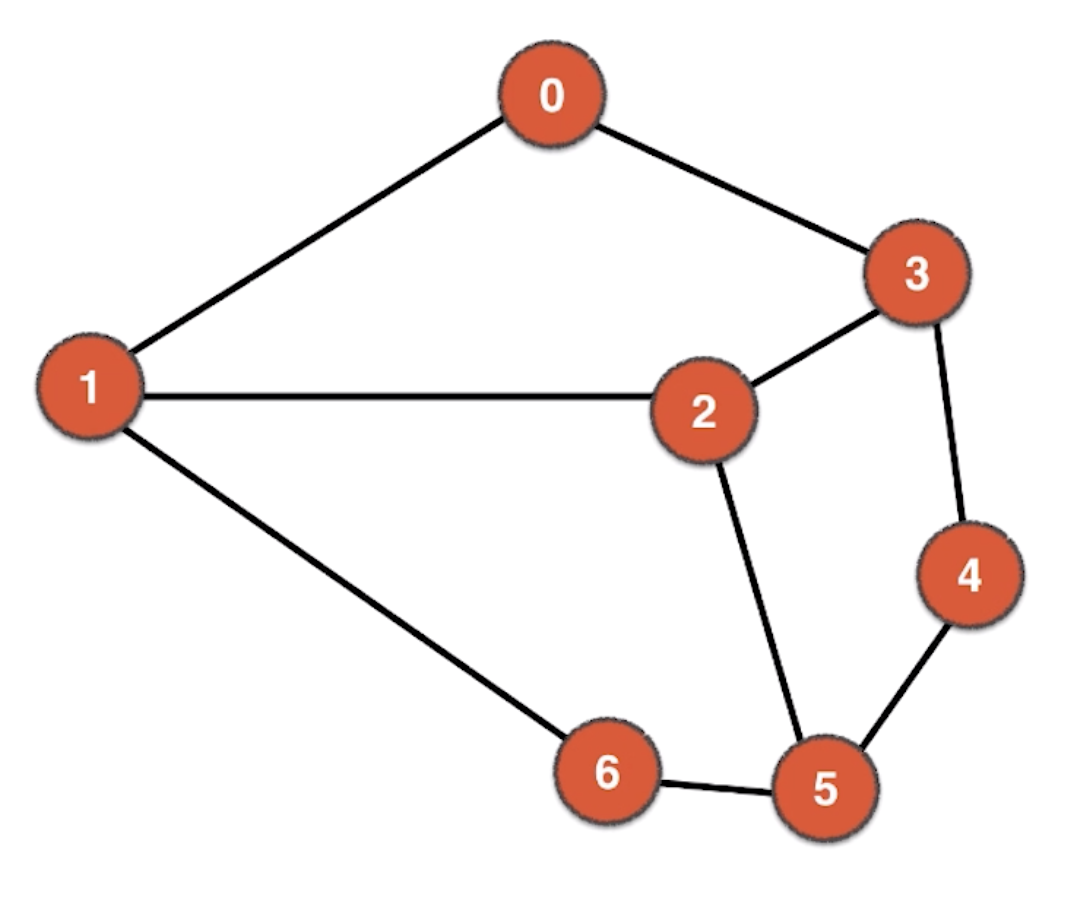
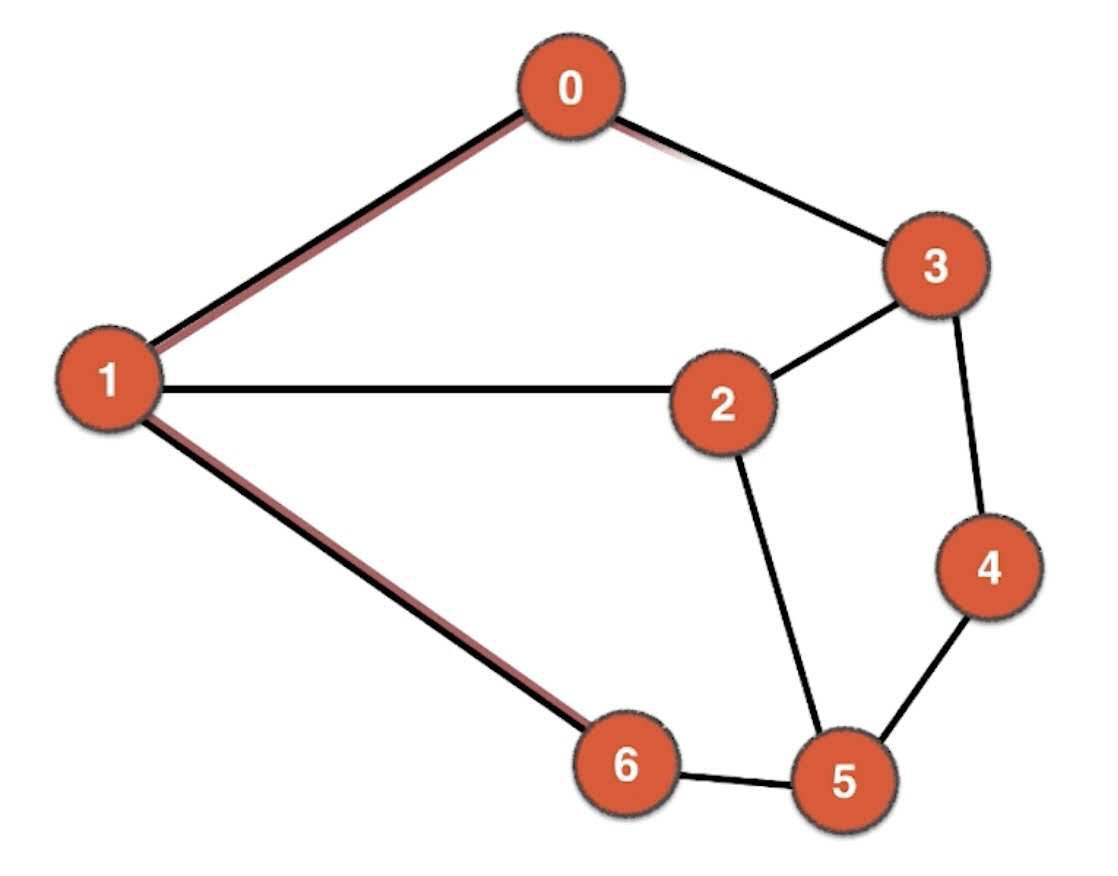
从一个顶点到另一个顶点所经过的所有边，我们称为路径(Path)，比如下图中从0到6经过了0-1-6，当然从0到6不一定只有这一条路径。

从一个顶点出发，经过其他顶点最终回到起始顶点，我们称之为环(Loop),比如下图中的0-1-2-3-0就是一个环，当然0-1-6-5-4-3-0也是一个环。

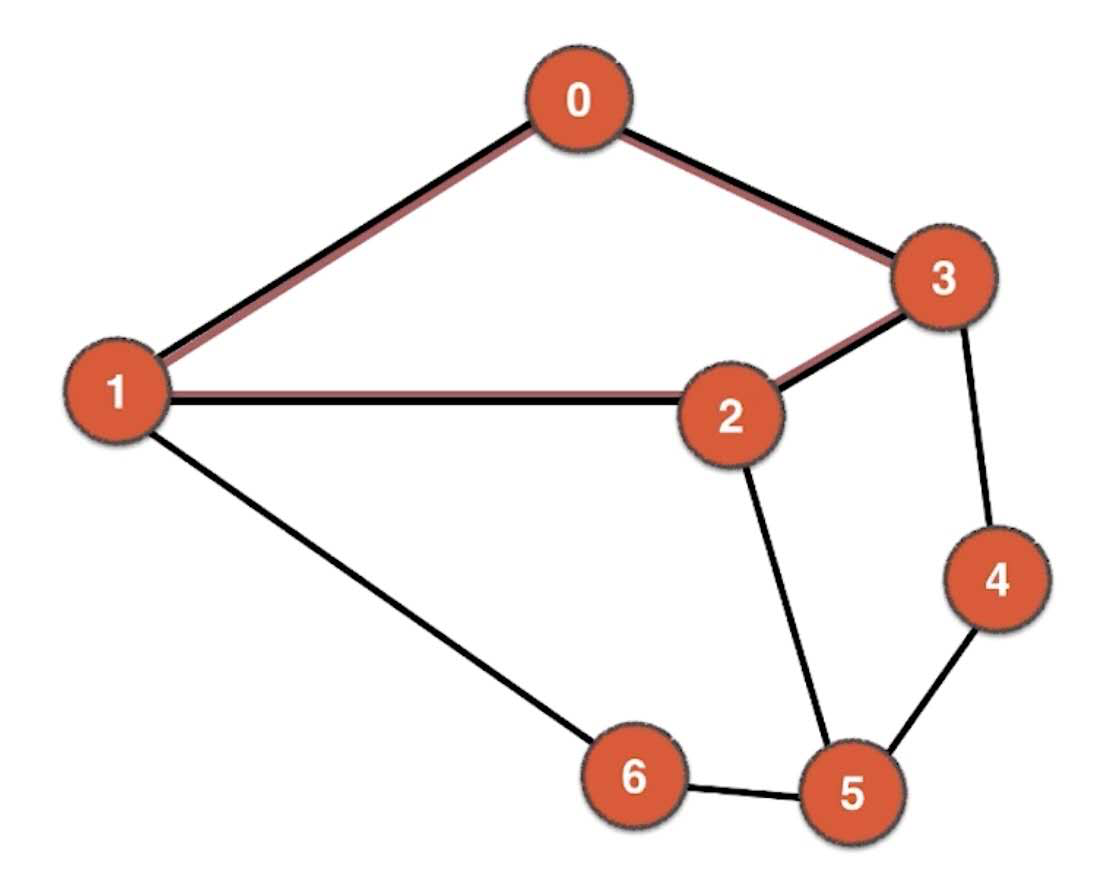
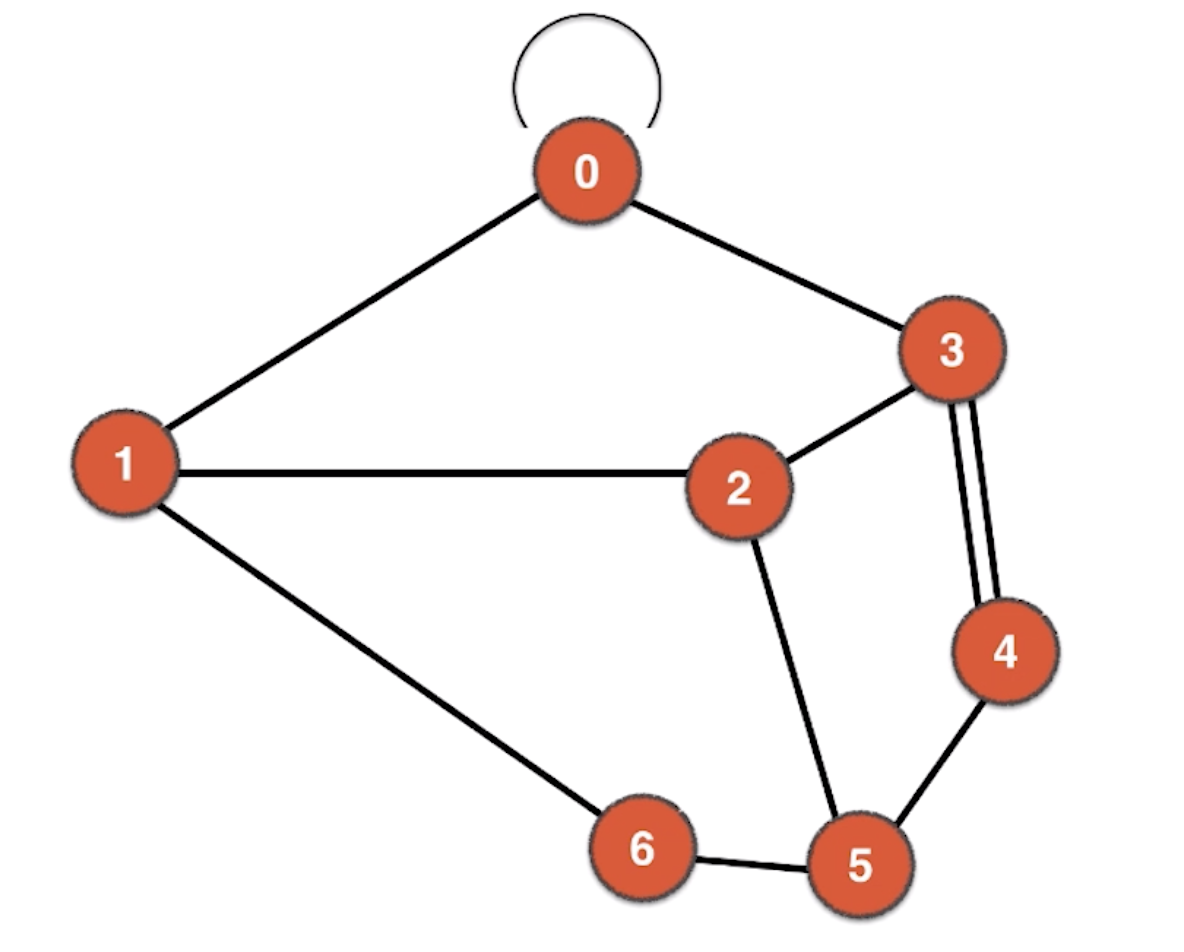
对于单个顶点来说也可以有一条自己到自己的边，我们称为自环边,如下图中的0-0。每两个相邻到顶点也可能不只一条边，我们可以称为平行边，如下图中的3-4。大多数情况下自环边和平行边没有意义，一般我们在处理自环边和平行边的时候都是先将其去除，变成没有自环边和平行边的图。当然也有自环边和平行边存在意义的场景，但是这种情况比较少。在图论中，我们称没有自环边和平行边的图为简单图。

当然在一个图中，并不是所有的顶点都必须是相连的

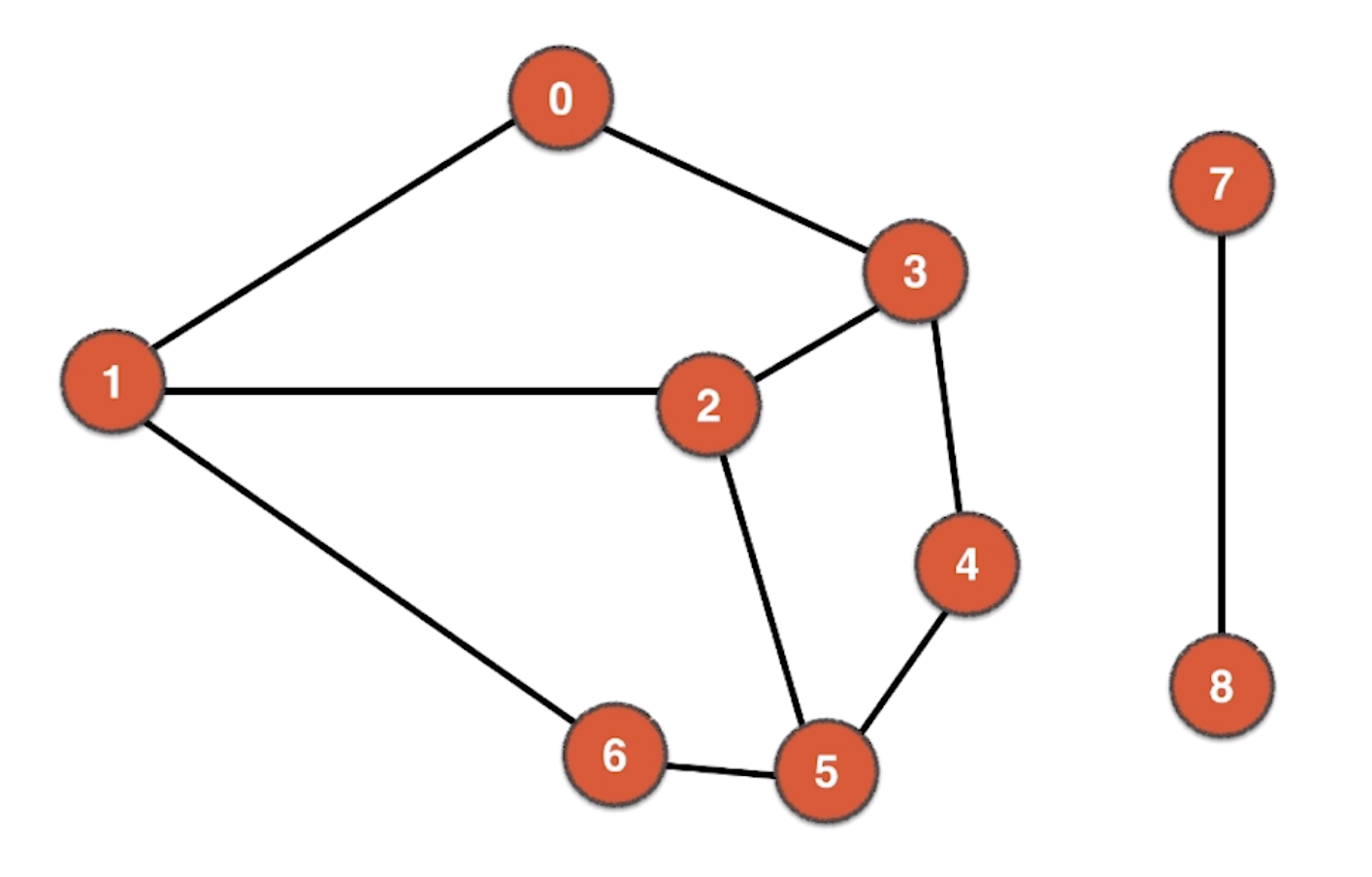
我们称在一张图中可以相互连接抵达的顶点的集合为联通分量，所以上面这张图中就有2个联通分量。因此一个图的所有节点不一定全部相连。一个图可能是有多个联通分量。

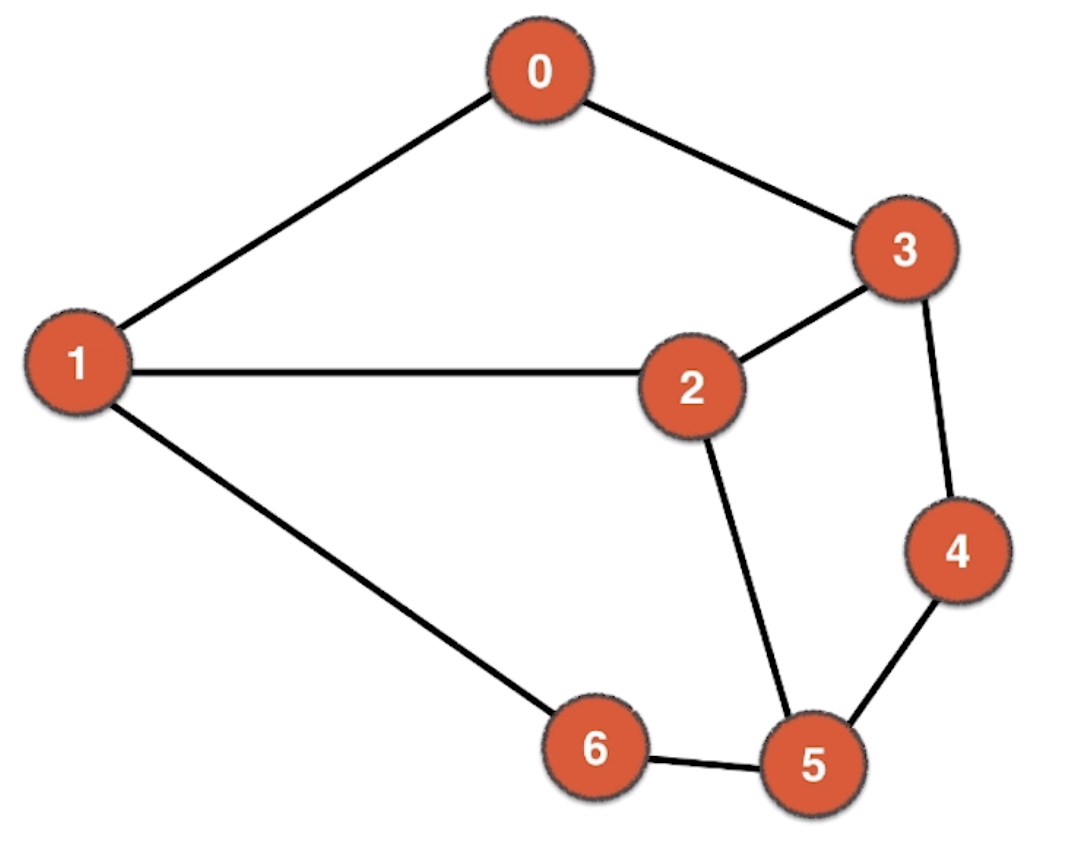
这种有环的图，我们可以称为有环图。

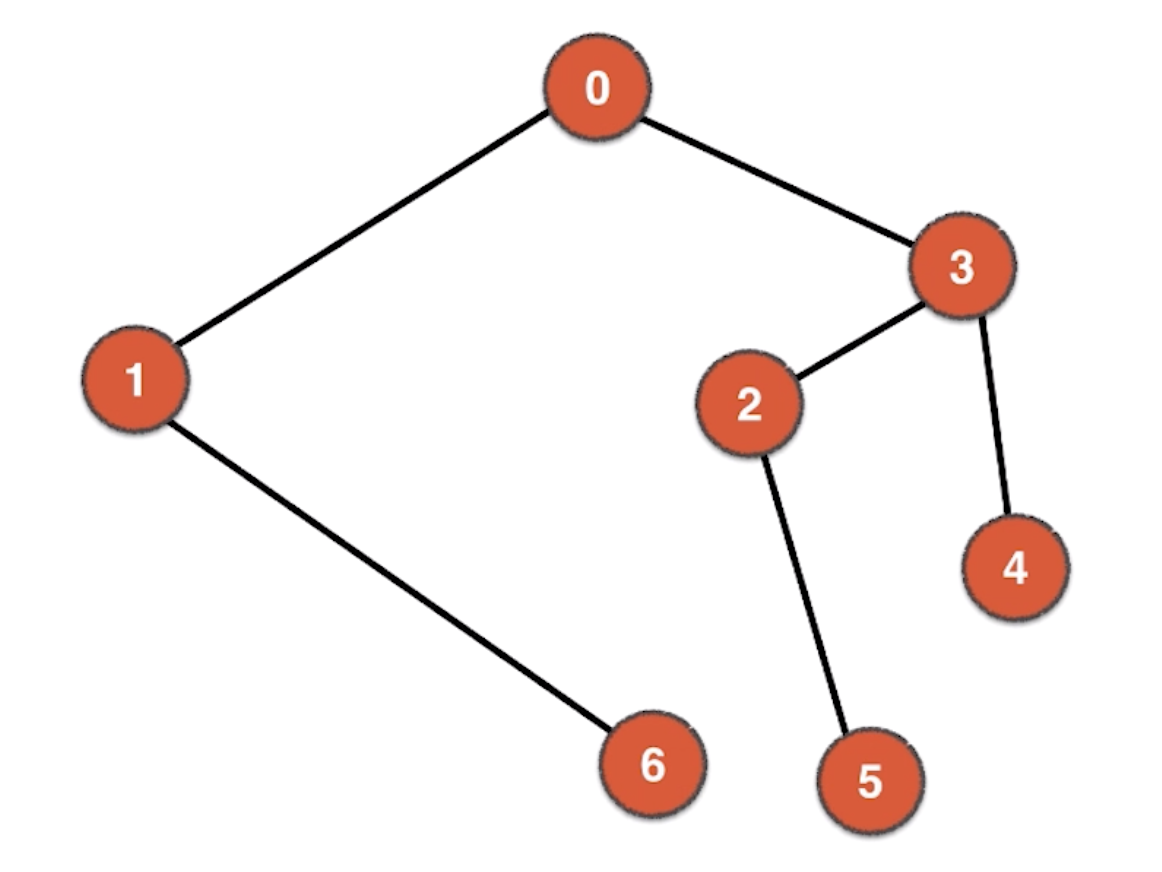
像这种无法找到从一个顶点出发，经过其他顶点又回到起始顶点的，我们称为无环图。但它又满足树的定义的，所以树是一种无环图。我们在图论中谈到树的定义跟在数据结构中说的树不完全是一个概念，图论中的树的根节点可以是任意节点，而数据结构中说的树往往是固定的一个根节点。虽然树是一种无环图，但一个无环图不一定是树。

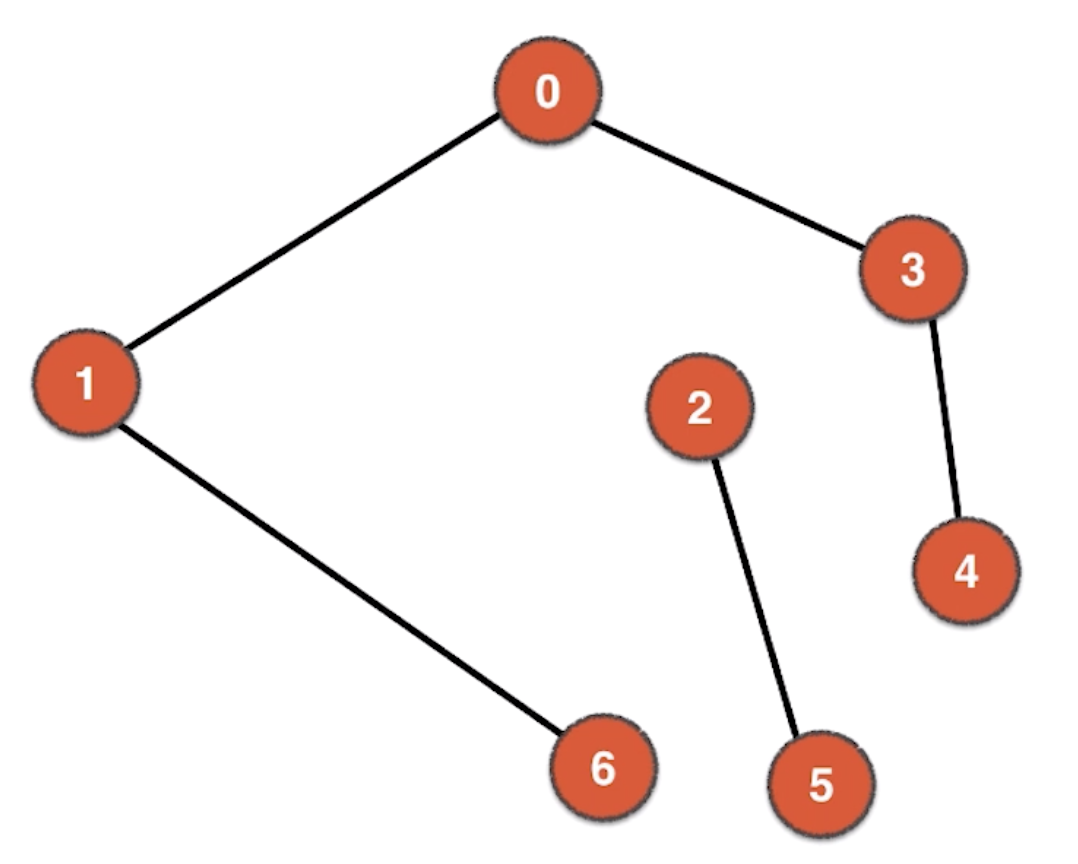
由上图可知，它是一个有2个联通分量的图，但可以肯定的是1个联通的无环图是树。

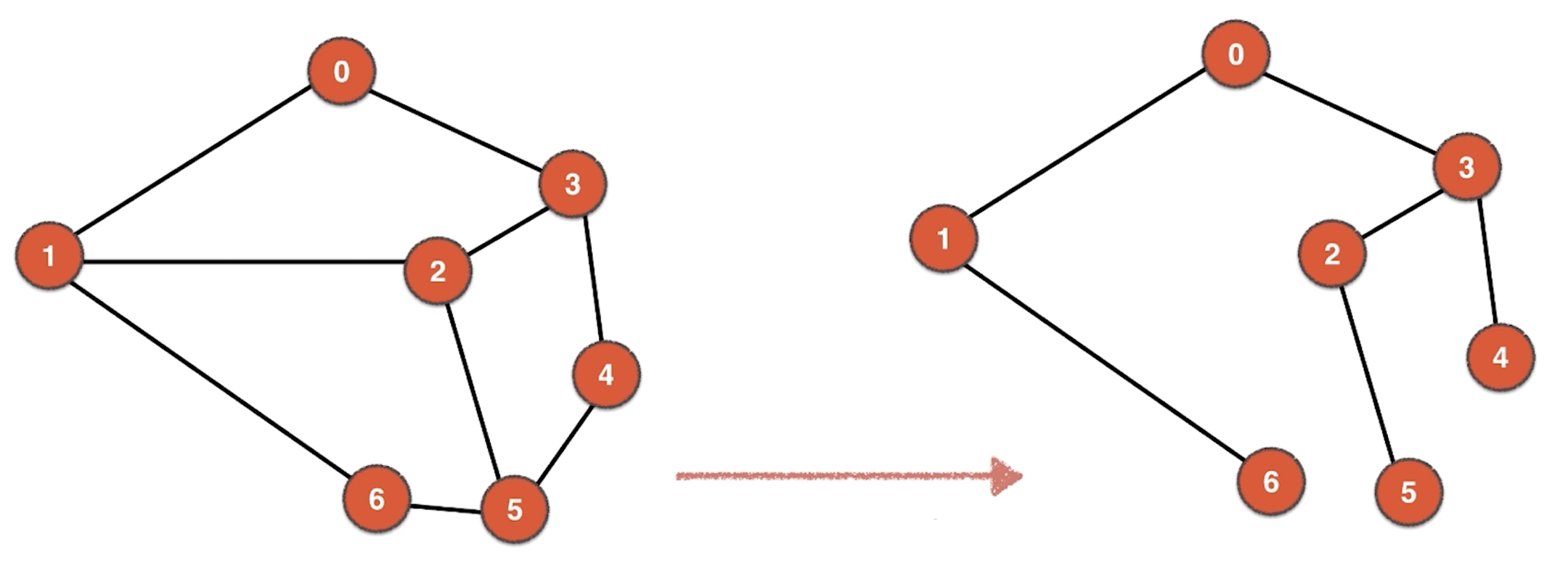
由该图我们可以看到，右边的图跟左边的图的顶点是一样的，区别只在于边，右边的图的边是左边的图的边的子集。我们将左边的图的一些边删除，就可以得到右边的图。同时右边的图还是一个树的形状。那么这个过程就可以称为联通图的生成树。由于树必须是联通的，所以只有联通图才有可能生成树。并且该生成树包含原联通图所有的顶点的树。这个树也是保障原联通图可以联通，并且边数最小的那个图，所以该树的边数为：V - 1，这里的V为顶点数。

但是反过来说，我们将一个联通图删边，包含所有的顶点，边数为V - 1,却不一定是联通图的生成树。如下面这个图，它就已经不再联通了，并且产生了环。

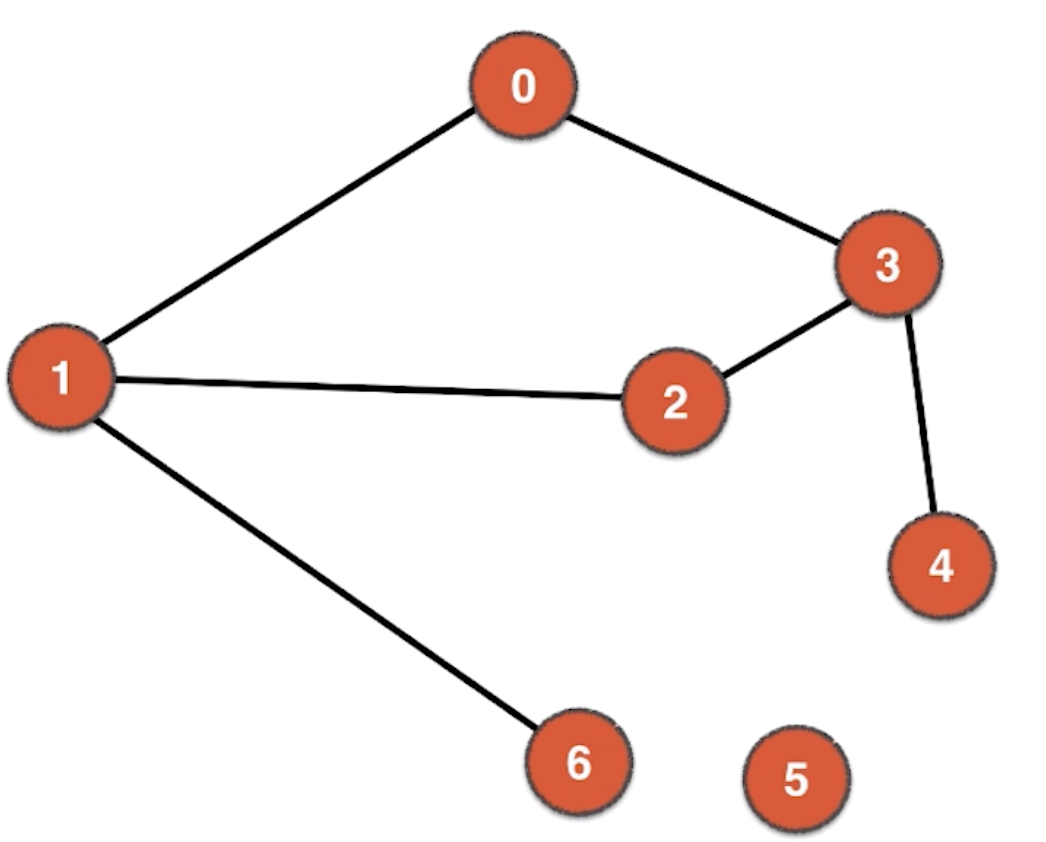
那么一个图不一定有生成树，这个图必须是一个联通的图。但是一个图一定有生成深林。一个联通图一定有生成树。对于不止一个联通分量的图，我们可以将各个联通分量生成树，进而获得生成森林。

在无向图中，一个顶点的度(degree)，就是这个顶点相邻的边数，这里也是在说简单图，不考虑自环边和平行边。但在一个有向图中，一个顶点的度的概念不同。所以我们可以看到下图中0这个顶点有两个邻边0-1、0-3，所以0这个顶点的度就是2.

无权无向图的邻接矩阵

接口

public interface Adj {
    int getV();
    int getE();

    /**
     * 是否存在某条边
     * @param v
     * @param w
     * @return
     */
    boolean hasEdge(int v,int w);

    /**
     * 获取和顶点相邻的边
     * @param v
     * @return
     */
    List<Integer> adj(int v);

    /**
     * 求一个顶点的度(顶点有多少个邻边)
     * @param v
     * @return
     */
    int degree(int v);
}

实现类

/**
 * 只支持处理简单图
 */
public class AdjMatrix implements Adj {
    //顶点数
    private int V;
    //边数
    private int E;
    //邻接矩阵
    private int[][] adj;

    public AdjMatrix(String filename) {
        File file = new File(filename);
        try (Scanner scanner = new Scanner(file)) {
            V = scanner.nextInt();
            if (V < 0) {
                throw new IllegalArgumentException("V必须为非负数");
            }
            adj = new int[V][V];
            E = scanner.nextInt();
            if (E < 0) {
                throw new IllegalArgumentException("E必须为非负数");
            }
            for (int i = 0;i < E;i++) {
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);
                if (a == b) {
                    throw new IllegalArgumentException("检测到自环边");
                }
                if (adj[a][b] == 1) {
                    throw new IllegalArgumentException("检测到平行边");
                }
                adj[a][b] = 1;
                adj[b][a] = 1;
            }
        }catch (IOException e) {
            e.printStackTrace();
        }
    }

    @Override
    public int getV() {
        return V;
    }

    @Override
    public int getE() {
        return E;
    }

    @Override
    public boolean hasEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return adj[v][w] == 1;
    }

    @Override
    public List<Integer> adj(int v) {
        validateVertex(v);
        List<Integer> res = new ArrayList<>();
        for (int i = 0;i < V;i++) {
            if (adj[v][i] == 1) {
                res.add(i);
            }
        }
        return res;
    }

    @Override
    public int degree(int v) {
        return adj(v).size();
    }

    private void validateVertex(int v) {
        if (v < 0 || v >= V) {
            throw new IllegalArgumentException("顶点" + v + "无效");
        }
    }

    @Override
    public String toString() {
        StringBuilder builder = new StringBuilder();
        builder.append(String.format("V = %d,E = %d\n",V,E));
        for (int i = 0;i < V;i++) {
            for (int j = 0;j < V;j++) {
                builder.append(String.format("%d ",adj[i][j]));
            }
            builder.append("\n");
        }
        return builder.toString();
    }

    public static void main(String[] args) {
        Adj adjMatrix = new AdjMatrix("/Users/admin/Downloads/g.txt");
        System.out.println(adjMatrix);
    }
}

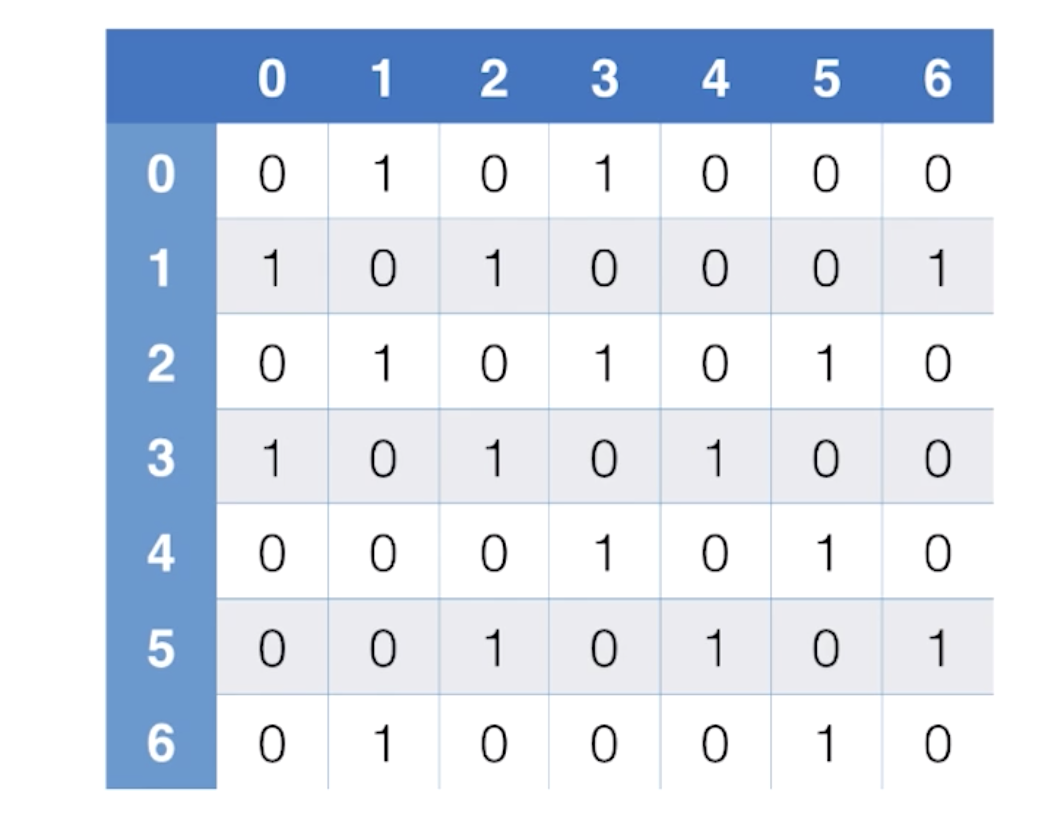
g.txt中的内容(第一行表示有7个顶点，9条边；第二行到最后表示哪个顶点与哪个顶点相连)

运行结果

V = 7,E = 9
0 1 0 1 0 0 0
1 0 1 0 0 0 1
0 1 0 1 0 1 0
1 0 1 0 1 0 0
0 0 0 1 0 1 0
0 0 1 0 1 0 1
0 1 0 0 0 1 0

时间复杂度和空间复杂度

空间复杂度 O(V^2)

时间复杂度

建图 O(E)

查看两个节点是否相邻 O(1)

求一个点的相邻节点 O(V)

无权无向图的邻接表

由于邻接矩阵的空间复杂度过大，我们使用邻接表来表示这个图

实现类

public class AdjList implements Adj {
    //顶点数
    private int V;
    //边数
    private int E;
    //邻接表
    private List<Integer>[] adj;

    @SuppressWarnings("unchecked")
    public AdjList(String filename) {
        File file = new File(filename);
        try (Scanner scanner = new Scanner(file)) {
            V = scanner.nextInt();
            if (V < 0) {
                throw new IllegalArgumentException("V必须为非负数");
            }
            adj = new LinkedList[V];
            for (int i = 0;i < V;i++) {
                adj[i] = new LinkedList<>();
            }
            E = scanner.nextInt();
            if (E < 0) {
                throw new IllegalArgumentException("E必须为非负数");
            }
            for (int i = 0;i < E;i++) {
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);
                if (a == b) {
                    throw new IllegalArgumentException("检测到自环边");
                }
                if (adj[a].contains(b)) {
                    throw new IllegalArgumentException("检测到平行边");
                }
                adj[a].add(b);
                adj[b].add(a);
            }
        }catch (IOException e) {
            e.printStackTrace();
        }
    }

    @Override
    public int getV() {
        return V;
    }

    @Override
    public int getE() {
        return E;
    }

    @Override
    public boolean hasEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return adj[v].contains(w);
    }

    @Override
    public List<Integer> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    @Override
    public int degree(int v) {
        return adj(v).size();
    }

    private void validateVertex(int v) {
        if (v < 0 || v >= V) {
            throw new IllegalArgumentException("顶点" + v + "无效");
        }
    }

    @Override
    public String toString() {
        StringBuilder builder = new StringBuilder();
        builder.append(String.format("V = %d,E = %d\n",V,E));
        for (int v = 0;v < V;v++) {
            builder.append(String.format("%d :",v));
            adj[v].stream().map(w -> String.format("%d ",w))
                    .forEach(builder::append);
            builder.append("\n");
        }
        return builder.toString();
    }

    public static void main(String[] args) {
        Adj adjList = new AdjList("/Users/admin/Downloads/g.txt");
        System.out.println(adjList);
    }
}

运行结果

V = 7,E = 9
0 :1 3
1 :0 2 6
2 :1 3 5
3 :0 2 4
4 :3 5
5 :2 4 6
6 :1 5

来源：oschina

链接：https://my.oschina.net/u/3768341/blog/3176084

标签

图论