矢量图形的绘制归根结底是任意多边形的绘制。
比如一个填充圆,就是取圆上许多的点依次连接并填充内部构成的图形,虽然人肉眼看到的还是"圆"形,但它却是实实在在的多边形构造的。
再比如说直线,其实也就是4边形,只不过它是一个又窄又长的内部被填充的4边形。
任意多边形是如何绘制于电脑屏幕的呢?
很显然"多边形扫描线填充算法"能很好的工作,当然,这个算法用在矢量图形处理上,细节上还需要有所改进。
特别是要注意到矢量图形绘制中有所谓的"奇偶填充规则","非零填充规则"等,我只说说"(nonzero fill)非零填充"
非零填充规则:
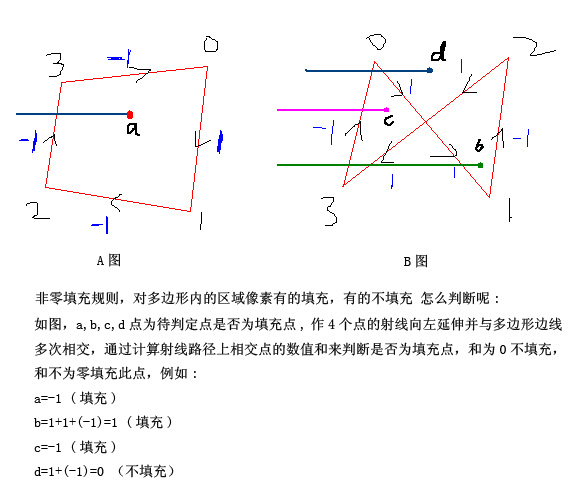
"非零填充规则"还有一个值得注意的方面是:边线方向的判断,就是图中多边形边线标识箭头以及+1,-1数字的规则。
A图B图中,绘图顺序为由0号点到1号点(0->1), 0号点的坐标y值比1号点的坐标y值小 ,所以标识数值为1。
绘图顺序为由3号点到0号点(3->0), 3号点的y值比0号点的y值大,所以标识数值为-1。
说到图形矢量,任意多边形又是如何被"矢量"起来的呢?
矢量起来的方法就是像素的 super sample aa(超级采样抗锯齿) 算法。(网上这个资料还是有的,这里就不详谈了-_-!!)
超采样绘制一个多边形,多边形的边缘就有了灰度渐变过度,这就矢量起来了.
这就是矢量图绘制的基础。
来源:https://www.cnblogs.com/cymheart/archive/2012/03/01/2374954.html