215. 数组中的第K个最大元素

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。
示例 1:
在这里插入图片描述
示例 2: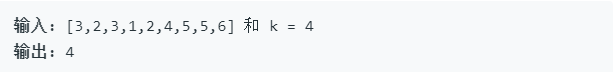

说明:
你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

2.方法一（快速排序）

利用快速排序的思想，对数组进行递减排序，把第k大的元素放到正确的位置。
算法过程：
1.利用partition()随机获取一个元素的下标index。
2.如果index > k-1，说明第k大元素在index的左边，right = index - 1。
2.如果index < k-1，说明第k大元素在index的右边，left = index + 1。
3.当index == k-1，退出循环，返回nums[index]。

3.代码

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int left = 0;
        int right = nums.size() - 1;
        int index = partition(nums,left,right);
        while(index != k-1){
            if(index > k-1){
                right = index - 1;
            }
            else{
                left = index + 1;
            }
            index = partition(nums,left,right);
        }
        return nums[index];
    }
    int partition(vector<int>& nums, int left, int right){
        int t = left;
        for(int i = left;i < right;++i){
            if(nums[i] > nums[right]){
                swap(nums[t++],nums[i]);
            }
        }
        swap(nums[t],nums[right]);
        return t;
    }
};

4.复杂度分析

时间复杂度：O(n)
空间复杂度：O(1)

5.方法2（最小堆）

最小堆堆顶元素top()的值最小，创建一个大小为k的最小堆，从遍历第k个元素开始遍历数组元素，如果nums[i] > top()，则删除top()，并且插入nums[i]，最小堆会自动更新；如果nums[i] < top()，则忽略。当遍历完数组元素时，堆里的元素时数组最大的k个元素。倒数第k大元素为top()。

6.代码

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        multiset<int,less<int>> min_heap;
        for(int i = 0;i < nums.size();++i){
            if(i < k){
                min_heap.insert(nums[i]);
            }
            else{
                auto top = min_heap.begin();
                if(nums[i] > *top){
                    min_heap.erase(top);
                    min_heap.insert(nums[i]);
                }
            }
        }
        return *min_heap.begin();
    }
};