Neural Networks: Learning
在给定训练集的情况下,为神经网络拟合参数的学习方法。
Cost function
Neural Network (Classification) 神经网络在分类问题中的应用
符号说明:
- \(L\) = total no. of layers in network 神经网络中的层数
- \(s_l\) = no. of units (not counting bias unit) in layer \(l\) 第\(l\)层的单元个数(偏置单元不计入内)
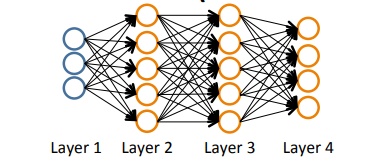
下图中的\(L = 4\), \(s_1 = 3\), \(s_2 = 5\), \(s_3 = 5\), \(s_4 = 4\).
Binary classification:
\(y = 0 or 1\) , 1 output unit. \(s_l = 1\).
Multi-class classification:
\(y \in R^K\), E.g. \(\left[ \begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix} \right]\),\(\left[ \begin{matrix} 0 \\ 1 \\ 0 \\ 0 \end{matrix} \right]\),\(\left[ \begin{matrix} 0 \\ 0 \\ 1 \\ 0 \end{matrix} \right]\),\(\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix} \right]\), \(K\) output units. \(s_l = K\).
综上:当只有两个类别时不需要使用一对多方法,\(K \geq 3\)时才会用。
Cost function
神经网络中的代价函数是逻辑回归里使用的代价函数的一般化形式。
Logistic regression:
\(J(\theta) = -\frac{1}{m}\left[ \sum_{i=1}^my^{(i)}log h_\theta(x^{(i)}) + (1-y^{(i)})log(1-h_\theta(x^{(i)})) \right] + \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2\)
Neural network:
\(h_\theta(x) \in R^K\), \((h_\theta(x))_i = i^{th}\) output
\(J(\theta) = -\frac{1}{m}\left[ \sum_{i=1}^m\sum_{k=1}^Ky_k^{(i)}log( h_\theta(x^{(i)}))_k + (1-y_k^{(i)})log(1-(h_\theta(x^{(i)}))_k) \right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}(\theta_{ji}^l)^2\)
其中\(m\)是特征值数目的个数,\(K\)是输出单元的数目个数,\(s_l\) 是第\(l\)层的单元数目,\(s_{l+1}\)是第\(l+1\)层的单元数目。\(\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}(\theta_{ji}^l)^2\)起的作用是将所有的\(i\)、\(j\)和\(l\)的\(\theta_{ij}\)的值都相加。
来源:https://www.cnblogs.com/songjy11611/p/12271527.html