什么是快慢指针

这种模式，有一个非常出门的名字，叫龟兔赛跑。咱们肯定都知道龟兔赛跑啦。但还是再解释一下快慢指针：这种算法的两个指针的在数组上（或是链表上，序列上）的移动速度不一样。还别说，这种方法在解决有环的链表和数组时特别有用。

通过控制指针不同的移动速度（比如在环形链表上），这种算法证明了他们肯定会相遇的。快的一个指针肯定会追上慢的一个（可以想象成跑道上面跑得快的人套圈跑得慢的人）。

咋知道需要用快慢指针模式？

那啥时候用快慢指针而不是上面的双指针呢？

一般情况下，快慢指针出现在链表的频率更高。

快慢指针判断链表有环

快指针fast一次走两步，慢指针slow一次走一步，如果有环的话，它们在环上一定会相遇（值相等），此时就证明有环。所以，如果最终fast == nullptr，那么判断链表无环；如果最终fast == slow，且fast != nullptr，那么链表有环。

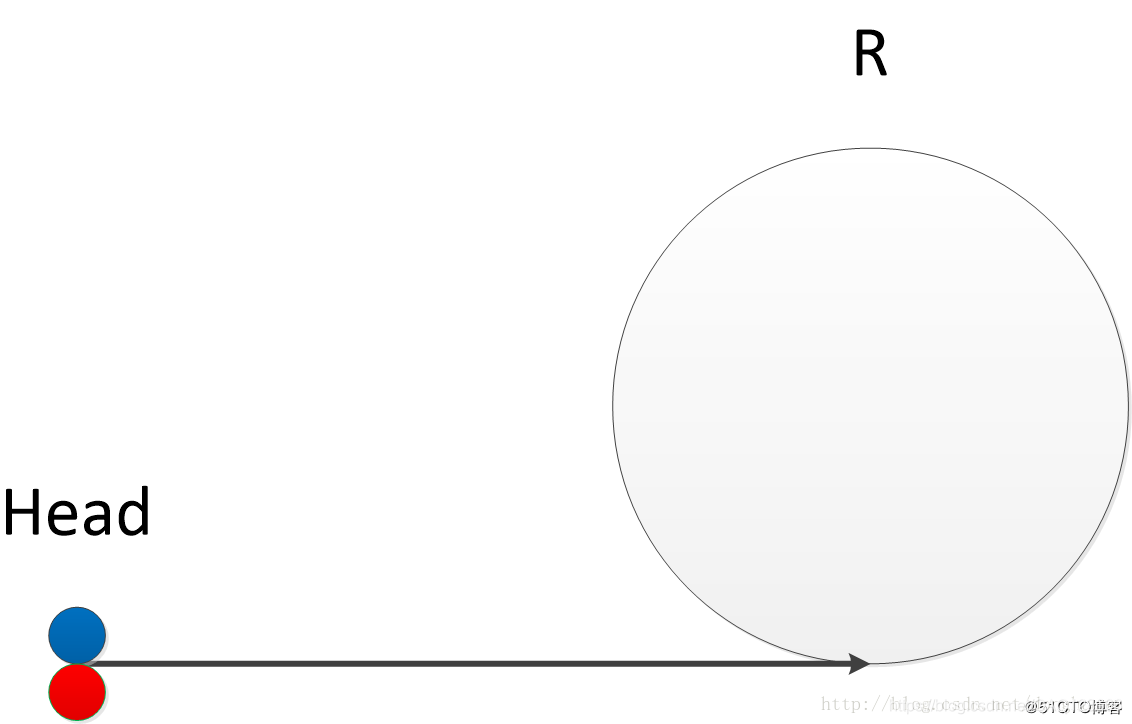
第一步：快慢指针从头结点出发。如下图所示。蓝色表示快指针fast，红色表示慢指针slow。
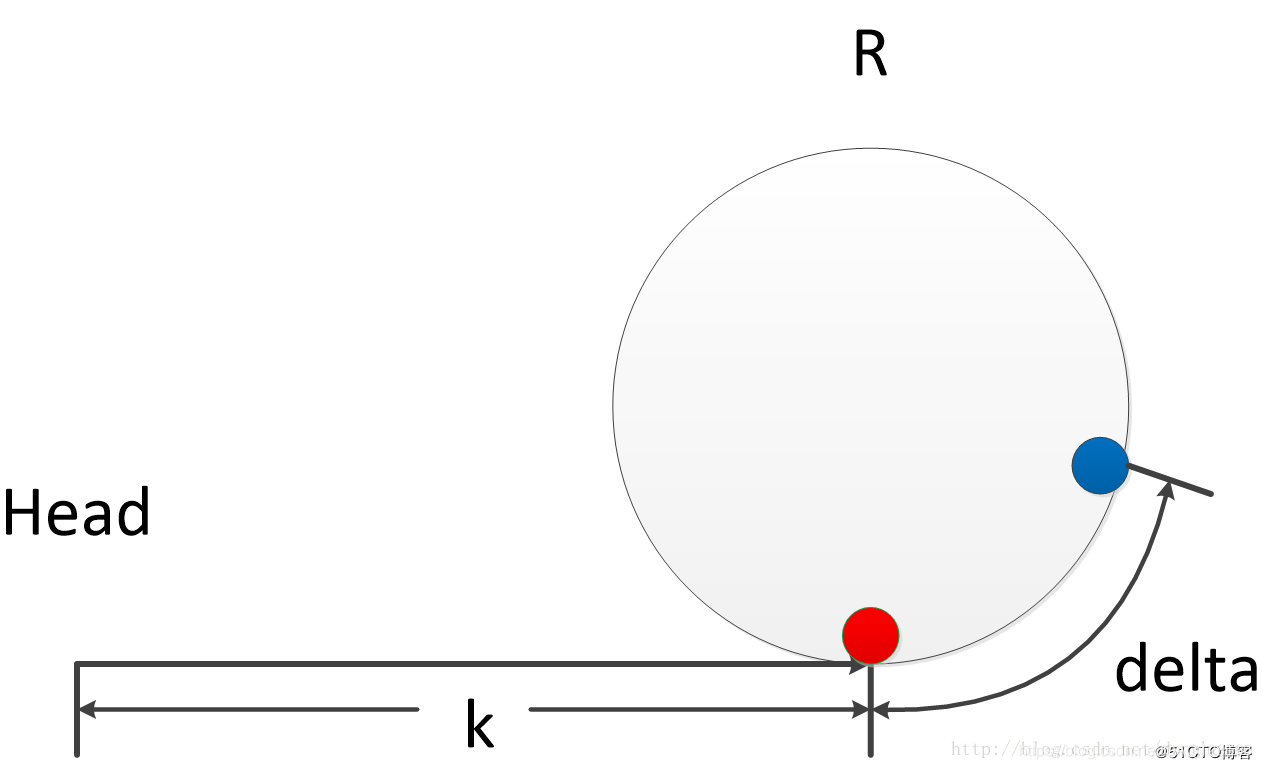
第二步：慢指针slow走到了环入口，共走了k步。此时快指针fast越过了环入口的步数为delta。因为快指针可能绕着环走了很多圈，快指针走了k + delta + n * R步，慢指针走了k步，又因为快指针走的步数是慢指针的两倍，所以k + delta + n * R = 2k，所以有k == delta + n * R。其中R为环的大小，n为快指针绕环走的步数。
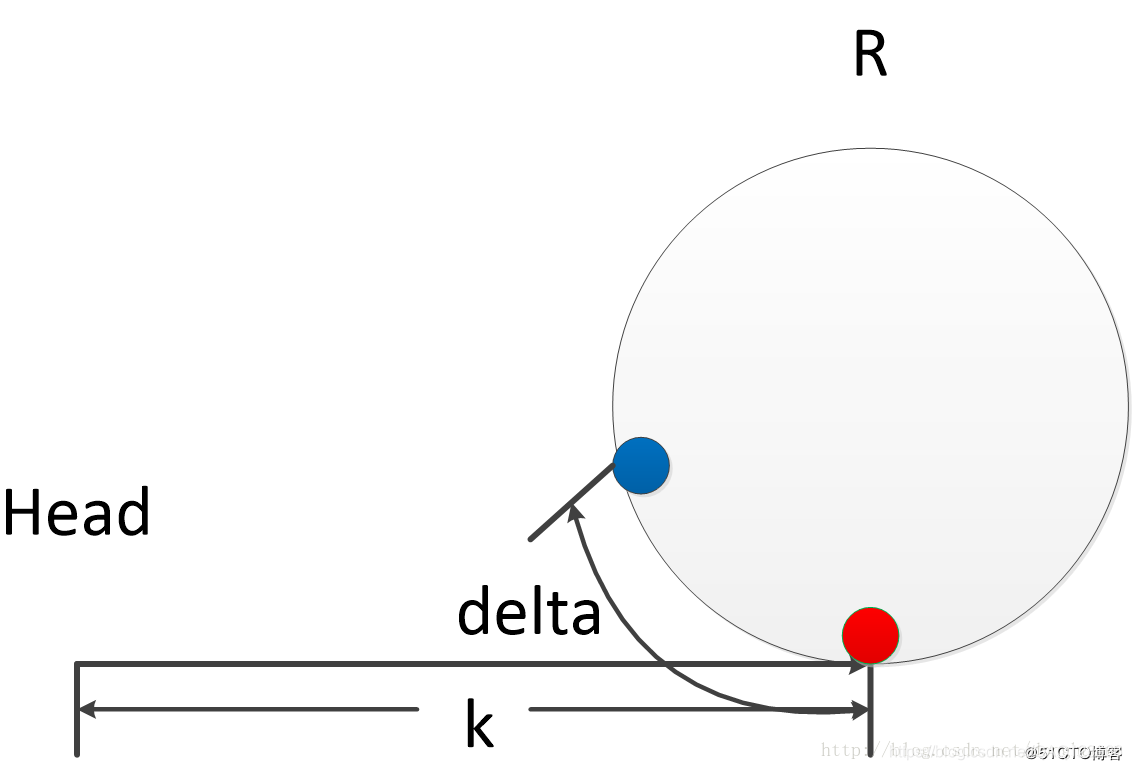
第三步：计算快慢指针相遇位置。因为慢指针在刚进入环时距离快指针delta步，所以快指针还需要比慢指针多走R - delta步才能与慢指针相遇。又因为快指针每次走两步，所以快指针还需要走2(R - delta)步。那么，相遇位置为2(R - delta) + delta == 2R - delta，即，距离环入口delta处，与慢指针刚进入环时快指针所在位置对称。
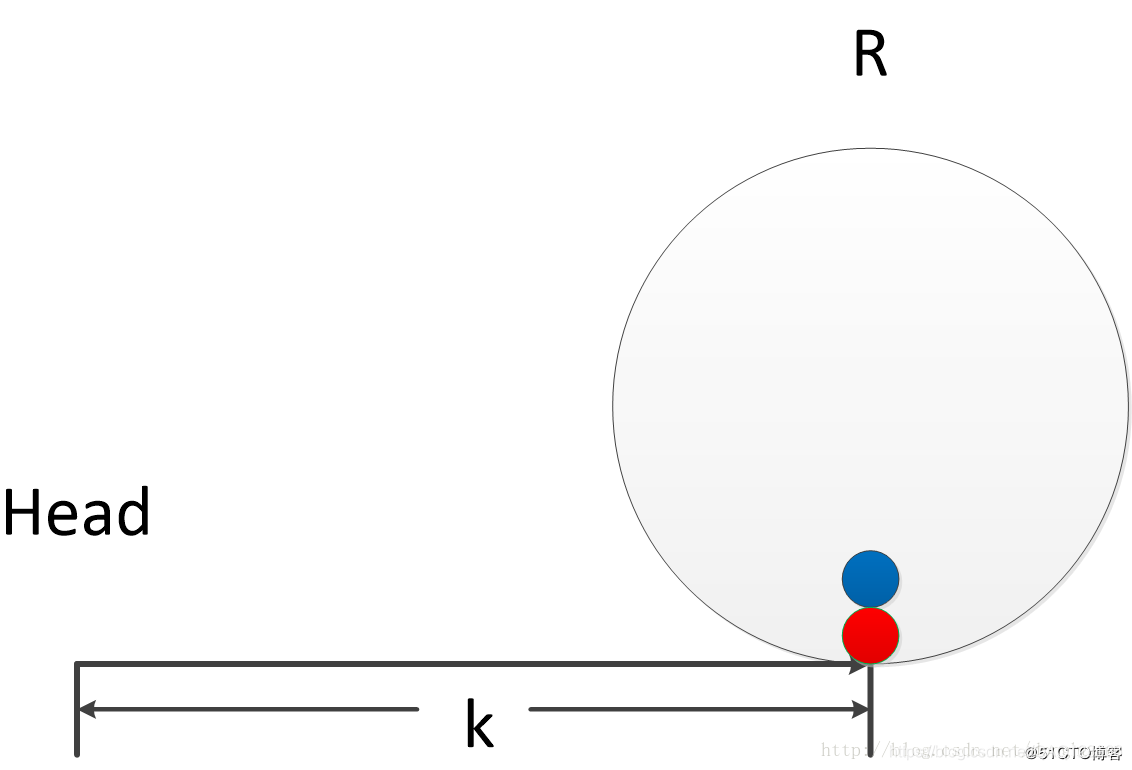
第四步：快指针重新从头结点开始走，速度为一次一步，与慢指针相同；慢指针在原位置走，一次一步。可知，快指针走到环入口时，所需步数为k。刚好，k == delta + n * R，这也是慢指针在环中所走的距离。此时快慢指针在环入口相遇。