大数据科学计算基础算法部分复习（1）-----亚线性空间算法

亚线性空间算法

Q1近似计数问题：

直观思想:
就是把原先的数利用概率压缩存储。比如一个出现了2⁹次的数a_i，如果表示为2的9次方会很占地方，因此就记9，而每出现一次就有1/2ⁱ的可能加一，若出现了2ⁱ次必定+1，那么最终统计看实际出现此处就用记录的数字k，算2^k-1即可。
为什么要-1，可能是为了出现0次的时候可以算出来是0吧，即为了求均值等于实际值。

• Morris算法就是最原始的，即上述直观思想的算法实现。
• Morris+ 就是跑k个之后取k个的平均值。
• Morris++ 就是跑m次后用median技术取中值。

Q2不重复元素数目。

直观思想:
假设哈希之后就是均匀的分布在0-1上了，那么有n个的话，最小的就是1/n了，因此就是最终返回1/z - 1，我理解这个减1，就是因为初始z是1。

• FM算法就是这样最原始的。
• FM+算法就是运行q次后取平均值。
• FM’+ (Bottom-k)算法看不懂，但意思就是维护前k个最小值，完了最终估计k/zk个不一样的数字。
• FM++就是利用median技术，运行t次去中位数。
• 朴实（实用？）FM算法，它的直观思想（我认为）是先假设hash后均匀分布，012345678.然后根据二进制0的个数的最大值z，来估计不重复元素数目。最后输出的是2z+1/2.但是注意其中的hash函数.然后可以还用Median技术来降低方差。

BJKST算法
这个算法的直观思想就是，假定经初始h函数哈希之后会使得这些不重复元素平均分布，然后维护一个桶B,假定有d个不同元素，期望有d/2z能落入桶中，这样|B| * 2z就是对d的估计。
但是B应该有个上限，否则仍然不是亚线性算法。

Q3频度估计和点查询

Misra-Gries算法非常直观，维护一个有上限的map，未达到上限时正常操作，当超出上限后，将集合中每个键的值-1，然后删掉为0的元素。（好像是直到空出来地方？）
因为只有减去，所以查询结果只能小，不会大。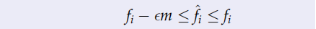

Metwally算法同样非常直观，维护一个有上限的map，未达到上限时正常操作，当超出上限后，将集合中最小元素的键的值即为min，然后给删掉它，给新来的键的值变成min+1。
最后的效果就是总量的出现次数不变
这个也很好理解，只有增加没有减去。

计数最小略图跳过了。TODO。

Q4频度矩估计

Basic AMS算法，其思想就是随机在流中抽取一个元素，然后开始计此后该元素的频数。至于具体伪代码的意思我理解的不太准确。

AMS无法直接用median，只能先用平均降下方差再用median。

Q6固定大小采样

水库抽样算法在概率论的思想下比较直观，就是利用了条件概率，使得可以扫一次就能抽样出s个样本了。

每次新来的都有s/m+1即，样本总数/流总长度 的概率被抽中，原来里面样本的将以等可能的概率被移出去。

Q7 Bloom Filter

感觉也是比较容易想出来的。
主要是利用了hash函数，我认为最主要的设计思路就是用了hash桶的设计理念.然后尽可能缩小错误的可能。更详细的思想需要可以自行百度。

来源：CSDN

作者：一个即将拥有腹肌的少年

链接：https://blog.csdn.net/weixin_42461322/article/details/104029190