动态规划

参考视频av16544031、av18512769

一、重叠子问题

问题1

回顾斐波那契数列，实质是一个递归关系

也是一个overlap sub-problem 重叠子问题

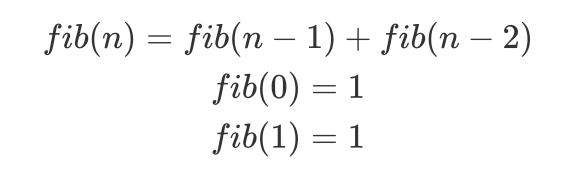
如果我们要计算fib(7)，就会去计算fib(6)和fib(5)，之后继续往下，中间fib(6)分解成fib(5)和fib(4)，在这部分，我们的fib进行了很多次分解，fib(5)被计算了2次。

算法复杂度会变成O(2^n)

解决方案

将重叠子问题进行保存起来，然后之后再进行取用

二、最优解

问题2

我们有8个task，然后我们中间有重合的时间段，每个task会有一定的收益，怎样才能让收益最高？这是一个典型的dp问题。

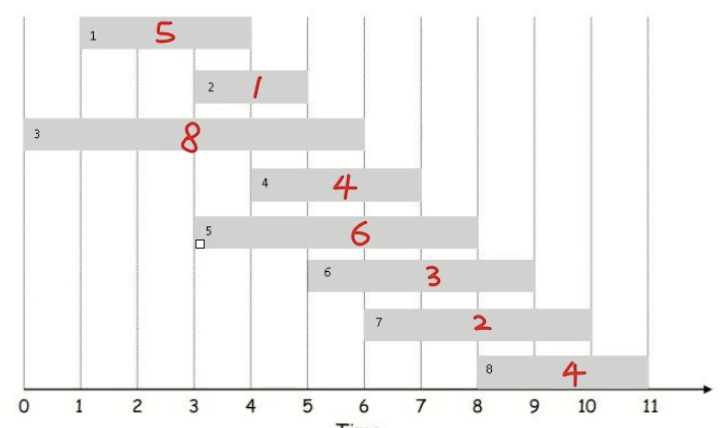
解决方案

OPT(optimizations) 最优解

要获得opt，首先得需要思考进行选和不选问题。

If OPT(8) 选择：4+OPT(5) 不选择：OPT(7)

以此类推，我们就可以知道一张prev表

问题3

我们有如下数字，选出一堆数字，使得不相邻，且加起来结果最大。

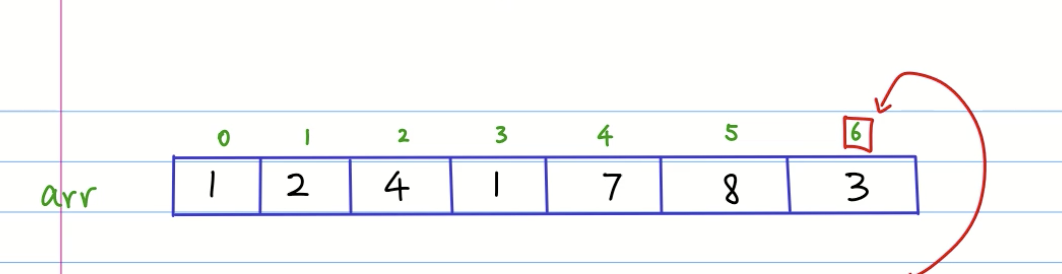
解决方案

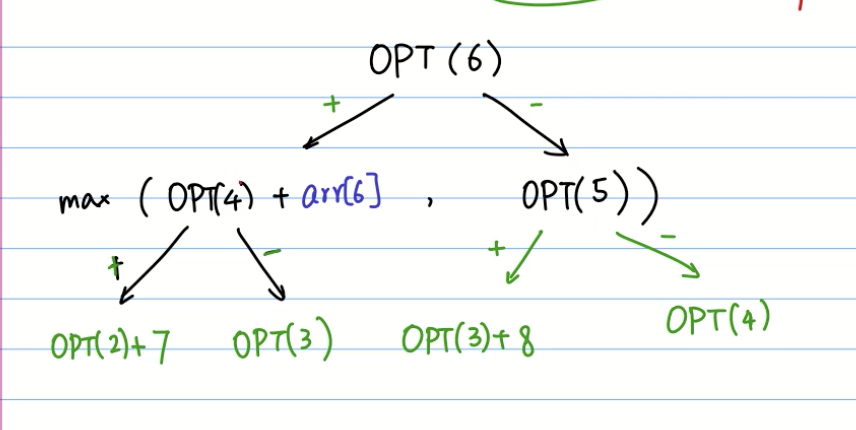
javascript代码：

var arr = [1,2,4,1,7,8,3]
var max = (a,b) => a > b ? a:b
var rec_opt = (arr,i)=>{
    if(i===0) return arr[0]
    else if(i===1) return max(arr[0],arr[1])
    else{
        var A = rec_opt(arr,i-2) + arr[i]
        var B = rec_opt(arr,i-1) 
        return max(A,B)
    }
}

var dp_opt = (arr)=>{
    var opt = [0,0,0,0,0,0,0]
    opt[0] = arr[0]
    opt[1] = max(arr[0],arr[1])
    for(let i = 2;i < arr.length;i++){
        var A = opt[i-2] + arr[i]
        var B = opt[i-1]
        opt[i] = max(A,B)
    }
    return opt[ arr.length - 1 ];
}

console.log(rec_opt(arr))
console.log(dp_opt(arr))

三、子集问题

Subset问题

问题4

有无一个方案，在arr中选出n个数字与s一样的，如果没有，打印false

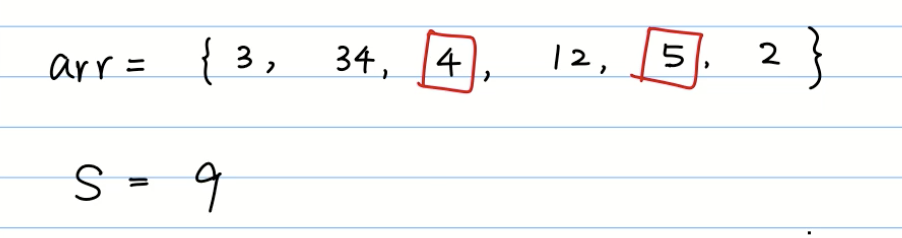
解决方案

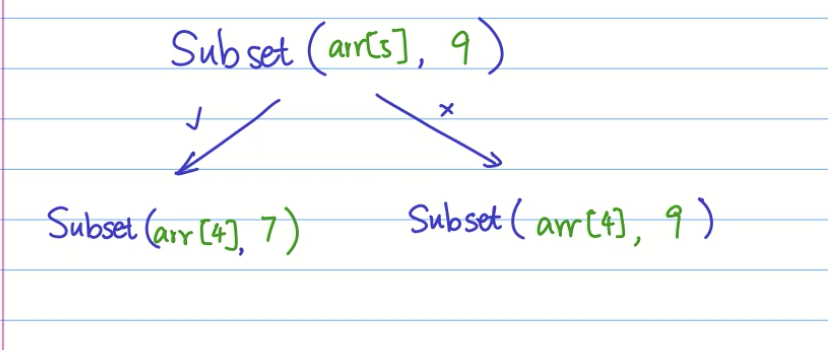
JavaScript代码

arr = [3,34,4,12,5,2]

var rec_subset = (arr,i,s)=>{
    if(s === 0) return true
    else if(i === 0) return arr[0] === s
    else if(arr[i] > s) return rec_subset(arr,i-1,s)
    else{
        var A = rec_subset(arr,i-1,s-arr[i])
        var B = rec_subset(arr,i-1,s)
        return A||B
    }
}

console.log(rec_subset(arr,arr.length-1,9))
console.log(rec_subset(arr,arr.length-1,10))
console.log(rec_subset(arr,arr.length-1,11))
console.log(rec_subset(arr,arr.length-1,12))
console.log(rec_subset(arr,arr.length-1,13))

四、总结

看了灯神的dp，很清晰，讲的很牛。dp在分析问题的时候，确实是一个比较重要的方法，以空间换时间，来寻求更高效率。

来源：https://www.cnblogs.com/littlepage/p/12219884.html

标签

动态规划算法

arr

var