IQ调制器

IQ调制就是数据分为两路，分别进行载波调制，两路载波相互正交。I是in-phase（同相）, q是 quadrature（正交）。
IQ调制是矢量的方向问题，同相就是矢量方向相同的信号；正交分量就是两个信号矢量正交（差90°）；IQ信号是一路是0°或180°，另一路是90°或270°，叫做I路和Q路，它们就是两路正交的信号。
因为I和Q是在相位上面正交的（不相干），可以作为两路信号看待。所以频谱利用率比单相调制提高一倍。但是IQ对解调要求高于单相（必须严格与I相差90度的整数倍，否则Q信号会混进I，I也会混进Q）。
简单的说就是数据分为两路，分别进行载波调制，两路载波相互正交。 正交信号就是两路频率相同，相位相差90度的载波，一般用sin和cos，与I，Q两路信号分别调制后一起发射，从而提高频谱利用率。
举例说明：
$x_c(t)=x_R(t)A_ccos(2\pi f_ct+\theta)+x_L(t)A_csin(2\pi f_ct+\theta)$
写成复数形式(把$cosx$写成$e^{ix}$，把$sinx$写成$-ie^{ix}$，总之就是复数的实部就是对应的实数)就是：
$\mathring{x_c(t)}=A_c(x_R(t)-ix_L(t))e^{i(2\pi f_ct+\theta)}$
写成包络就是：
$\widetilde{x_c(t)}=A_c(x_R(t)-ix_L(t))e^{i\theta}$
那么在接收端应该如何解调出$x_R(t)$和$x_L(t)$呢？
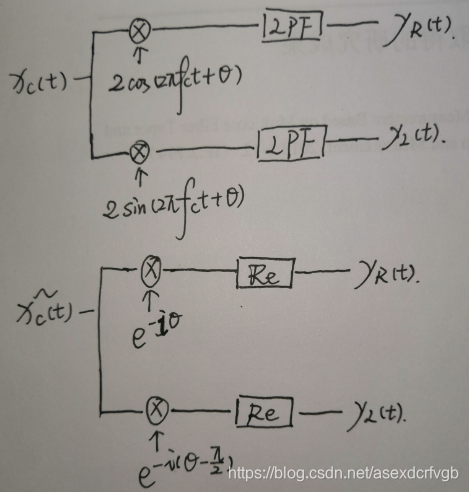
在接收端将原始信号分别乘以$2cos(2\pi f_ct+\theta)$和$2sin(2\pi f_ct+\theta)$
$x_c(t)\times 2cos(2\pi f_c+\theta)=(x_R(t)A_ccos(2\pi f_ct+\theta)+x_L(t)A_csin(2\pi f_ct+\theta))\times 2cos(2\pi f_c+\theta)=x_R(t)A_c(cos(4\pi f_ct)+cos(\theta -\theta))+x_L(t)A_c(sin(4\pi f_ct)+sin(\theta -\theta))$
通过低通滤波器滤除$4\pi f_c$频段后，上式等于$A_cx_R(t)$
$x_c(t)\times 2sin(2\pi f_c+\theta)=(x_R(t)A_ccos(2\pi f_ct+\theta)+x_L(t)A_csin(2\pi f_ct+\theta))\times 2sin(2\pi f_c+\theta)=x_R(t)A_c(sin(4\pi f_ct)-sin(\theta -\theta))+x_L(t)A_c(-cos(4\pi f_ct)+cos(\theta -\theta))$
通过低通滤波器滤除$4\pi f_c$频段后，上式等于$A_cx_L(t)$
也可以通过包络来分析，将包络分别乘以$e^{-i\theta}$和$e^{-i(\theta -\frac{\pi}{2})}$
$Re\{\widetilde{x_c(t)}\times e^{-i\theta}\}=Re\{A_c(x_R(t)-ix_L(t))\}=A_cx_R(t)$
$Re\{\widetilde{x_c(t)}\times e^{-i(\theta-\frac{\pi}{2})}\}=Re\{A_c(x_R(t)-ix_L(t))e^{i\frac{\pi}{2}}\}=Re\{A_c(x_R(t)-ix_L(t))\times i\}=Re\{A_c(x_L(t)+ix_R(t))\}=A_cx_L(t)$

来源：CSDN

作者：tangerinee

链接：https://blog.csdn.net/asexdcrfvgb/article/details/104022304