以下资料参考自Owen_codeisking大佬的博客
一、\(CDQ\)分治
首先，建议各位小盆友先前置一下树状数组和分治的知识
1.二维偏序
二维偏序问题：给你\(n\)个点，以及这\(n\)个点坐标\(X_{i}\)和\(Y_{i}\)，令\(F{i}=X{j}\le X{i}且Y{j}\le Y{i}\)的点的个数，求\(F{i}\)
这一看，当然可以用暴力解法，最暴力的可以达到\(O(n^2)\)的时间复杂度，但只能在\(n\le5000\)时用
但如果\(10000\le n\)呢？
或许您有\(n^2\)过百万的经历（那是因为您是大佬），但下面我们就介绍一种\(O(nlogn)\)的算法：\(CDQ\)分治最基础的运用
我们把这个问题看成一张图（偷来的）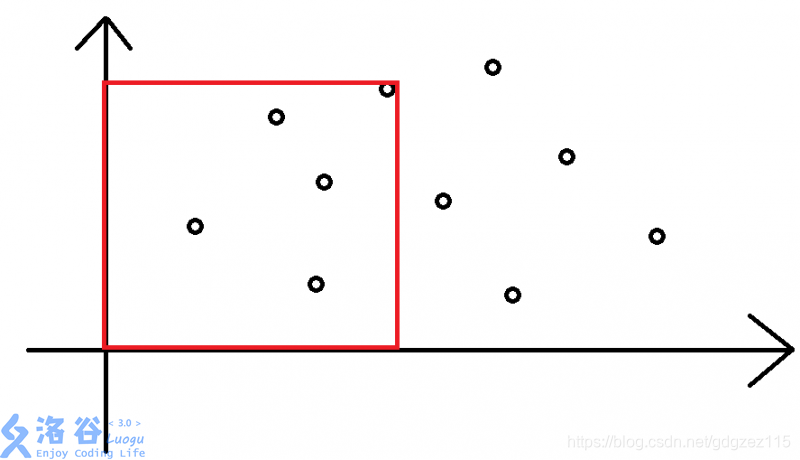
那么，图中被圈起来的点就是对于矩形右上角满足条件的点
首先，我们先将点的纵坐标\(y{i}\)从小到大排序（排序横坐标还是纵坐标看心情（随便）），这个用一个\(sort\)就可以实现
接着，我们保证了\(y{i}\)的从小到大后，就开始对横坐标进行排序
这个排序操作可以用树状数组实现
int c[N];
void add(int x,int y)
{
for(;x<=N;x+=lowbit(x))c[x]+=y;
}
int sum(int x)
{
int ans=0;
for(;x>0;x-=lowbit(x))ans+=c[x];
return ans;
}
这就是树状数组模板，不多讲
#include<bits/stdc++.h>
using namespace std;
# define lowbit(x) ((x)&(-(x)))
# define int long long
const int N=100010;
int n;
struct edge
{
int a,b;
}p[N];
int c[N];
bool cmp(edge a,edge b)
{
if(a.a==b.a)return a.b<b.b;
return a.a<b.a;
}
int sum(int x)//从大往小搜索
{
int ans=0;
for(;x;x-=lowbit(x))ans+=c[x];
return ans;
}
void add(int x,int y)
{
for(;x<N;x+=lowbit(x))c[x]+=y;
}
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)scanf("%lld %lld",&p[i].a,&p[i].b);
sort(p+1,p+n+1,cmp);
int ans=0;
for(int i=1;i<=n;i++)
{
int now=sum(p[i].b+1);//这就是f[i]的值
ans+=now;
add(p[i].b+1,1);
}
printf("%lld",ans);
return 0;
}
2.三维偏序
这个就是在二维偏序上多加一维，从原来条件的\(X{j}\le X{i}且Y{j}\le Y{i}\)增加到\(X{j}\le X{i}且Y{j}\le Y{i}且Z{j}\le Z{i}\)
这时，我们还是先按横坐标排序，满足第一维条件
然后，我们用归并排序满足第二维条件
再用树状数组，满足第三维条件
这里我们就来详细看看归并排序
我们在归并时，考虑对于区间\([l,mid]\)对区间\([mid+1,r]\)贡献，因为我们已经通过排序满足了第一维条件，所以不论怎么打散，\([l,mid]\)区间的所有数都是小于等于\([mid+1,r]\)的数的
我们首先设一个结构体
struct edge
{
int a,b,c,re,ans;//re表示与e[i]重复的点的个数，ans表示对于i满足条件的节点个数
}e[N],t[N];
归并，顾名思义，递归排序合并，因此，归并需要靠递归实现。
if(l==r)return ;
int mid=(l+r)>>1;
cdq(l,mid);cdq(mid+1,r);
相信以上代码很好理解
重难点:敲黑板
接着，我们需要分别遍历区间\([l,mid]\)和区间\([mid+1,r]\)中的数并且相互比较
我们令区间\([l,mid]\)中遍历到的点为\(p\)，区间\([mid+1,r]\)中的为\(q\)，在设一个结构体\(t\)存储更改过顺序的点。
- 如果\(p\)的第二维小于等于\(q\)中的第二维
那么第一维和第二维都满足了，则直接树状数组满足第三维，更新\(t\)，且继续遍历下一个\(p\) - 如果不满足上一个条件，则将\(ans\)更新，加上对于\(q\)满足条件的节点的个数，并且更新\(t\)，且继续遍历下一个\(q\)
while(p<=mid&&q<=r)
{
if(e[p].b<=e[q].b)add(e[p].c,e[p].re),t[tot++]=e[p++];
else e[q].ans+=sum(e[q].c),t[tot++]=e[q++];
}
在\(while\)结束后，担心还有点没有遍历到，于是要从当前的\(p\)遍历到\(mid\)，从\(mid+1\)到\(q\)，操作都与上面代码相同
while(p<=mid)add(e[p].c,e[p].re),t[tot++]=e[p++];
while(q<=r)e[q].ans+=sum(e[q].c),t[tot++]=e[q++];
最后还原树状数组，因为我们只是为了更新\(t\)数组，为了之后的操作实现，需要还原
并将\(t\)复制给当前结构体
for(int i=l;i<=mid;i++)add(e[i].c,-e[i].re);
for(int i=l;i<=r;i++)e[i]=t[i];
整代码（我知道你们只看这个）
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-(x)))
#define N 100010
using namespace std;
int n,m;
int output[N];
int c[N];
struct edge
{
int a,b,c,re,ans;
}e[N],t[N];
bool cmp(edge a,edge b)
{
if(a.a!=b.a)return a.a<b.a;
if(a.b!=b.b)return a.b<b.b;
return a.c<b.c;
}
void add(int x,int y)
{
for(;x<=m;x+=lowbit(x))c[x]+=y;
}
int sum(int x)
{
int ans=0;
for(;x;x-=lowbit(x))ans+=c[x];
return ans;
}
void cdq(int l,int r)
{
if(l==r)return ;
int mid=(l+r)>>1;
cdq(l,mid);cdq(mid+1,r);
int p=l,q=mid+1,tot=l;
while(p<=mid&&q<=r)
{
if(e[p].b<=e[q].b)add(e[p].c,e[p].re),t[tot++]=e[p++];
else e[q].ans+=sum(e[q].c),t[tot++]=e[q++];
}
while(p<=mid)add(e[p].c,e[p].re),t[tot++]=e[p++];
while(q<=r)e[q].ans+=sum(e[q].c),t[tot++]=e[q++];
for(int i=l;i<=mid;i++)add(e[i].c,-e[i].re);
for(int i=l;i<=r;i++)e[i]=t[i];
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d %d %d",&e[i].a,&e[i].b,&e[i].c);
e[i].re=1;
}
sort(e+1,e+n+1,cmp);
int cnt=1;
for(int i=2;i<=n;i++)
{
if(e[cnt].a==e[i].a&&e[cnt].b==e[i].b&&e[cnt].c==e[i].c)e[cnt].re++;
else e[++cnt]=e[i];
}
cdq(1,cnt);
for(int i=1;i<=cnt;i++)output[e[i].ans+e[i].re-1]+=e[i].re;
for(int i=0;i<n;i++)printf("%d\n",output[i]);
return 0;
}
tips：因为在P3810 【模板】三维偏序（陌上花开），有可能出现重复的点，所以需要判重
- 四维偏序
太变态了，蒟蒻暂时还不会，想了解的可以看看博客顶的参考博客