Splay大法是坠吼滴!
1552: [Cerc2007]robotic sort
Time Limit: 5 Sec Memory Limit: 64 MB
Submit: 436 Solved: 186
[Submit][Status][Discuss]Description
Input
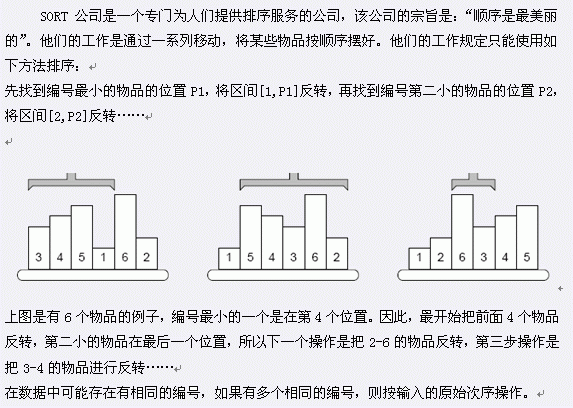
输入共两行,第一行为一个整数N,N表示物品的个数,1<=N<=100000。第二行为N个用空格隔开的正整数,表示N个物品最初排列的编号。Output
输出共一行,N个用空格隔开的正整数P1,P2,P3…Pn,(1 < = Pi < = N),Pi表示第i次操作前第i小的物品所在的位置。 注意:如果第i次操作前,第i小的物品己经在正确的位置Pi上,我们将区间[Pi,Pi]反转(单个物品)。Sample Input
6
3 4 5 1 6 2Sample Output
4 6 4 5 6 6HINT
Source
还算水的一道区间维护题目, 操作涉及区间翻转所以要用无旋 $Treap$ 或者$Splay$ .
主要思路是每次先建出这棵平衡树, 维护以结点为根的子树的大小, 最小值和最小值所在的子树(左/右/根), 然后每次根据保存的最小值的位置去查找并根据子树大小计算它所在的下标. 然后每次找到之后将其作为区间右端点, 左端点由于是顺序的所以直接从 $1$ 到 $n$ 枚举, 将这个选定的区间翻转即可. 翻转后这个最小值会对后面的计算产生额外影响所以要将已经排好序的结点的值重置为 $\infty$ 并向上更新.
以及题目要求该排序必须做到稳定, 所以我们保存数据时可以使用 $std::pair$, 第一关键字为键值, 第二关键字为该键值初始时的下标.
虚拟结点为了防止干扰答案 (本题中求最小值是针对整棵树, 而不像某维修数列全是指定区间结果虚拟结点一直在待求值的子树外) 键值与最小值均为 $\infty$,
然后就是注意没事多写几个标记下传操作, 标记下传多了顶多让你常数大点, 但下传少了可是会出人命的...
还有Splay的时候判根要判 $prt$ 是否等于传入的第二个参数而不是直接和 $NULL$ 比较(被坑), Splay内部的旋转要么以 $prt$ 为转轴要么以 $prt$ 的 $prt$ 为转轴, 不要脑抽写成以本结点为转轴 (又被坑了我好菜啊)
参考代码如下:

1 #include <vector>
2 #include <cstdio>
3 #include <cstring>
4 #include <cstdlib>
5 #include <iostream>
6 #include <algorithm>
7
8 #define lch chd[0]
9 #define rch chd[1]
10 #define kch chd[k]
11 #define xch chd[k^1]
12
13 const int INF=0x7FFFFFFF;
14 typedef std::pair<int,int> pr;
15
16 class SplayTree{
17 private:
18 struct Node{
19 pr k;
20 int s;
21 pr m;
22 int mp;
23 bool rev;
24 Node* prt;
25 Node* chd[2];
26 Node(const pr& key){
27 this->s=1;
28 this->mp=-1;
29 this->k=key;
30 this->m=key;
31 this->prt=NULL;
32 this->lch=NULL;
33 this->rch=NULL;
34 this->rev=false;
35 }
36 ~Node(){
37 delete this->lch;
38 delete this->rch;
39 }
40 inline void Flip(){
41 if(this==NULL)
42 return;
43 this->rev=!this->rev;
44 std::swap(this->lch,this->rch);
45 if(this->mp!=-1)
46 this->mp^=1;
47 }
48 inline void PushDown(){
49 if(this!=NULL&&this->rev){
50 this->lch->Flip();
51 this->rch->Flip();
52 this->rev=false;
53 }
54 }
55 inline void Maintain(){
56 if(this!=NULL){
57 this->s=this->lch->size()+this->rch->size()+1;
58 this->m=this->k;
59 this->mp=-1;
60 if(this->lch->min()<this->m){
61 this->m=this->lch->min();
62 this->mp=0;
63 }
64 if(this->rch->min()<this->m){
65 this->m=this->rch->min();
66 this->mp=1;
67 }
68 }
69 }
70 inline pr min(){
71 return this==NULL?std::make_pair(INF,INF):this->m;
72 }
73 inline int minp(){
74 return this==NULL?-1:this->mp;
75 }
76 inline int size(){
77 return this==NULL?0:this->s;
78 }
79 inline pr key(){
80 return this==NULL?std::make_pair(INF,INF):this->k;
81 }
82 }*root;
83 void Rotate(Node* root,int k){
84 Node* tmp=root->xch;
85 root->PushDown();
86 tmp->PushDown();
87 tmp->prt=root->prt;
88 if(root->prt==NULL)
89 this->root=tmp;
90 else if(root->prt->lch==root)
91 root->prt->lch=tmp;
92 else
93 root->prt->rch=tmp;
94 root->xch=tmp->kch;
95 if(root->xch!=NULL)
96 root->xch->prt=root;
97 tmp->kch=root;
98 root->prt=tmp;
99 root->Maintain();
100 tmp->Maintain();
101 }
102 void Splay(Node* root,Node* prt=NULL){
103 while(root->prt!=prt){
104 int k=root->prt->lch==root;
105 if(root->prt->prt==prt)
106 Rotate(root->prt,k);
107 else{
108 int d=root->prt->prt->lch==root->prt;
109 Rotate(k==d?root->prt->prt:root->prt,k);
110 Rotate(root->prt,d);
111 }
112 }
113 }
114 Node* Build(const std::vector<pr>& v,int l,int r){
115 if(l>r)
116 return NULL;
117 int mid=(l+r)>>1;
118 Node* tmp=new Node(v[mid]);
119 tmp->lch=Build(v,l,mid-1);
120 if(tmp->lch!=NULL)
121 tmp->lch->prt=tmp;
122 tmp->rch=Build(v,mid+1,r);
123 if(tmp->rch!=NULL)
124 tmp->rch->prt=tmp;
125 tmp->Maintain();
126 return tmp;
127 }
128 void PrintTree(Node* root,int deep){
129 for(int i=0;i<deep;i++)
130 fputc(' ',stderr);
131 if(root==NULL){
132 fprintf(stderr, "(==============================)\n");
133 return;
134 }
135 fprintf(stderr, "(root=0x%X,key=%d,min=%d,size=%d,minp=%d)\n", root,root->key(),root->min(),root->size(),root->minp());
136 PrintTree(root->lch,deep+1);
137 PrintTree(root->rch,deep+1);
138 }
139 public:
140 SplayTree(){
141 this->root=NULL;
142 }
143 void Import(const std::vector<pr>& v){
144 delete this->root;
145 this->root=new Node(std::make_pair(INF,INF));
146 this->root->rch=new Node(std::make_pair(INF,INF));
147 this->root->rch->prt=this->root;
148 this->root->rch->lch=Build(v,0,v.size()-1);
149 this->root->rch->lch->prt=this->root->rch;
150 this->root->rch->Maintain();
151 this->root->Maintain();
152 }
153 void Reverse(int l,int r){
154 this->Splay(this->Kth(l-1));
155 this->Splay(this->Kth(r+1),this->root);
156 this->root->rch->lch->Flip();
157 }
158 Node* Kth(int pos){
159 pos++;
160 Node* root=this->root;
161 while(root!=NULL){
162 root->PushDown();
163 int k=root->lch->size()+1;
164 if(pos<k)
165 root=root->lch;
166 else if(pos==k)
167 return root;
168 else{
169 pos-=k;
170 root=root->rch;
171 }
172 }
173 return NULL;
174 }
175 void Modify(int pos,pr d){
176 Node* tmp=this->Kth(pos);
177 tmp->k=d;
178 while(tmp!=NULL){
179 tmp->Maintain();
180 tmp=tmp->prt;
181 }
182 }
183 int MinPos(){
184 int ans=0;
185 Node* root=this->root;
186 while(root->minp()!=-1){
187 root->PushDown();
188 if(root->minp()){
189 ans+=root->lch->size()+1;
190 root=root->rch;
191 }
192 else
193 root=root->lch;
194 }
195 ans+=root->lch->size()+1;
196 return ans-1;
197 }
198 void Print(){
199 this->PrintTree(this->root,0);
200 }
201 };
202
203 int main(){
204 int n,tmp;
205 freopen("roboticsort.in","r",stdin);
206 freopen("roboticsort.out","w",stdout);
207 SplayTree* t=new SplayTree();
208 std::vector<pr> v;
209 scanf("%d",&n);
210 while(n!=0){
211 v.clear();
212 for(int i=0;i<n;i++){
213 scanf("%d",&tmp);
214 v.push_back(std::make_pair(tmp,i));
215 }
216 t->Import(v);
217 for(int i=1;i<=n;i++){
218 int p=t->MinPos();
219 printf("%d ",p);
220 t->Reverse(i,p);
221 t->Modify(i,std::make_pair(INF,i));
222 }
223 putchar('\n');
224 scanf("%d",&n);
225 }
226 return 0;
227 }

来源:http://www.cnblogs.com/rvalue/p/7278902.html